2.2.15 Матричные игры и линейное программирование

Основные понятия теории игр содержатся в разделе 2.2.14.

Стратегии игры двух игроков определяются платежной матрицей вида

, (2.15.1)

где – выигрыш игрока при -ой стратегии, при стратегии его противника.

Определяются два оптимальных плана в смешанных стратегиях

; ,

где и вероятности применения чистых стратегий игроками и .

Неизвестна цена игры , стратегия должна обеспечить выигрыш, не меньше чем при любом поведении противника.

Чтобы цена была , надо чтобы элементы платежной матрицы были неотрицательны. Это можно достигнуть, прибавив к элементам матрицы одну и ту же величину , при этом цена игры увеличится на , но решение при этом не меняется.

Предположим, что игрок применяет оптимальную стратегию, средний выигрыш при применении противником своей чистой стратегии

, . (2.15.2)

Стратегия оптимальная при любом поведении противника обеспечивает выигрыш не меньше чем , отсюда условия

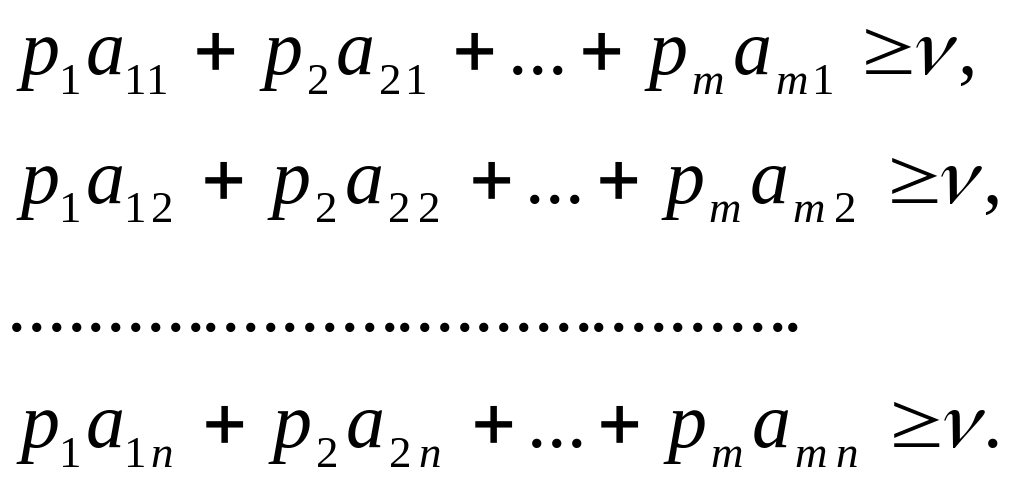(2.15.3)

Разделим неравенства на и обозначим

, ,… , . (2.15.4)

В результате получим ограничения

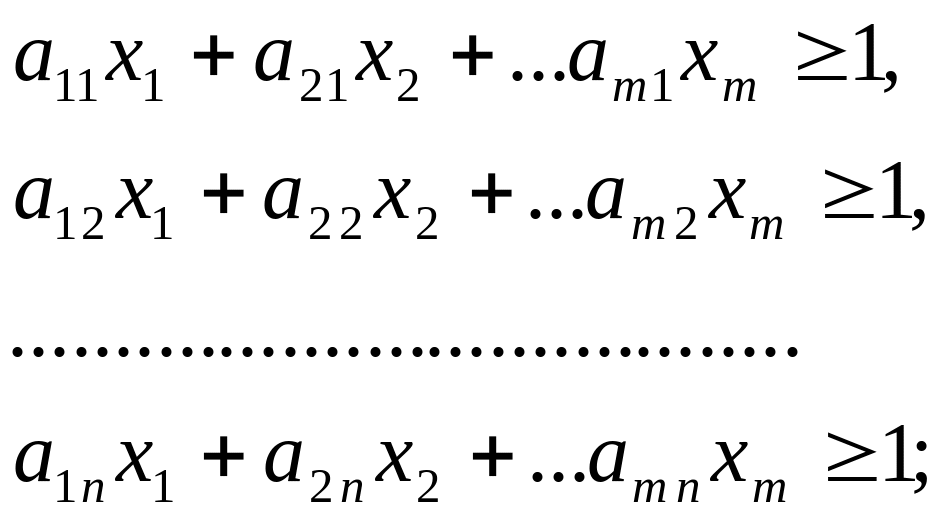(2.15.4)

и так как , то дополнительно

. (2.15.5)

Поскольку выигрыш игрока желателен максимальным, то должна принимать минимальное значение, тогда функция цели примет вид

. (2.15.6)

Задача (2.15.4), (2.15.6) является задачей линейного программирования. Для игрока может быть построена двойственная задача минимизации выигрыша (проигрыша), т.е. максимизации .

Обозначив

; ; … , (2.15.7)

получим задачу

, (2.15.8)

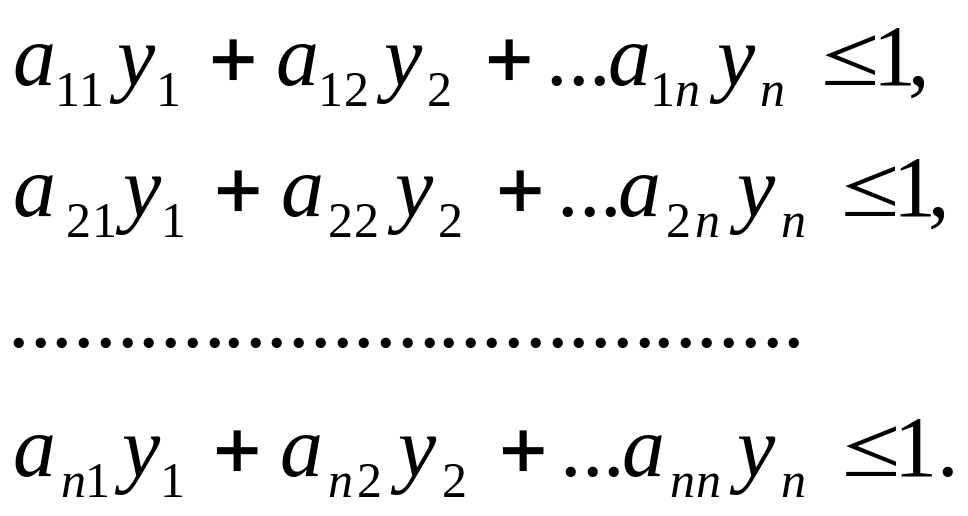(2.15.9)

Задача 2.2.15.1. Сторона располагает тремя видами вооружения , сторона тремя видами помех . Вероятность решения боевой задачи стороной задана матрицей

	0,8	0,2	0,4
	0,4	0,5	0,6
	0,1	0,7	0,3

Сторона стремится воспрепятствовать боевой задачи. Найти решение задачи, т.е. вероятности .

Решение.

Освободимся от дроби, для чего элементы матрицы умножим на 10

.

Цена игры получит значение .

Задача для игрока примет вид

Для перехода к стандартной задаче линейного программирования возможна смена знаков, и применение симплекс-метода уточнения оценок (с допуском отрицательных элементов в столбце свободных членов).

Для использования метода последовательного улучшения плана можно рассмотреть двойственную задачу для игрока .

Канонический вид ее приведен ниже с добавлением переменных .

,

Исходная таблица имеет вид

Таблица 15.1

			0	1	1	1	1	1	1
№
1		1	1		2	4	1	0	0
2		1	1	4	5	6	0	1	0
3		1	1	1	7	3	0	0	1
			0	–1	–1	–1

В качестве разрешающего столбца применим первый с разрешающим элементом 8, тогда выводится из базиса и заменяется в базисе .

Таблица 15.2

			0	1	1	1	1	1	1
№
1		1					1	0	0
2		1		–			0	1	0
3		1		–			0	0	1
					–	–

За разрешающий столбец принимаем при = – , в базис вводится , из базиса выводится .

Новая симплексная таблица получит вид (15.3).

Таблица 15.3

			0	1	1	1	1	1	1
№
1		1			–		1	0	0
2		1		–			0	1	0
3		1			–		0	0	1

Поскольку все неотрицательны, получен оптимальный план

.

.

По значению в последней таблице можно найти решение двойственной задачи

.