1.7. Эдс обмотки, вращающейся в пульсирующем магнитном поле
Рассмотрим общий случай вращения ротора с обмоткой в пульсирующем магнитном поле. Воспользуемся рис.1.4. Как и в предыдущем случае, к обмотке статора подведено переменное синусоидальное напряжение = и в этой обмотке проходит переменный ток = , создающий пульсирующий вдоль оси обмотки статора магнитный поток, определяемый выражением (1.33)
,
в котором следует принять в соответствии с (1.11)
, (1.42)
где
определяет угловую скорость вращения
ротора. При этом условии магнитный поток
через обмотку ротора по выражению (1.33)
будет функцией двух переменных: углового
положения ротора
и непосредственно времени
,
т. е. мгновенное значение магнитного
потока
при фиксированном
определяется собственным изменением
магнитного потока во времени, а в момент
времени
зависит от углового положения ротора
.
В соответствии с этим получим
(1.43)
Функция φ(t) является, во-первых, функцией двух переменных и t, и, во-вторых, представляет собой сложную функцию с промежуточной переменной . Это обстоятельство должно учитываться при вычислении производной от функции φ(t) по времени.
Мгновенное значение ЭДС, индуцированной в обмотке ротора, в соответствии с выражением (1.9)
или с учётом (1.43)
(1.44)
Составим выражение для производной в выражении (1.44)
Первое слагаемое в правой части определяет ЭДС вращения, а второе – трансформаторную ЭДС, и тогда выражение (1.44) примет вид
;
, (1.45)
. (1.46)
В этих выражениях магнитный поток φ(t) при синусоидальном напряжении на обмотке статора
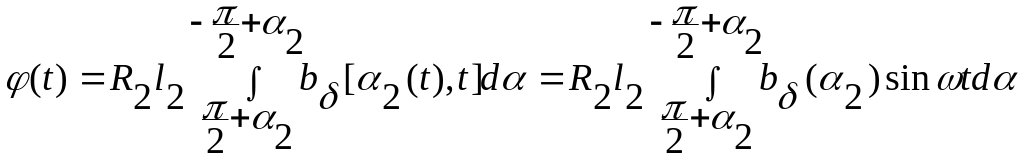
Вычислим ЭДС вращения и трансформаторную для частного случая гармонического распределения магнитной индукции в воздушном зазоре
,
и тогда мгновенное значение магнитного потока
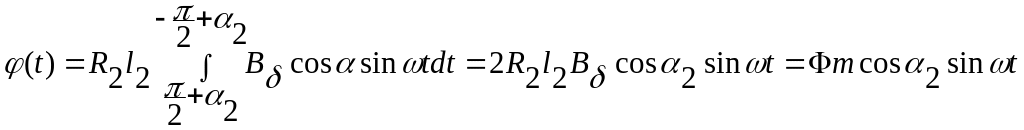(1.47)
Подставляя (1.47) в (1.45) и (1.46), получим
(1.48)
(1.49)
Из этих выражений следует, что ЭДС вращения находится в фазе с магнитным потоком обмотки статора и опережает трансформаторную ЭДС во времени на угол π/2. ЭДС вращения проходит через ноль в момент времени, когда оси обмоток совпадают, при этом трансформаторная ЭДС достигает наибольшего значения.
Таким образом, при вращении ротора в пульсирующем магнитном поле в его обмотке индуцируются две переменные во времени синусоидальные ЭДС, имеющие в общем случае разные амплитуды, частоты и фазы.
1.8. Знак «минус» в выражении для эдс и его физический смысл.
В выражении для мгновенного значения ЭДС перед производной стоит знак «минус». Есть работы, авторы которых полагают, что этот минус принят для удобства и сам по себе лишён какого-либо физического смысла, тем более, что на значение ЭДС этот знак никак не влияет.
Рассмотрим прямоугольный контур, вращающийся в плоско параллельном магнитном поле с постоянной угловой скоростью . На рис.1.5а и 1.5б представлены положения контура относительно этого магнитного поля, соответствующие двум моментам времени.
ЭДС вращения
,
индуцированная в контуре, создаёт в
этом контуре ток
,
находящийся в фазе с ЭДC
(если не учитывать индуктивное
сопротивление контура). Этот ток, в свою
очередь, образует магнитный поток
,
направление силовых линий которого
определяется по правилу буравчика.
В
соответствии с рис.1.5а
дальнейшее вращение контура сопровождается
возрастанием ЭДС
и тока
и уменьшением внешнего магнитного
потока через контур
,
но зато возрастает собственный магнитный
поток контура
,
имеющий в нём то же самое направление,
что и магнитный поток
.
Это значит, что собственный поток контура
стремится
сохранить значение результирующего
магнитного потока в контуре. На рис.1.5.б,
наоборот, дальнейшее вращение витка
приводит к увеличению внешнего потока
через контур. Но при этом его собственный
магнитный поток
оказывается в противофазе с
,
и препятствует его возрастанию. На
основании этого можно заключить, что
собственный поток контура стремится
всегда обеспечить постоянство
результирующего потокосцепления
контура.
Таким образом, правило правой руки, определяющее направление ЭДС вращения, оказывается согласованным с правилом Ленца, по которому определяется направление трансформаторной ЭДС. Физической основой этих двух правил является принцип сохранения постоянства потокосцепления контура.
На рис.1.6 а,б
приведены по два контура 1 и 2. Внешний
контур 1 является источником магнитного
поля. В контуре 1 действует ЭДС
и проходит ток
.
Направления
и
в контурах 1 условно примем за положительные.
Ток
создаёт магнитный поле, в котором
расположены контура 2, в плоскости
перпендикулярной силовым линиям
магнитного поля.
Предположим, что (рис.1.6.а) магнитный поток через контур 2 начинает возрастать (рис.1.6.а), и тогда в этом контуре будет индуцироваться ЭДС, определяемая в общем случае выражением
Так как по
условию магнитный поток через контур
2 возрастает, то производная будет
положительна, а индуцированная в контуре
ЭДС
будет отрицательна, т.е. она будет
находится в противофазе с ЭДС
контура 1 и соответственно ток
контура 2 будет в противофазе с током
контура 1,
что согласуется с принципом Ленца.
Силовые линии собственного магнитного
поля контура 2 внутри контура находятся
в противофазе с внешним магнитным полем,
препятствуя его увеличению через контур
2, и обеспечивая тем самым постоянство
потокосцепления контура 2. На рис.1.6.б
приведён альтернативный вариант, когда
внешний магнитный поток через контур
2 начинает уменьшаться. Тогда производная
будет отрицательной, а ЭДС
условно положительной, т.е. она должна
иметь то же самое направление, что и ЭДС
.
Ток
в контуре 2 создаёт свой собственный
магнитный поток, находящийся внутри
контура в фазе с внешним магнитным
полем, препятствуя тем самым его
уменьшению в полном соответствии с
принципом Ленца. При этом также
обеспечивается принцип сохранения
постоянства потокосцепления контура.
Предположим, что ЭДС контура определяется выражением
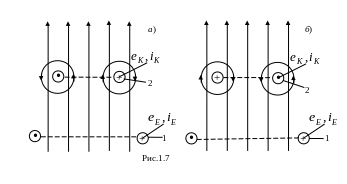
Пусть магнитный поток через контур 2 возрастает (рис.1.7 а), тогда ЭДС контура 2 будет положительной, так как производная положительна, т.е. ЭДС и токи в контурах 1 и 2 имеют одинаковые направления. Собственный магнитный поток контура 2 внутри контура складывается с внешним потоком, усиливая его, что будет сопровождаться дальнейшим увеличением ЭДС контура 2, тока в нём с последующим усилением магнитного потока и т.д. И через короткий промежуток времени магнитная индукция в зоне расположения контура 2 достигнет бесконечно большого значения, что теоретически невозможно, так как этому будет соответствовать бесконечно большая энергия.
Теперь предположим, что магнитный поток через контур 2 уменьшается (рис.1.7 б), обуславливая уменьшение ЭДС и так как производная <0, то и ЭДС будет также отрицательна и находится в противофазе с ЭДС . Собственный поток контура 2 находится в противофазе с убывающим внешним магнитным потоком, дополнительно его уменьшая с последующим уменьшением ЭДС контура 2. Через короткий промежуток времени поток в контуре окажется равным нулю и процесс наведения ЭДС в контуре 2 прекратится.
Из изложенного следует, что в замкнутом контуре ЭДС индуцируется только в том случае, когда внешний и собственный магнитные потоки контура меняются в противоположных направлениях, обеспечивая постоянство потокосцепления контура, что возможно лишь при наличии знака «минус» перед производной в выражении для ЭДС.