1.6. Трансформаторная эдс
Подведём к обмотке
статора переменное синусоидальное
напряжение
=
с действующим значением
,
круговой частотой
=
и начальной фазой
.
Это напряжение создаст в обмотке статора
переменный ток
=
,
отстающий от напряжения
на угол
из-за индуктивности обмотки статора.
Ток
будет создавать переменный, пульсирующий
вдоль оси обмотки статора, магнитный
поток
, (1.31)
Амплитуда этого магнитного потока определяется выражением (1.28).
Магнитная индукция
в воздушном зазоре в данном случае
будет функцией двух переменных координаты
и времени
(во времени магнитная индукция
будет
изменяться по тому же закону, что и ток
в обмотке статора
)
и тогда
(1.32)
При произвольном угловом положении обмотки ротора относительно обмотки статора мгновенное значение магнитного потока взаимной индукции обмотки ротора с обмоткой статора будет определяться выражением аналогичным (1.10)
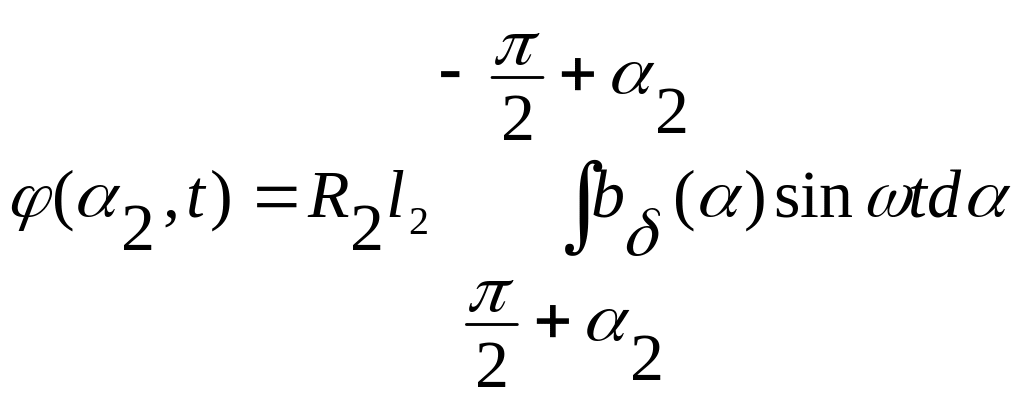(1.33)
Но в данном случае мгновенное значение магнитного потока через обмотку ротора зависит не только от углового положения ротора , но и от времени t. Так как интегрирование выполняется по координате , то можно вынести за знак интеграла и, вводя в рассмотрение величину магнитного потока
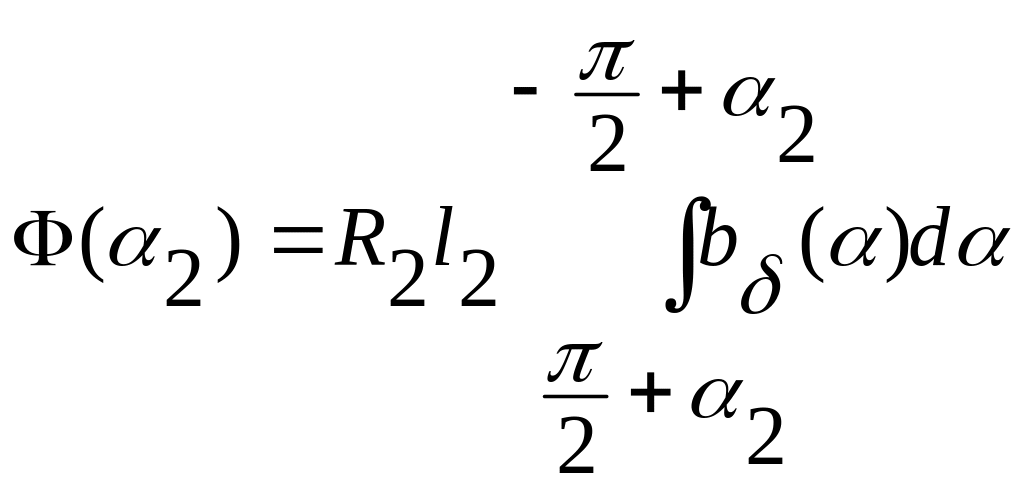, (1.34)
определяющую магнитный поток через обмотку ротора при его фиксированном положении, запишем выражение (1.33) в следующем виде
(1.35)
Предположим, что
ротор неподвижен (
=
0). Но так как переменный ток в обмотке
статора создаёт пульсирующий магнитный
поток, то и при неподвижном роторе
магнитный поток через обмотку ротора
будет меняться во времени. В результате
на основании закона электромагнитной
индукции пульсирующий магнитный поток
будет
создавать в обмотке неподвижного ротора
ЭДС
.
Мгновенное значение этой ЭДС формально
определяется выражением
(1.36)
При неподвижном
роторе
=
const
значение магнитного потока
будет также постоянным и тогда с учётом
(1.35) выражение (1.36) примет вид
(1.37)
Так как данная ЭДС обусловлена собственным изменением во времени магнитного потока, пронизывающего обмотку ротора, то она называется трансформаторной. Из сравнения выражений (1.35) и (1.37) следует, что трансформаторная ЭДС отстаёт от создавшего её магнитного потока на угол . Направление трансформаторной ЭДС определяется правилом Ленца.
Запишем выражение (1.37) в виде
(1.38)
(1.39)
Из выражения (1.38) видно, что форма кривой трансформаторной ЭДС определяется законом изменения напряжения на обмотке статора и не зависит от закона распределения магнитной индукции в воздушном зазоре.
Величина
определяет
действующее значение трансформаторной
ЭДС. Действующее значение трансформаторной
ЭДС пропорционально частоте тока в
обмотке статора
,
числу витков обмотки ротора
и значениию магнитного потока через
обмотку ротора
.
Магнитный поток
имеет наибольшее значение при
=
0, т.е. при совпадении осей обмоток статора
и ротора и при этом условии трансформаторная
ЭДС в соответствии с выражением (1.38)
достигает максимального значения. При
=
,
когда оси обмоток взаимно перпендикулярны,
магнитный поток
=
и соответственно трансформаторная ЭДС
также равна нулю. Особенностью
трансформаторной ЭДС является то, что
её значение не зависит от закона
распределения магнитной индукции в
зоне расположения обмотки ротора.
Рассмотрим частный случай гармонического распределения магнитной индукции в воздушном зазоре по выражению (1.22)
,
Тогда магнитный поток через обмотку ротора в соответствии с выражением (1.34)
=
=
=
=
(1.40)
Следовательно, плавно меняя угол поворота ротора, можно регулировать значение трансформаторной ЭДС в обмотке ротора. При совпадении осей обмоток статора и ротора ( = ) действующее значение трансформаторной ЭДС определяется выражением
(1.41)
Из сравнения выражений (1.29) и (1.41) видно, что формально они одинаковы. Но в ЭДС вращения частота определяется скоростью вращения ротора, а в трансформаторной ЭДС частота является частотой напряжения на обмотке статора.