2.9.3. Скорость вращения первой гармоники мдс

трёхфазной обмотки статора

Первая гармоника МДС многофазной обмотки статора вращается относительно расточки статора с некоторой угловой скоростью ω₁. Определим факторы, влияющие на значение даной скорости. Для этого воспользуемся рис. 2.14, на котором представлена первая гармоника МДС многофазной обмотки статора .

Особенностью бегущей волны является постоянство величины любой её ординаты в произвольный момент времени t, т. е. бегущая волна сохраняет свою форму при перемещении. Мгновенное значение первой гармоники МДС многофазной обмотки статора определяется выражением

(2.50)

Выразим угловую координату через линейное перемещение x по окружности расточки статора

_, (2.51)

где представляет собой полюсное деление статора

(2.52)

Тогда с учётом (2.51) выражение (2.50) примет вид

Постоянство ординаты волны возможно при условии

(2.53)

Продифференцировав по времени левую и правую части выражения (2.53), получим

(2.54)

Производная представляет собой линейную скорость перемещения волны , т.е. = и тогда из выражения (2.54) получим

= (2.55)

В свою очередь, линейную скорость ( в метрах в секунду) можно представить через скорость вращения (в оборотах в минуту):

= (2.56)

Подставляя (2.56) в (2.55), получим после преобразований

(2.57)

Имея в виду выражение (2.52) и ω = 2πf₁ преобразуем (2.57)

(2.58)

Выражение (2.58) определяет скорость вращения первой гармоники МДС многофазной обмотки статора, и эта скорость называется синхронной. Она пропорциональна частоте тока в обмотке статора и обратно пропорциональна числу пар полюсов p машины.

2.10. Мдс обмотки возбуждения неявнополюсной синхронной машины

Конструктивная схема синхронной неявнополюсной машины представлена на рис. 2.15. Воздушный зазор в машинах этого типа равномерный. Для того чтобы приблизить форму кривой магнитного поля в воздушном зазоре к синусоидальной, обмотка возбуждения ОВ, расположенная на роторе, на каждом полюсном делении выполняется распределённой и размещается в 8–20 пазах. Угол определяет дугу, соответствующую обмотанной части ротора в пределах полюсного делении. Постоянный ток , проходя по обмотке возбуждения, создаёт поток возбуждения , силовые линии которого, дважды пересекая воздушный зазор , замыкаются по сердечнику пакета стали статора.

Кривая 1 на рис. 2.16 представляет собой МДС распределённой обмотки возбуждения. Эта МДС построена при учёте конечной ширины проводников обмотки возбуждения.

В соответствии с выражением (2.41) при равномерном воздушном зазоре кривая распределения магнитной индукции поля возбуждения будет повторять форму кривой, создавшей её МДС. И тогда можно рассматривать как амплитуду действительной кривой магнитной индукции в воздушном зазоре. Величина характеризует амплитуду первой гармоники 2 магнитной индукции, полученной разложением в ряд Фурье кривой 1.

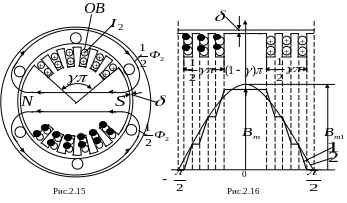
Как видно из рис. 2.16, при надлежащем выборе коэффициента действительная кривая 1 магнитной индукции в воздушном зазоре мало отличается от её первой гармоники 2.

При гармоническом анализе кривой МДС распределённой обмотки возбуждения ротора ОВ действительная ступенчатая кривая МДС 1 на рис. 2.16 заменяется равнобокой трапецией (кривая на рис. 2.17). Высота этой трапеции принимается равной высоте действительной ступенчатой кривой МДС на рис. 2.16, и при этом верхнее основание такой трапеции будет равно , а нижнее – , т. е. полюсному делению ротора в электрических радианах.

Трапецеидальную кривую на рис.17.7 обозначим через . При равномерном воздушном зазоре = = сonst магнитная индукция в любой точке на поверхности статора будет пропорциональна МДС , действующей в этой точке.

Поэтому трапецеидальную кривую на рис. 2.17 можно рассматривать одновременно как кривую распределения магнитной индукции поля возбуждения в воздушном зазоре, а кривую – как её первую гармонику с амплитудой .

Начало координат по окружности ротора выберем на оси большого зубца 3. Функция , характеризующая распределение магнитной индукции поля возбуждения в воздушном зазоре по окружности ротора (расточки

статора), является знакопеременной периодической с периодом , чётной

о тносительно выбранного начала координат и симметричной относительно оси ординат. При этих условиях функция будет содержать только косинусы нечётных порядков = , k=1, 2, 3,… и при разложении её в ряд Фурье примет вид

= ,

где амплитуда ой гармоники магнитной индукции

=

= (2.59)

Первый интеграл в фигурных скобках вычисляется достаточно просто

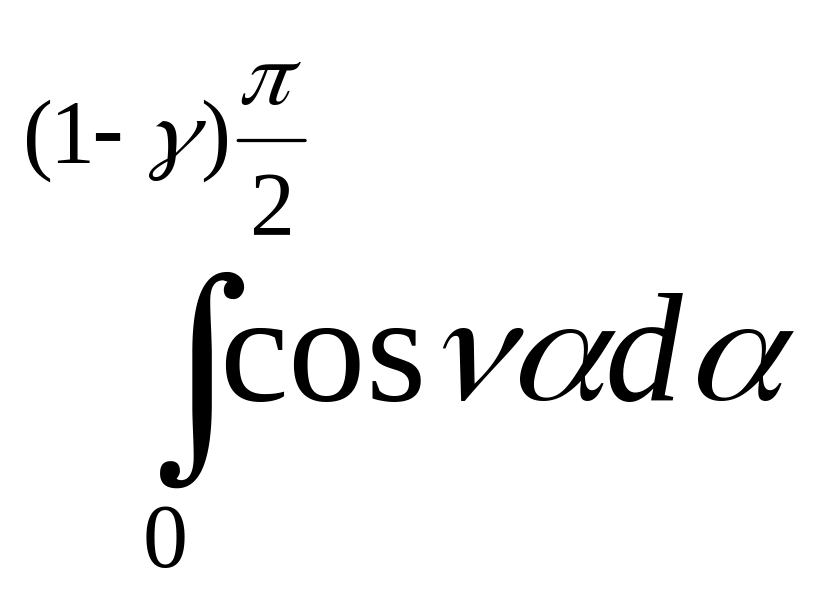= = (2.60)

Второй интеграл в фигурных скобках вычисляется методом интегрирования по частям

= – + (2.61)

Подставляя (2.60) и (2.61) в (2.59), получим

= (2.62)

Отсюда видно, что с увеличением порядка гармоники её амплитуда убывает обратно пропорционально квадрату порядка гармоники, т. е., например, амплитуда седьмой гармоники при > 0,5. Если принять =2/3, то = = 0, т.е. при указанном значении третья гармоника будет отсутствовать. Аналогично, при = 4/5 и = 5 = = 0 и, следовательно, отсутствует пятая гармоника. Отсюда получаем рекомендации по выбору значения коэффициента . При 0,67 0,80 третья и пятая гармоники в значительной мере ослаблены, а гармоники более высоких порядков пренебрежимо малы и действительная кривая магнитной индукции поля возбуждения в воздушном зазоре оказывается практически синусоидальной.

Приняв в (2.62) = 1, составим отношение

= ,

которое обозначим через k_f , и тогда

k_f = = (2.63)

Для синхронной неявнополюсной машины k_f = 0.965–1,065 при 0,67 0,80.