Лекции по матану 3-ий семестр / Лекции №13 - №15

Лекция 13

Определение 15. (полного метрического пространства)

Линейное пространство с введением в нем скалярное произведение называется полным, если сходящаяся последовательность

в нем сходится к

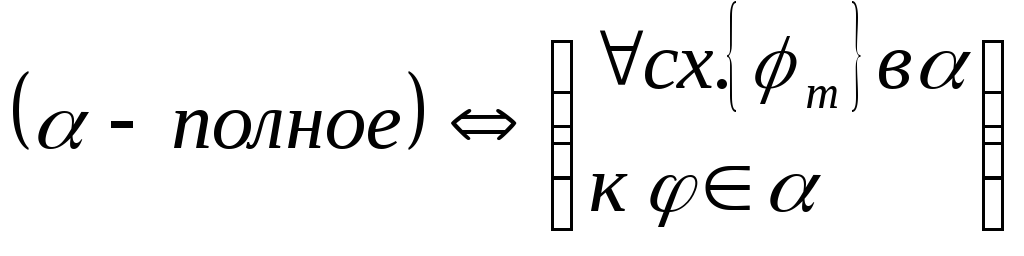
Примеры:

- неполное

(пространство непрерывной функции на

пример последовательности непрерывной функции , которая сходится к функции

Определение 16. (Гильбертово пространство)

Полное линейное пространство со скалярным произведением

- Гильбертово пространство (непрерывные, обобщенные функции)

- вводится так же как в

- интеграл Лебега (сходящаяся)

Тема 4. Ряды Фурье в гильбертовом пространстве

- гильбертово пространство

Определение 17. (ортогональная система функций)

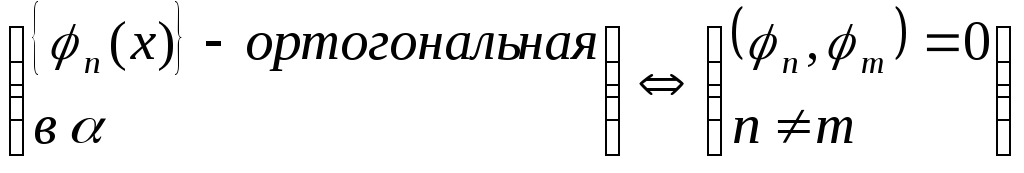
Определение 18. (Ортонормир. система функций)

Пример1:

Тригонометрическая система функций

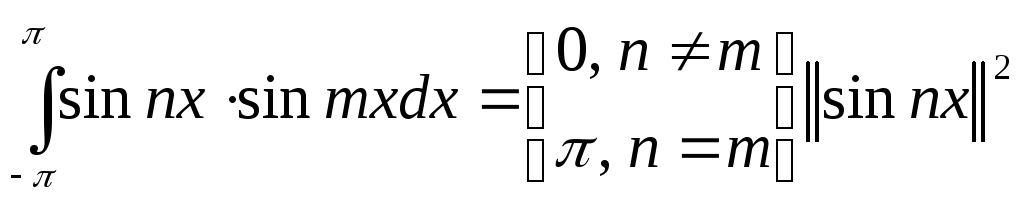
- пронормировали ортонорм. Система

Пример 2.

ортогональна в

Определение 19. (полной системы функций)

- полная в , если элемент из этого пространства

можно представить в виде бесконечной суммы

Определение 20. (обобщенного ряда Фурье)

- ортогональная система функций – линейна независима

- гильбертово пространство

- ортогональная система

(1)

умножим левую и правую часть на при =0

(2) коэффициент Фурье

1. – обобщенный ряд Фурье

Замечание. Если - тригонометрическая система, то получим тригонометрический ряд Фурье.

-

Определение 21. (частное суммы ряда Фурье)

Называется конечная сумма ; где находится на (2) (3)

В

В - сходимость в смысле среднеквадратичного

Тема 4. ( о минимальном свойстве коэффициента Фурье)

Наилучшее приближение элемента в смысле метрики пространства дают частное суммы обобщенного ряда Фурье (3), т.е.

Следствия: (неравенство Бесселя)

В (4) перейдем к : (5)

Если можно составить ряд Фурье.

(6)

Теорема 5. ( о равенстве Парсеваля)

Чтобы (6) сходилось к функции должно выполниться равенство Парсеваля

(7)

Геометрическая интерпретация

ортонорм.

Из (7) (8)

n=2 теорема Пифагора на беск. Неравенстве

Теорема 6.

полная в гильбертовом пространстве

Определение 22. (замкнутые системы)

- замкнутая в , если элемента из

Теорема 7. В гильбертовом пространстве ортогональная ситема функций замкнута, когда она полна в

Теорема 8. Тригонометрическая система функций

- полная и замкнутая в

(9)

- по формулам (2).

Равенство Парсеваля:

(7) (10)

Пример:

1) получить разложение в ряд Фурье, продолжив ее нечетно на

установить виды сходимости частного сумм ряда данной функции

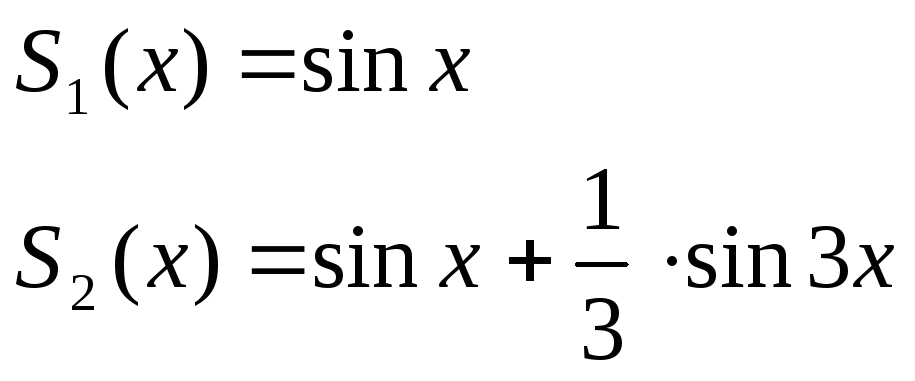
Виды сходимости

1. равномерности нет! Получаются разрывы

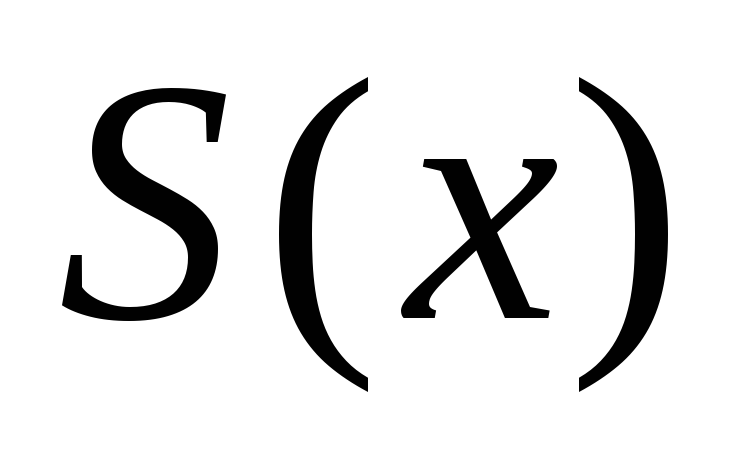
2. поточечная сходимость есть к S(x) на

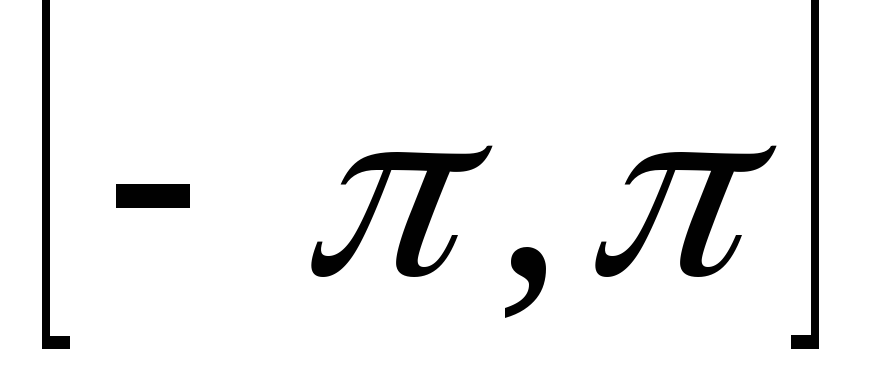
вне: к периодическому продолжению S(x)

3)сходимость в среднем да!

Лекция 14

Замечание 1:

Исп-л ряда Фурье можно проссумировать числовой ряд

при

Использованием равенства Парсевалл также находится ряда

Замечание 2: О равномерности сходимости рядов Фурье.

Равномерная сходимость => пототечная сходимость для установления сходимости надо знать:

Теорема 9. ( о равномерности сходимости)

Если функция периода непрерывна на всей числовой оси и имеет кусочно-непрерывную производную на периоде, то ее ряд Фурье сходится равномерно на всей числовой оси и сходится равномерно и на периоде тоже.

Замечание 3. ( о сходимости в среднем)

Теорема 10. ( о сходимости по норме обобщенного ряда Фурье)

- гильб. Сходится к этому элементу по норме пространства, т.е.

Следствие: ( о тригонометрическом ряде Фурье)

Тригонометрический ряд Фурье периодической функции сходится к ней «в среднем», т.е. в смысле среднего квадратичного

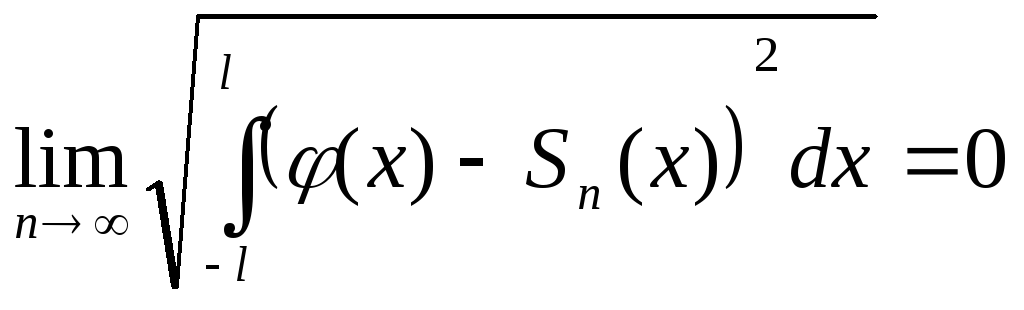Из сходимости «в среднем» поточечная.

Пусть изменим ее только в 2-х точках:

Окажется что ряд Фурье один и тот же. Он будет сходится «в среднем».

Поточечная будет сходиться к разным функциям.

Тема 5. Ряд Фурье в комплексной форме.

Дискретный спектр. Интеграл Фурье. Спектральная функция. Амплитудный и фазовый спектры cos и sin преобразования Фурье. Интеграл Фурье для четной и нечетной функции

(1)

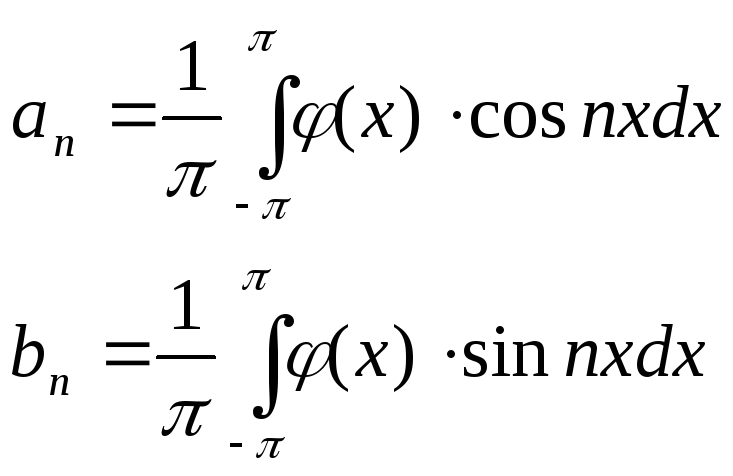
Используя формулу Эйлера (см. приложения степенного ряда) выпишем cosnx и sinnx с ее помощью:

(2)

(3)

подставим (2), (3) в (1) и приведя подобные, получим:

(4)

Обозначим (5)

Подставим (5) в (4):

(6) функция Фурье в комплексной форме

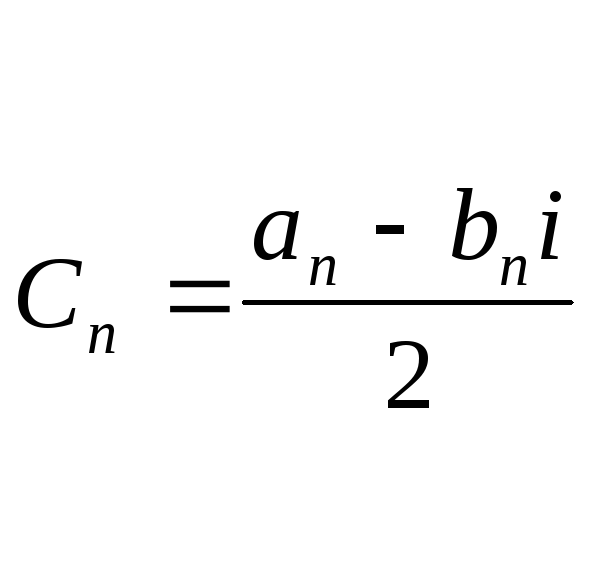(*) , используя формулу Эйлера,

= (7)

Определение 24. (дискретность спектра)

Коэффициент по (7) называется дискретным спектром.

Теорема 11. ( об интеграле Фурье)

Если функция не периодическая, но абсолютно интегральная,т.е.

- сходится, то

(8)

(9)

(10)

коэффициент называется коэффициентом Фурье.

Определение 25. – интеграл Фурье в вещ. Форме

Замена (1) у »n» непрерывность дискретная

(8), (9), (10) получаются из (1) и предыдущей темы предельным переходом.

Двойной интеграл в вещественной форме.

Если подставить (9) и (10) в (8) и используя тригонометрическую форму

получим двойной интеграл Фурье в вещественной форме.

(11)

Двойной интеграл в комплексной форме

(12)

Определение 26. (преобразования Фурье)

(13) называется прямым преобразованием Фурье

(14)

Определение 27. (спектральная функция)

Ф(у) – спектральная функция

Определение 28. (амплитудная и фазная спектра)

- амплитудный спектр

:Определение 29. (cos и sin преобразования Фурье)

(15)

(16)

Теорема 12. Преобразование Фурье четной функции = его cos-преобразованию (15)

Т.е. (17)

Доказательство:

Теорема 13. (преобразование Фурье от F неч = ее sin преобразованию, умноженному на (-i), т.е. (18)

Найти амплитуду спектра

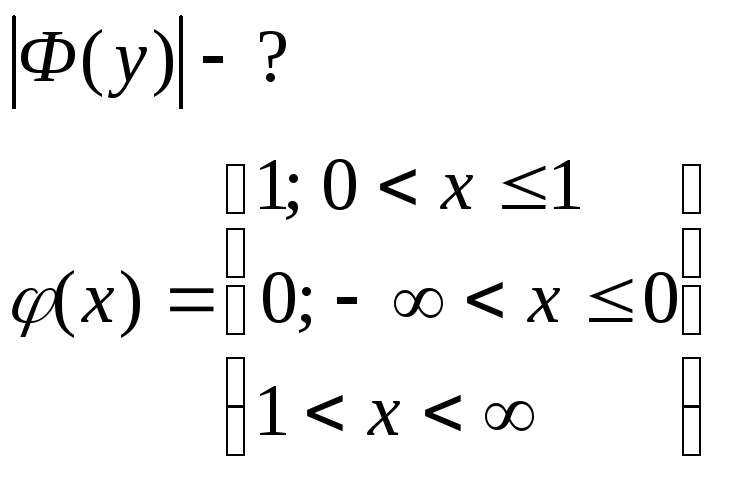
построив и ее спектр.

Замечание.

Большую роль в приложении играют обобщенные функции.

- функция (введена Полем Дираком)

единичная масса, сосредоточенная в 0.

(1) 2-й порядок

Определение 32. (линейные уравнения)

Уравнения – линейны, если искомая функция в 1-х степенях.

1. Волновое уравнение

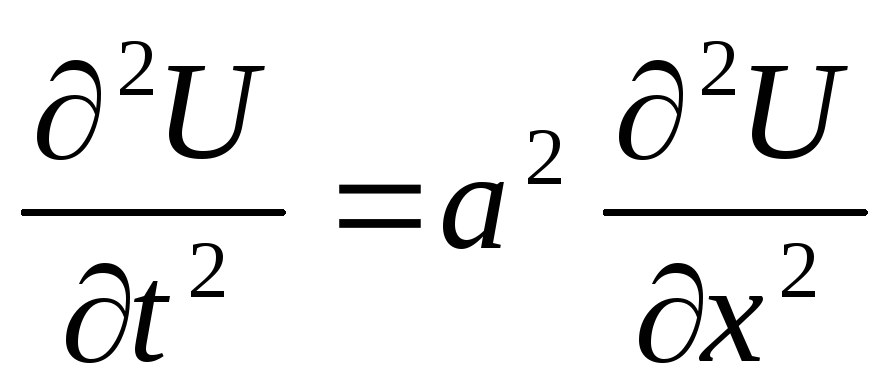
2. Теплопроводности

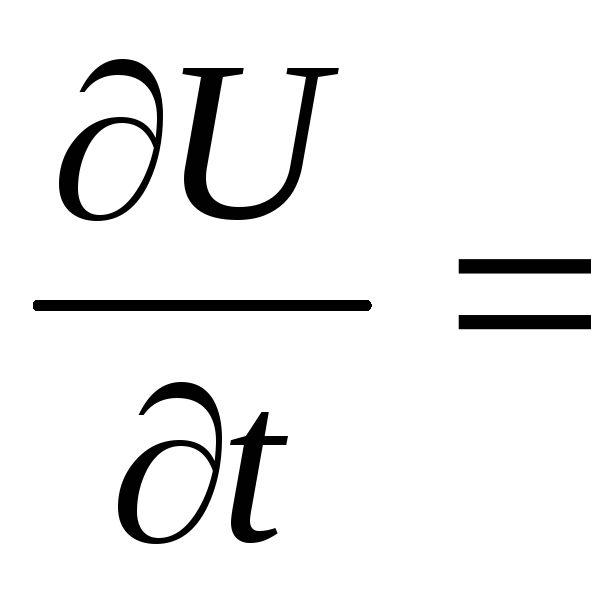
3. Лапласа

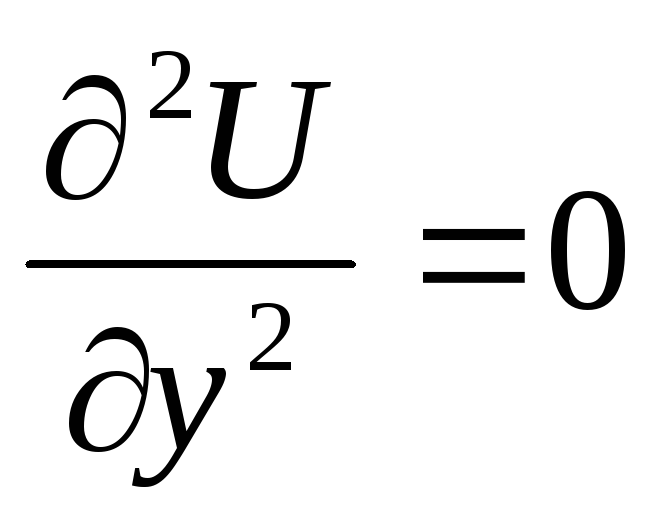
Гармонические функции

Определение 33. (решение уравнения в част. произв.)

Решение(1) называется удовлетворяет (1)

Лекция 15. Решение уравнения методом Фурье

(1)

краевые условия

(2)

- длина струны

концы струны закреплены

Начальные условия:

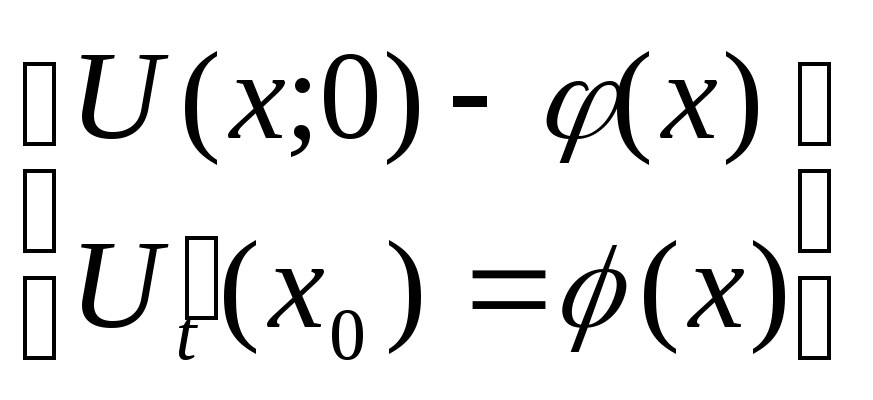а) -положение струны в начальный момент времени (3)

б) – начало скольжения струны