Лекции по матану 3-ий семестр / Лекции №5 - №8

Тема №6

Функциональные ряды

Опр.10 (функц. ряда )

∑U(x) (1), где U(x) имеет общую область определения X.

Пример: ∑(х)ⁿ = 1+х+х² +. . . + хⁿ+ …=∑(x)^n-1 , Х=(-∞,∞)

Пусть х=1/2

∑(1/2)^n-1 --геометрическая прогрессия q=1/2<1 , сходится

Пусть х=2:

∑2^n-1 – геометрическая прогрессия с q=2>1 –расходится.

В каждой конкретной точке х₀ функциональный превращается в числовой.

Опр.11 (точек сходимости и области сходимости функционального ряда)

Х=Х₀ , где ряд сходится(∑U(х₀)—сходится)(точка сходимости ф.р (∑U(х) ).

Совокупность т. Сходимости называется область сходимости(Е).

Чтобы Ряд ∑U(х)—сходился в Е  S_n(x)_n→∞S(x) , т.е. для любого ε→0 существует N(ε, х) > 0 такое что для любого n> N(ε, х) и данного х (пренадл Е) выполняется |S(x)- S_n(x)|<ε (2)

Т.е |r_n(x)|<ε (3)

Замечание : не всегда бесконечная сумма непрерывных функций будет функцией непрерывной.

Опр. 13( мажоранты)

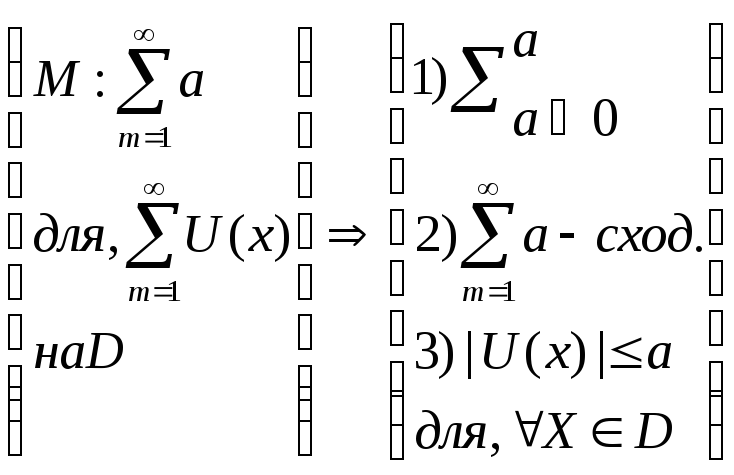
Т.16(достаточное условие Веерштрасса, равномерной и абсолютной сходимости)

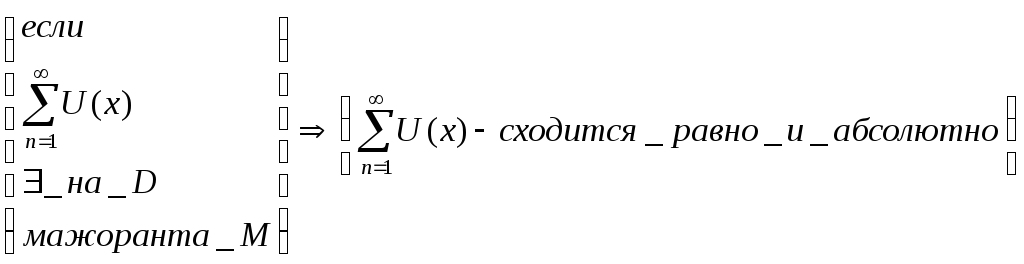
Док-во

1)абсолютная сходимость очевидна из 3) условия + допредельный признак сравнения  из сходимости большего следует сходимость меньшего.

2)

|r_n(x)|=|U_n+1 (x)+U_n+2(x)+....+ || U_n+1 (x)|+| U_n+2(x)|+...

По 3) условию М а_n+1 +a_n+2 = r_n --мажоранты

Тема№7 свойства равномерно сходящихся рядов: непрерывные суммы интегрирование и дифференцирование рядов.

Т.17(о непрерывности суммы)

Сумма равномерно сходящегося ряда непрерывных функций есть функция непрерывная.

Дано 1)

2)U_n(x)-непрерывна на D

Доказать , что S(х) непрерывна на D , т.е. х₀ ,х

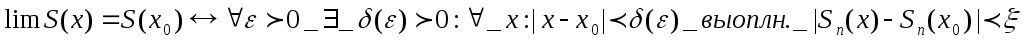
Док-во

1)U_n(x)-непрерывн. На D

2)

Замечание 1

Если сумма бесконечного ряда непрерывных функций окажется функцией разрывной , то данный ряд сходится к сумме не равномерно.(док-во от противного)

Т.18(об интегрировании функционального ряда)

Равномерно сходящийся ряд непрерывных функций на [a,b] можно почленно интегрировать на этом отрезке ,т.е.

Дано 1) равномерн. На [a,b]

2)U_n(x)-непрерывная функция на [a,b]

Доказать

Доказательство

Аналогично Т.17

Т.19(о дифференцировании функциональных рядов)

Дано 1)

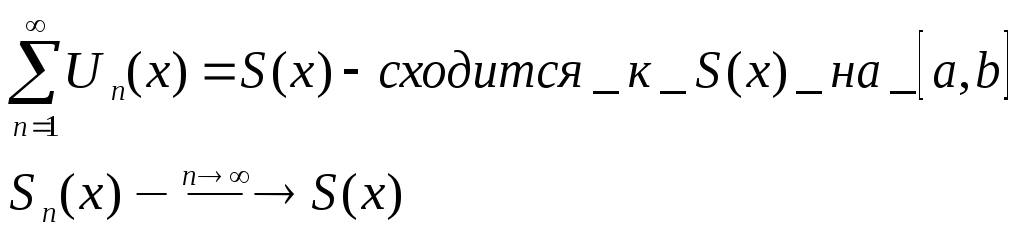
2)U_n(x) имеют непрерывные производные на [a,b]

3)

Тогда исходный ряд можно почленно дифференцировать

Замечание 2 в Т.18 (4) можно записать для любого отрезка [a,x] где

Док-во

Из (3)  (по Т.18)его можно интегрировать на любом отрезке

Тема степенные ряды

Опр. (действительного (вещественного) степенного ряда)

Х₀-центр ряда.

Опр. (комплексного степенного ряда)

Замечание. Ряды (3) и (4) всегда можно получить соответственно из рядов (1)и (2) следующими заменами

x-x₀=X

z-z₀=Z

замечание

вся теория функциональных рядов переносится и на их яркий представитель –степенные ряды.

Теорема Абеля

Формулировка для ряда (3)

Если ряд (3) сходится в т. Х₁ 0 ,то он:

1)абсолютно сходится в |x|<|x₁| (5)

2)равномерно сходится на отрезке |x|<r<| x₁| (6)

Док-во

1)абсолютная сход. т.к. ряд сходится в т. --- сходится числовой ряд  выполняется необходимый признак : она ограничена

6