Лекции по матану 3-ий семестр / Лекция №4

Лекция №4

Тема №5

Абсолютно и условно (не абсолютно) сходящиеся ряды. Их свойства.

Определение №8: - абсолютная сходимость

Чтобы (1) абсолютно сходился, необходимо достаточно, чтобы сходился (2)

Определение №9: - условная сходимость

Чтобы (1) сходился условно, необходимо и достаточно, чтобы:

1. сходился

2. расходился

Теорема №11: - Достаточное условие сходимости числовых рядов, или о взаимосвязи сходимости и абсолютной сходимости.

Если сходится абсолютно, то он и просто сходится.

Доказательство:

Т.к. (1) абсолютно сходится, то сходится , следовательно существует , следовательно возрастает, следовательно (3)

- частичные суммы ряда (2)

(4)

- частичные суммы, входящие в с “+”

- частичные суммы, входящие в с “-” (сумма их абсолютных значений)

(5)

Используя неравенство (3) и равенство(5) можно сделать вывод:

(6)

(7)

Из (6) и (7) следует, что и ограничены

возрастает, возрастает (по их сути), следовательно существует и существует

По равенству 4 вытекает существование - теорема доказана.

Примеры:

№1

ряд Лейбницкого типа S < 1

расходится, следовательно, для исходного ряда абсолютной сходимости нет, следовательно, ряд сходится условно или не абсолютно.

№2

- геометрическая прогрессия, q = 1/2 < 1, следовательно сходится, следовательно, исходный ряд сходится абсолютно.

Свойства абсолютно сходящихся рядов.

1. На абсолютно сходящиеся ряды распространяются все признаки сходящихся положительных рядов, например, Коши радикальный:

Если существует , то ряд = сходится, при q < 1

расходится, при q > 1

Примеры:

№1

- сходится абсолюьно.

1. Необходимый признак выполняется, т.к.

2. Проверка абсолютной сходимости

№2

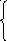= сходится абсолютно при

сходится условно при

расходится при

1) - сходится абсолютно, т.к.

- ряд Дирихле

2) - ряд Лейбницкого типа

3) - не выполняется необходимый признак

№3

- сходится абсолютно

- сходится

Замечание:

Из примеров виден алгоритм исследования произвольных числовых рядов на сходимость

Алгоритм:

1. Проверка необходимого признака (не выполняется – расходится, выполняется – к п. 2)

2. Проверка на абсолютную сходимость (если сходится абсолютно, то сходится и условно, если абсолютно не сходится, то к п.3)

3. Проверка условной сходимости (признак Лейбница и другие)

2) Сочетательное свойство

Теорема №12 – О сочетательном свойстве

Если абсолютно сходится, то для такого ряда сохраняется сочетательное свойство конечных сумм

Замечание 2:

На самом деле сочетательное свойство конечных сумм справедливо не только для абсолютно сходящихся рядов, но и для всех рядов.

3) Переместительное свойство

Теорема №13 – О переместительном свойстве абсолютно сходящихся рядов

Для абсолютно сходящихся рядов выполняется переместительное свойство конечных сумм, т.е.

Если , то

Замечание 3:

Это свойство справедливо только для абсолютно сходящихся рядов ( и для положительных рядов), а для условно сходящихся рядов, как будет показано позднее, это свойство не имеет места.

4) Перемножение абсолютно сходящихся радов

Теорема №14 – О произведении абсолютно сходящихся рядов

Пусть (8) сходится абсолютно, (9) сходится абсолютно, тогда так же сходится абсолютно и его сумма равна произведению сумм перемножаемых рядов

Замечание №4:

может быть составлен как угодно, лишь бы вошли все попарные произведения членов перемножаемых рядов.

Например:

Замечание 5:

Если ряды (8) и (9) сходятся не абсолютно, то в результате перемножения можно получить даже расходящийся ряд.

Например:

сходится условно;

сходится условно;

не стремится к 0, не выполняется необходимый признак, следовательно, ряд расходится.

Замечание 6:

Для условно сходящихся рядов переместительное свойство не имеет места.