Лекции по матану 3-ий семестр / Лекция №1

Лекция №1

1. Числовые ряды

2. Функциональные ряды

3. Степенные ряды (частный случай функциональных рядов)

4. Ряды Тейлора (частный случай степенных рядов)

5. Приложения степенных рядов

6. Ряды Фурье (частный случай функциональных рядов)

7. Тригонометрические ряды Фурье

8. Интеграл Фурье

9. Уравнения математической физики

Тема №1

Числовые ряды

или n = 1, 2…

- числовая последовательность действительных (комплексных) чисел

Выражение вида

называется числовым рядом (бесконечным числовым рядом)

- общий член ряда

Замечание 1

Бесконечная сумма бесконечно малых функций не всегда будет бесконечно малой (она может оказаться даже бесконечно большой)

Примеры рядов:

1) - геометрическая прогрессия

2) - частный случай геометрической прогрессии,

q=1/2

3) - гармонический ряд

4)

5)

Определение:

Частичная сумма ряда – сумма n первых членов ряда

Определение:

- сходящийся числовой ряд, если:

1. Существует конечный

2. S – сумма сходящегося ряда

Ряд расходится, если предел равен бесконечности или не существует

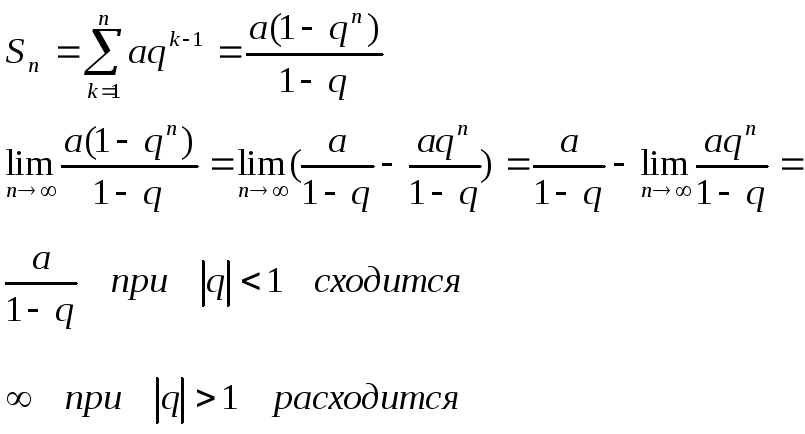
при q = 1; a + a + a + a …

при q = -1; a – a + a – a + …

0, n = 2k

a, n = 2k+1

Геометрическая прогрессия сходится при и расходится при

Из примеров (см. выше)

1. сходится, , S = 1/(1-q)

расходится при

2. q = ½, сходится

3. - гармонический ряд, расходится. Бесконечная сумма бесконечно малых является бесконечно большой

Доказательство:

Из этого неравенства получается следующие оценки:

4)

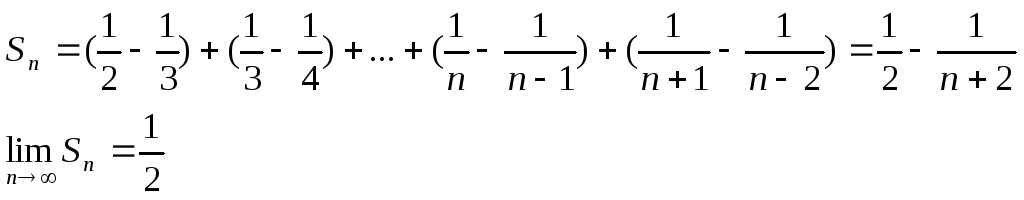
5) сводится к исследованию двух действительных рядов. Комплексный ряд сходится тогда и только тогда, когда сходятся оба действительных ряда и расходится, когда расходится хотя бы один.

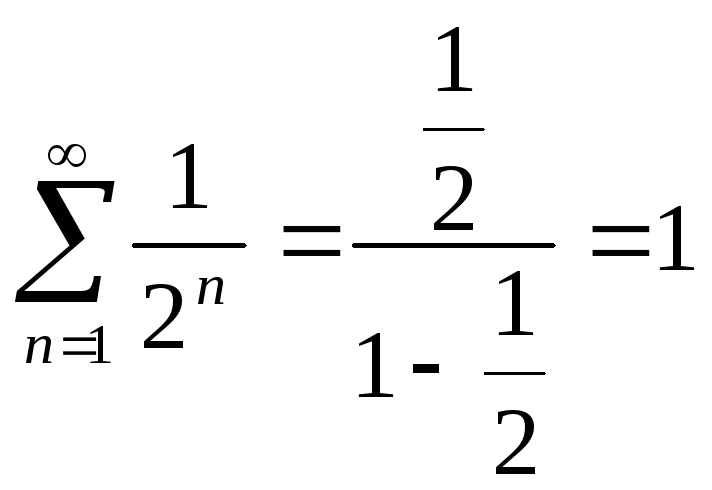
Тема №2

Свойства сходящихся числовых рядов

Теорема №1 – Необходимый признак сходимости числовых рядов

- сходится

Доказательство:

Из сходимости ряда следует:

Обратное неверно, как показывает пример гармонического ряда

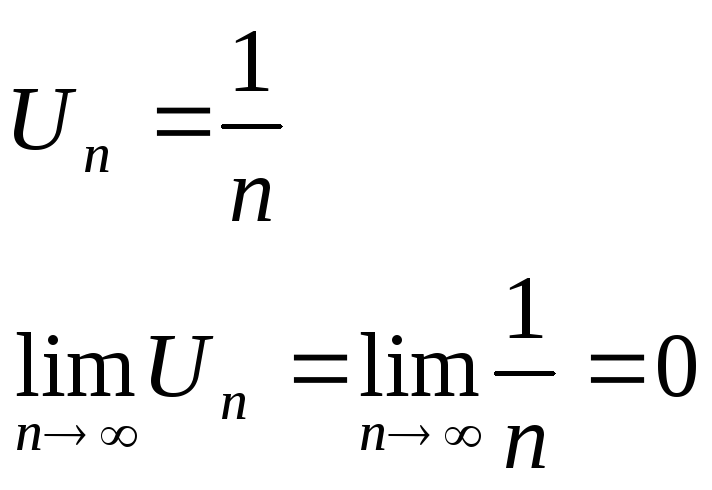
но ряд расходится.

Замечание №2

Если , то ряд расходится

Доказательство:

Предположим, что ряд сходится, но тогда по теореме №1 , а он ряд расходится.

Определение №4 – Остатка ряда

выражение такого вида называется остатком ряда.

Если ряд сходится, то

, - ошибка приближения.

Утверждение:

1. Остаток сходящегося ряда есть бесконечный сходящийся ряд

2. 

1-ое доказывается от противного, а 2-ое следует из того, что