2.2. Интегралы от неограниченных функций (II рода)
Если функция у = f ( x ) непрерывна в промежутке [a; b) и имеет разрыв 2-го рода («убегает» в бесконечность) при x = b, то несобственный интеграл от неограниченной функции определяется следующим образом:
.
Если предел справа существует, то несобственный интеграл II рода называется сходящимся, в противном случае – расходящимся.
Аналогично,
если функция у
= f
(
x
) терпит
бесконечный разрыв в точке x
= а, то
полагают
.
Если функция у
= f
(
x
) терпит разрыв
2-го рода во
внутренней точке с
[a;
b],
то несобственный интеграл II
рода определяется формулой
+
.
В этом случае интеграл называется
сходящимся,
если оба несобственных интеграла,
стоящих справа, сходятся.
Некоторые признаки сходимости и расходимости несобственных интегралов II рода
1.
Признак
сравнения.
Если на промежутке [a;
b)
функции f
(x)
и g
(x)
непрерывны, при х
= b
терпят разрыв 2-го рода и удовлетворяют
условию 0 ≤ f
(x)
≤ g
(x),
то из сходимости интеграла
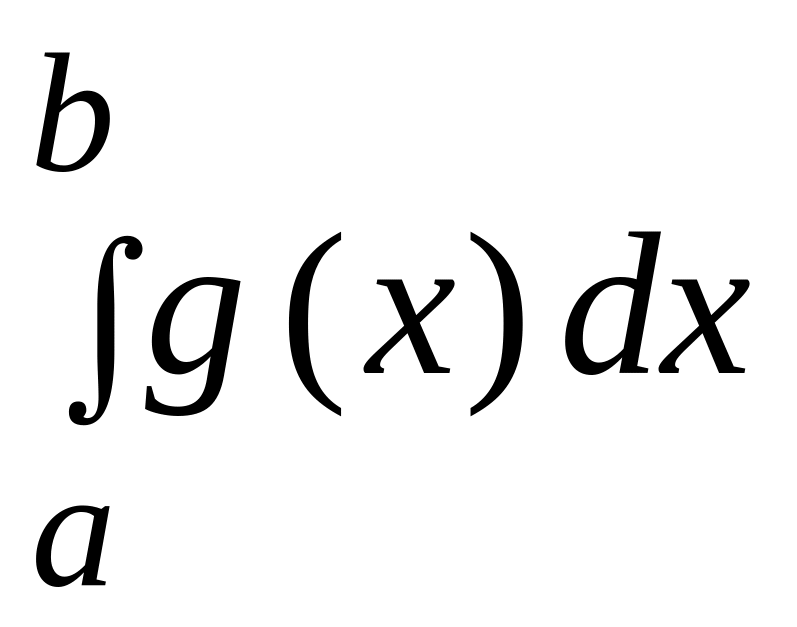следует
сходимость интеграла
,
а из расходимости интеграла
следует
расходимость интеграла
.
2.
Предельный
признак сравнения.
Пусть функции f
(x)
и g
(x)
непрерывны на промежутке [a;
b)
и в точке х
= b
терпят разрыв 2-го рода. Если существует
предел
= k,
0 < k
< ∞, то интегралы
и
сходятся
или расходятся одновременно.
3.
Если функция f
(x),
знакопеременная на промежутке [a;
b),
имеет разрыв 2-го рода в точке х
= b,
и несобственный интеграл
сходится, то сходится и интеграл
,
который в этом случае называется
абсолютно
сходящимся.
Замечание. В качестве эталона для сравнения функций часто берут функцию
g(x)
=
.
Несобственный интеграл
( p
> 0 ) сходится
при p
< 1 и
расходится при
p
≥ 1. Это
же относится и к интегралу
.
Пример 1.
Вычислить
несобственный интеграл
или установить его расходимость.
Подынтегральная
функция терпит разрыв при х = 3.
По определению:
=
=
=
arcsin
=
arcsin
– 0 =
.
Исходный интеграл сходится и равен
.
Пример 2. Вычислить
значение интеграла
.
Подынтегральная
функция терпит разрыв при х = 0.
По определению:
=
=
=
(x
lnx
–
x)
= –1 –
(ε
ln
ε
– ε)
= –1
–
0 = –1, т.к.
ε
ln
ε
=
=
=
= (– ε) = 0. Исходный интеграл сходится и равен –1.
Задание для самостоятельного решения
Найти значения несобственных интегралов или установить их расходимость:
Пример 3. Исследовать
на сходимость интеграл
.
Внутри отрезка
интегрирования [1;
1] функция
при х → 0 неограниченно возрастает.
По определению:
=
+
=
+
=
+
=
=
– 1
+
– 1
= ∞. Интеграл
расходится.
Задание для самостоятельного решения
Найти значения несобственных интегралов или установить их расходимость:
Пример 4.
Исследовать
на сходимость интеграл
.
Функция f
(x)=
терпит бесконечный разрыв в точке
х = 1. Перепишем ее в виде
f
(x)=
∙
и сравним ее с функцией g(x)
=
.
Согласно замечанию, интеграл
сходится
(р
= 2/3 < 1).
Т.к.
=
∙
∙
=
=
(≠ 0, ≠ ∞), то
в
соответствии с предельным признаком сравнения, исходный интеграл также сходится.
Задание для самостоятельного решения
Исследовать
сходимость несобственных интегралов:
Пример 5. Исследовать
на сходимость интеграл
.
Подынтегральная
функция f
(x)=
разрывна в точке х = 0.
Сравним ее с функцией
g(x)
=
.
Согласно замечанию, интеграл
сходится
(р
= 1/3 < 1). Т.к.
<
,
то по признаку сравнения исходный интеграл также сходится.
Задание для самостоятельного решения
Исследовать
сходимость несобственных интегралов:
