8. Определение линейных перемещений сечений балки и построение изогнутой оси

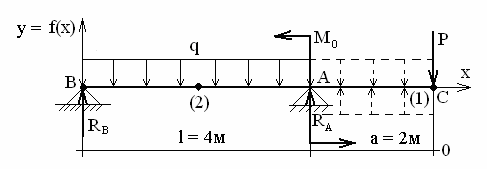
Для решения поставленной задачи найдем линейные перемещения (×)1 и (×)2 (рис. 1).

ПРИМЕЧАНИЕ: поместив начало координат в (×)С, мы вынуждены будем определять начальные параметры f₀ и V₀, т.е. f_C и V_C, которые не равны нулю.

Рациональнее повернуть балку на 180° (рис.5) так, чтобы левое крайнее сечение балки В находилось на опоре. При этом линейное (вертикальное) перемещение f_B = f₀ = 0.

Из условий закрепления балки, надо определить только V₀ = V_B :

Рис. 5

1. Разбиваем балку на два участка: ВА – I участок, АС – II участок

2. Записываем функцию М(x) поместив начало координат в (×) В.

M(x) = R_B x− ^qx2 _I +R_A(x−4)−M₀ (x−4)⁰ + ^q(x−4)2 _II

Записываем функцию углов поворота V(x), проинтегрировав (13):

(13)

выражение

V(x) =V + _EJz ^éR₂ 2 − ₆3

R_A(x−4)² M₀ (x−4) q(x−4)^{3 ù} I ^{2 1 6} II û

(14)

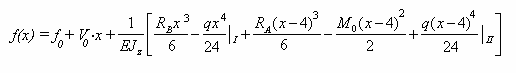
3

ë

. Записываем функцию линейных перемещений f(x), проинтегрировав выражение (14):

(15)

4. Записываем условия равенства нулю линейных перемещений на опорах В и А.

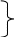1) f_(x=0)= f_В=0

(16) 2) f _(x=4м)= f_А =0

Из этих условий определяем начальные параметры f₀ и V₀. Используя первое условие, определяем: f₀=0.

Для определения V₀ используем второе условие. Сечение А принадлежит первому участку, поэтому записываем функцию f(x) для I участка и полагаем её равной нулю в сечение А, т.е. при значении координаты x = 4м.

f

4

x

1 qx

B

ê ú

0

ë û

×

ê ú

0

EJ 24

ë û

(x) =V x+ _EJz ^éR₆ 3 − ₂₄ ^ù (17) f (x = 4м) = 0 =V ×4+ ¹z ^éRB₆⁴3 − ^{q 4}4 ^ù (18)

1

= − − = − − =

V

ç ÷

ê ú

1

^éR_B ×4³ q×4^{4 ù} 1 ^æ17.5×10³ ×64 10×10³ ×256^{ö 0} 4EJ_{z ë} 6 24 _û 4×2×10 ¹ ×2760×10⁻⁸ _è 6 24 _ø

3

×

10 10 1

( )

8

=

1

−_{8×10 1 ×2760} 186,67−106,67 = − ₂₇₆

V

1

0

= − ₂₇₆ (19) 5. Вычисляем линейное перемещение (×) 1 (сечение С).

Сечение С принадлежит II участку, координата сечения x = 6м.

Записываем функцию f(x) с определенными выше значениями начальных параметров, подставляя координату х = 6м:

1

= − + × − + − + =

f

ç ÷

1

×6 1×10^{3 æ}17,5×6³ 10×6⁴ 42,5×2³ 30×2² 10×2^{4 ö (×)1(x=6м)} 276 2×10 ¹ ×2760×10⁻⁸ _è 6 24 6 2 24 _ø

=

5520

−0,022+ ^93,34 = −0,022+0,017 = −0,005м = −5мм

6. Вычисляем линейное перемещение (×) 2 (точка середины пролета АB). Точка 2 принадлежит I участку, ее координата х = 2м.

1

= − + × − =

f

ç ÷

1

×2 1×10^{3 æ}17,5×2³ 10×2^{4 ö (×)2(х=2м)} 276 2×10 ¹ ×2760×10⁻⁸ _è 6 24 _ø

=

1

−0,007+ ₅₅₂₀(23,33−6,67) = −0,007+0,003= −0,004м = −4мм

Знак (-) при вычислении V_0, f₁, f₂ указывает на то, что сечение В при изгибе поворачивается по часовой стрелке, сечения 1 и 2 перемещаются вниз от оси х.

7. Строим в масштабе изогнутую ось под эпюрой изгибающих моментов (рис.3в). Для построения изогнутой оси балки используем нулевые значения прогибов на опорах А и В и вычисленные прогибы сечений 1 и 2.

8. Удобно сопоставить очертание эпюры М(х) и изогнутой оси балки, ориентируясь на знак кривизны: на участке балки с отрицательным моментом – кривизна отрицательная; с положительным моментом – кривизна положительная.

Статически-неопределимые задачи плоского изгиба

Выше был рассмотрен пример решения статически-определимой балки (задачи № 6). Теперь рассмотрим пример решения статически-неопределимой балки (задача №7). Статически-неопределимыми балками называют такие балки, для определения неизвестных реакций опор в которых недостаточно только уравнений статического равновесия, т.к. число неизвестных реакций опор больше, чем число составленных уравнений статики. Для решения таких задач требуется составление дополнительных уравнений, связывающих неизвестные силы реакции опор. Такие уравнения, как правило, находятся из условий деформации балки, т.е. составляются на основе уравнений перемещений.

ЗАДАЧА №7

Для балки, изображенной на рис. 1, требуется построить эпюры Q(x), M(x) в долях ql²; эпюру прогибов f(x), вычислив прогибы сечений (1) и (2).

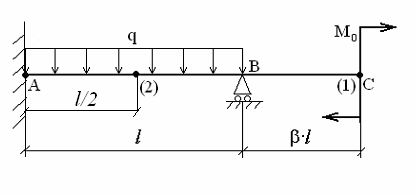Рис.1 – Заданная схема

Д

2

ано: q; l; b = 0.5, М₀ = ^ql2 , ЕJ_z

РЕШЕНИЕ

1) Составляем план сил (рис.2). Для этого мысленно убираем опоры (сечение А и сечение В) и заменяем их связями (Н_А; R_A; M_A и R_B).

2

å

) Составим уравнения статического равновесия: 1. x = 0;H_A = 0

2

å

B

å

A

2

. y = 0;R_A −ql + R = 0 (1) 3. M( ) = 0;M_A − ^ql2 + R_Bl −M₀ = 0

Трех уравнений равновесия недостаточно для однозначного определения четырёх неизвестных сил реакций опор (подчеркнуты).

В нашей задачи имеем четыре неизвестные реактивные силы, и систему из трёх уравнений статики.

−

1 x

A B

ê

0

6 6

ú

Разность между числом неизвестных, входящих в уравнения статики, и числом составленных уравнений статики называется степенью статической неопределимости. Степень статической неопределимости показывает, сколько дополнительных уравнений необходимо составить к уравнениям статики. Эта задача статически-неопределимая один раз. Таким образом, необходимо составить одно дополнительное уравнение, связывающее неизвестные силы реакции.

3) Воспользуемся методом начальных параметров и запишем функцию, описывающую линейные перемещения сечений балки (рис.2). Начало координат помещаем в левое крайнее сечение А. Разбиваем балку на участки – их два: АВ и BС.

f (x) = f₀ +V x+ _EJz ^éRAx3 − ^M₂^x2 − _I + ^{R (x−l)}3 + ^q( ₂₄^l)4

ù

II û

(2)

Д

ë

ля нахождения начальных параметров f₀ и V₀, входящих в выражение (2), записываем условия равенства нулю перемещений на опорах А и В.

1) f_(x=0)= 0 Þ f₀ = 0 2) V_(x=0)= 0 Þ V₀ = 0

3) f_(x=l)= 0 (на опоре В f=0) Используя эти условия, получаем следующее уравнение:

f

æ ö

4

ql

1

6 2

è ø

4

_(x=l) = 0 = _EJz _ç ^RAl3 − ^MAl2 −_{24 ÷} (3) Т.к. EJ_z ¹ 0, получаем,

^R

ql

6 2

^Al3 − ^MAl2 −−₂₄ = 0 (4)

Уравнение (4) является четвёртым уравнениям, дополняющим систему уравнений (1).

4

å

) Решаем следующую систему, состоящую из четырёх уравнений, в состав которых входят четыре неизвестных реактивных силы.

1. x = 0;H_A = 0

2

å

B

. y = 0;R_A −ql + R = 0

3

å

)

2

. M(A = 0;M_A − ^ql2 + R_Bl −M₀ = 0 (5)

4

4

ql

6 2

.^RAl3 − ^MAl2 −−₂₄ = 0

Решаем систему уравнений (5). Домножим обе части уравнения 2. на (- l) и сложим с уравнением 3.

−R_Al +ql² − R_Bl = 0

M

B

2

_A − ^ql2 + R l −M₀ = 0

+ +

+ −

M M

−

2

R_Al +ql² + M_A − ^ql2 −M₀ = 0 (6)

R

M

M M

2 2

_A = ql + _l^A −^ql − _l⁰ == ^ql + _l^A − _l⁰ ₍₇₎ Подставляем значение R_A из (7) в уравнение 4. системы (5):

₁

4 4

M

M M

ql ql

0

A A

2 + ₆^l2 − ₆^l2 − ₂^l2 − ₂₄= 0 (8) Из (8) определяем М_А, приведя к общему знаменателю

2ql⁴ +4M_Al² −4M₀l² −12M_Al² −ql⁴ = 0 (9) ql⁴ −8M_Al² −2ql⁴ = 0 (10)

M

8

_A = − ^ql2 (11)

Определяем реакцию R_B из уравнения 3. системы (5):

ql² ql² ql² ql²

⁰

= =

R

2 ^A 2 2 8 ^B l l

= ⁹ ql ₍₁₂₎

О

8

пределяем реакцию R_А из уравнения 2. системы (5):

R

8 8

_A = ql − ⁹ ql = − ^ql ₍₁₃₎

Определение всех неизвестных сил реакции опор означает раскрытие статической неопределимости.

5) В качестве проверки составляем уравнение моментов относительно (×) В: å^{M(B) = 0}

M

2

_A − R_Al + ^ql2 −M₀ = 0 (14)

−

8 8 2 2

^ql2 + ^ql2 + ^ql2 − ^ql2 = 0

Реакции найдены верно.

6) Построение эпюр Q(x) и M(x).

Рассмотрим I участок (АВ).

Пометим начало координат этого участка в (×) А. Произвольно выбранное сечение на этом участке может принимать следующие значения:

0

1

£ x £ l

Внутренняя поперечная сила на участке АВ:

Q

1 1 1

8

(x ) = R_A −qx = − ^ql −qx (15)

Внутренний изгибающий момент на участке АВ

M

ql

1 1 1

1 1

2 8 2

(x ) = −M_A + R_Ax − ^qx2 = ₈2 − ^qlx − ^qx2 (16)

Рассмотрим II участок (CB).

Поместим начало координат участка СВ– в (×) С. Произвольно выбранное сечение на этом участке принимает следующие значения:

0 £ x₂ £ 0,5l

Внутренняя поперечная сила на участке СВ:

Q(x₂ ) = 0 (17) Внутренний изгибающий момент на участке АВ

M

2 8

(x₂ ) = −M₀ = const = − ^ql2 = − ⁴ ql² (18)

Функции Q(x) и M(x) для этих участков строим графически в масштабе в долях ql под схемой балки (рис.2а,б).

7) Построение изогнутой оси балки.

Для графического изображения изогнутой оси балки необходимо вычислить значения линейных перемещений нескольких сечений (точнее -центров тяжести этих сечений) балки. В рассматриваемой задаче (рис.2) вычисляем вертикальные перемещения сечений (×)1 и (×)2 – середина пролета l. Вертикальные перемещения сечений А и В известны – f_A f_B = 0, так как эти сечения расположены на опорах.

Воспользуемся написанной функцией (2) линейных перемещений сечений балки. В функцию (2) подставим координату сечения (×)1 (x =1,5l). Это сечение принадлежит II участку, поэтому в выражении (2) учитываем все слагаемые до скобки с цифрой II:

₁

= − − + + =

f

ê ú

=

é_RA(1,5l)³ _MA(1,5l)² _q(1,5l)⁴ _{RB (1,5l −l)}³ _{q(1,5l −l)}⁴ ù (×)C(x 1,5l) ^EJz ë ^{6 2 24 6 24} û

4

é ù

1 9

ql ql ql ql ql

4 4 4 4

=

ë û

_EJz _ê− ₄₈ (1,5)³ + ₁₆ ×(1,5)² − ₂₄ ×(1,5)⁴ + ₄₈ (0,5)³ + ₂₄ (0,5)⁴ _ú =

^q

= − + − + +

= −

0,114

ç ÷

^l4 æ ^{3,375 2,25 5,06 1,125 0,0625}ö ^ql4

^EJ_z è ^{48 16 24 48 24} ø ^EJ_z

Линейное перемещение (×)2 вычисляем, подставив в функцию (2) координату этого сечения (x = 0,5l). В выражении (2) учитываем слагаемые до скобки с цифрой I, т.к. это сечение принадлежит I участку.

₁

= − − =

f

ê ú

é_RA(0,5l)³ _MA(0,5l)² _q(0,5l)⁴ ù (×)2(x=0,5l) ^EJz ë ^{6 2 24} û

4

é ù

ql ql ql

1

4 4

=

ê ú

_EJz ë− ₄₈ ×0,125+ ₁₆ ×0,25− ₂₄ ×0,0625û =

⁼

EJ EJ

^ql4 (^{0,0026+0,016−0,0026})^{= 0,01 ql}4 z z

Перемещение сечения (×)1 в расчете получилось со знаком минус, это указывает на то, что сечение (×)1 сместилось вниз. Соответственно сечение (×)2 сместилось вверх.

По полученным значениям перемещений сечений (×)1 и (×)2, а также с учетом равенства нулю перемещений сечений А и В, строим в масштабе изогнутую ось балки под эпюрой M(x) (рис.2в).

Удобно сопоставить очертание эпюры M(x) (рис.2б) с изображением изогнутой оси балки (рис.2в): положительные значения моментов эпюры M(x) указывают на то, что кривизна изогнутой оси балки на этом интервале положительная; отрицательные значения моментов эпюры M(x) соответствуют отрицательной кривизне изогнутой оси балки.

Из полученных результатов можно сделать выводы:

1. Опасными сечениями балки являются все сечения, принадлежащие участку ВС, т.к. на этом участке наблюдается наибольшее по абсолютной

в

4

еличине значение внутреннего изгибающего момента M_max = ₈ ql² .

2

EJ

. Наибольшее линейное перемещение (прогиб) испытывает сечение балки (×)1, f_max = 0,11 ^ql4 .

z

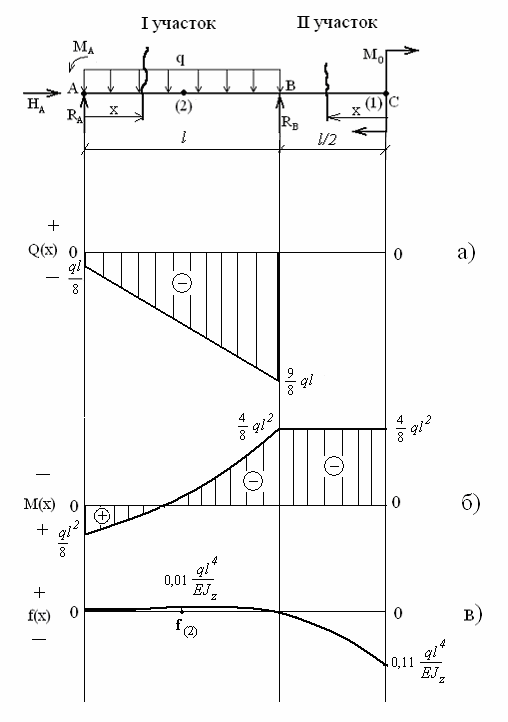Рис. 2

ЛИТЕРАТУРА

1. Методические указания по сопротивлению материалов для студентов заочной формы обучения: метод указания / сост.: Е. С. Цобкалло, Л. Н. Петрова, Е. А. Разумовская. – СПб.: СПГУТД, 2007. – 25 с.

2. 1. Феодосьев, В. И. Сопротивление материалов: учебник для вузов. – 10-е изд., перераб. и доп. / В. И. Феодосьев.– М. : Изд-во МГТУ им. Н. Э. Баумана, 2000. – 591 с.

3. Беляев, Н. М. Сборник задач по сопротивлению материалов: учеб. пособие для вузов / Н. М. Беляев. – СПб.: Иван Федоров, 2003. – 432 с.

4. Беляев, Н. М. Сопротивление материалов / Н.М. Беляев. – М.: Наука, 1976. – 608 с.

5. Дарков, А В. Сопротивление материалов / А. В. Дарков, Г. С. Шпиро – М.: Высшая школа, 1969. – 656 с.

6. Межецкий Г. Д. Сопротивление материалов / Г. Д. Межецкий и др.: учебник. - М.: «Дашков и К°», 2008. – 415 с.

7. Ицкович, Г. М. Сопротивление материалов / Г. М. Ицкович: учебник для машиностроительных техникумов. – 9-е изд., стер. - М.: Высшая школа, 2001. - 368 с.

Содержание ВВЕДЕНИЕ..................................................................................................................................2

1.1. Классификация внешних нагрузок .................................................................................3 1.2. Способы закрепления элементов конструкции .............................................................4 1.3. Способ приложения нагрузок..........................................................................................5 2. План рассмотрения нагружено-деформированных состояний...........................................8 2.1. Понятие силового участка ...............................................................................................8 2.2. Правило определения внутренних силовых факторов (метод сечений).....................8 3. Осевое растяжение (сжатие)...................................................................................................9 3.1. Определение внутреннего продольного усилия..........................................................10 3.2. Построение эпюры внутреннего продольного усилия................................................11 3.3. Проверка прочности, подбор сечения элемента..........................................................12 ЗАДАЧА №1 ..............................................................................................................................13 ЗАДАЧА №2 ..............................................................................................................................16 4.Линейное, плоское и объёмное напряжённые состояния...................................................21 4.1. Линейное напряженное состояние................................................................................21 4.2. Плоско-напряженное состояние....................................................................................23

4.3. Графический способ решения прямой и обратной задач плоско-напряженного состояния (круг Мора)...........................................................................................................26

4.3.1. Прямая задача плоско-напряженного состояния (определение напряжений на наклонных площадках)......................................................................................................26 4.3.2. Обратная задача напряженного состояния (определение напряжений на главных площадках) ..........................................................................................................27

4.4. Объемно-напряженное состояние.................................................................................28 ЗАДАЧА №3 ..............................................................................................................................30 5. Сдвиг.......................................................................................................................................34 5.1. Касательные напряжения при чистом сдвиге..............................................................34 5.2 Деформации при сдвиге..................................................................................................36 6. Кручение.................................................................................................................................37 6.1 Внешние и внутренние силовые факторы, метод сечений..........................................37 6.2 Напряжения и условие прочности при кручении.........................................................40 6.3 Деформации и условие жесткости при кручении.........................................................42 ЗАДАЧА №4 ..............................................................................................................................44 7. Геометрические характеристики плоских сечений............................................................48 ЗАДАЧА №5 ..............................................................................................................................52 8. Плоский поперечный изгиб..................................................................................................57 8.1 Внешние и внутренние силовые факторы, метод сечений..........................................57 8.1.1. Активные внешние силовые факторы ...................................................................57 8.1.2. Реактивные внешние силовые факторы ................................................................57

8.1.3. Внутренние силовые факторы. Дифференциальные зависимости между Q(x) и M(x). ....................................................................................................................................58

8.2 Нормальные и касательные напряжения при изгибе. Условие прочности................60 8.3 Главные напряжения при плоском поперечном изгибе...............................................61 8.4 Деформации и условие жесткости при плоском поперечном изгибе........................62 ЗАДАЧА №6 ..............................................................................................................................67 8.5 Статически-неопределимые задачи плоского изгиба ..................................................80 ЗАДАЧА №7 ..............................................................................................................................80 ЛИТЕРАТУРА ...........................................................................................................................86