Вопрос 5 Уравнение неразрывности (сплошности) потока.

Рассмотрим поток жидкости, в котором нет пустот и трещин, без внутренних источников субстанции (γ = 0). Перенос осуществляется только конвективным механизмом (q_м = 0), т.е.  Тогда основное уравнение переноса субстанции имеет следующий вид: Расписав дивергенцию векторной функции   как скалярную величину и подставив ее в уравнение (1.27), получим уравнение неразрывности и сплошности потока:

(1.28)

Уравнение неразрывности потока может быть записано в виде:

Частные случаи уравнения неразрывности потока: а) процесс стационарный ( ):

или  ;

(1.30)

б) жидкость несжимаема (ρ = const):  или в) однонаправленное движение вдоль оси Х ( ): г) однонаправленное движение и процесс стационарный ( ; ):

или  .

(1.33)

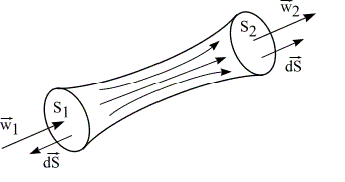Рисунок 1.3 – К уравнению неразрывности и сплошности потока

Вопрос 6 Распределение скоростей и расход жидкости при установившемся ламинарном потоке.

Основной задачей гидравлического расчета движения жидкостей через трубы является определение скоростей движения и расхода жидкости.

Решим задачу по определению скоростей движения и расхода жидкости сначала для ламинарного режима движения, т.е. строго упорядоченного, слоистого течения жидкости, а затем для турбулентного режима.

Рассмотрим установившееся движение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром d = 2r_o, расположенной горизонтально. Рассмотрим это движение достаточно далеко от входа жидкости в трубу, где поток уже полностью сформировался(рис. 10.2).

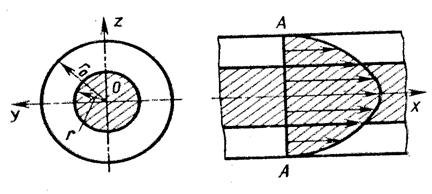Рис. 10.2. Эпюра скоростей при ламинарном движении жидкости

При ламинарном движении наибольшая скорость развивается в центре трубы, наименьшая -у стенок. Закон распределения скоростей в поперечном сечении потока при ламинарном режиме можно установить следующим образом.

Выделим внутри трубы цилиндр сечениями 1–1 и 2–2, цилиндр диаметром 2r и длиной l. Пусть давления жидкости в сечениях равны p₁ и p_2. Тогда на выделенный цилиндр жидкости действуют силы: P₁, P₂ – силы давления на торцы цилиндра; T – сила трения, действующая по боковой поверхности цилиндра (рис.10.3).

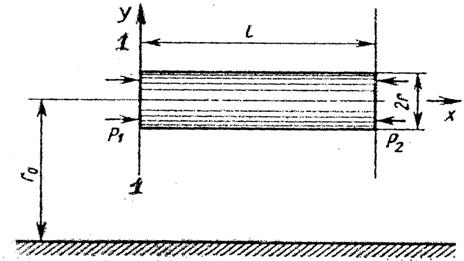Рис. 10.3. К выводу закона распределения скоростей

при ламинарном режиме

Так как цилиндр вместе с основной массой жидкости движется прямолинейно и равномерно, то действующие на него силы находятся в равновесии. Запишем уравнение проекций сил на ось движения P₁- P₂- T= 0, (10.1)

где  P₁ = p₁pr²;  P₂ = p₂pr²;  T = - m2prldv/dr. В этих выражениях r– радиус и v – скорость движения выделенного цилиндра -это переменные величины; m– динамический коэффициент вязкости жидкости.

После подстановки значений переменных в уравнение (10.1) и некоторых преобразований получим

dv= - prdr/2ml, где p = p₁ - p₂.

После интегрирования полученного выражения по r в пределах от 0 до r_o получаем v= p(r_o²- r²)/4ml. (10.2)

Выражение является законом распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени.

Максимальная скорость жидкости имеет место в центре сечения трубы (при r = 0) v_max= pr_o²/4ml.  (10.3)

Определим теперь объемный расход жидкостипри ламинарном течении. Выделим кольцевой слой жидкости толщиной dr, который находится на расстоянии r от оси трубы. Все частицы жидкости этого слоя имеют скорость v, определяемую формулой (10.2). Площадь рассматриваемого кольцевого слоя равна dF= 2prdr.

Элементарный расход жидкости при этом равен произведению скорости v на элементарную площадь кольцевого слоя dF, т.е. dQ= vdF. Интегрируя это выражение в пределах от r = 0 до r = r_o, получим искомое выражение (формулу Пуазейля) Q= ppr_o⁴/8ml. (10.4)

Применим полученный закон распределения скоростей и расхода жидкости для определения средней скорости потока жидкости в рассматриваемом трубопроводе.

Из уравнения неразрывности потока жидкости в трубопроводе  Q= v₁F₁= v₂F₂= ... = v_срF = const

определяем среднюю скорость v_ср= Q/F= pr_o²/8ml. (10.5)

Из сравнения максимальной скорости (формула (10.3)) и средней скорости (формула (10.5)) следует, что средняя скорость при ламинарном течении в 2 раза меньше максимальной скорости, т.е.v_ср= 0.5v_max. (10.6)