Вопрос 1 Основные физико-химические величины: плотность, удельный вес, вязкость, поверхностное (межфазное) натяжение.

Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму илиплощади (поверхностная плотность). Более строгое определение плотности требует уточнение формулировки:

Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется простоплотностью тела.

Плотность вещества — это плотность тел, состоящих из этого вещества. Отсюда вытекает и короткая формулировка определения плотности вещества: плотность вещества — это масса его единичного объёма.

Плотность тела в точке — это предел отношения массы малой части тела ( ), содержащей эту точку, к объёму этой малой части ( ), когда этот объём стремится к нулю^[1], или, записывая кратко,  . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.

Виды плотности и единицы измерения

Исходя из определения плотности, её размерность кг/м³ в системе СИ и в г/см³ в системе СГС.

Для сыпучих и пористых тел различают:

истинную плотность, определяемую без учёта пустот;

удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.

Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.

Формула нахождения плотности

Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:

где m — масса тела, V — его объём; формула является просто математической записью определения термина «плотность», данного выше.

При вычисления плотности газов эта формула может быть записана и в виде:

где М — молярная масса газа,   — молярный объём (при нормальных условиях равен 22,4 л/моль).

Плотность тела в точке записывается как   тогда масса неоднородного тела (тела с плотностью, зависящей от места) рассчитывается как 

Зависимость плотности от температуры

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза ичугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого числа.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Правда, вода является исключением из этого правила, её плотность при затвердевании уменьшается.

Наряду с понятием плотности, часто пользуются понятием удельного веса вещества. Удельным весом данного вещества называют отношение веса Р однородного тела из данного вещества к объему тела. Обозначим удельный вес буквой γ. Тогда

Можно также сказать, что удельный вес есть сила тяжести единицы объема данного вещества.

Удельный вес и плотность относятся друг к другу так же, как вес и масса тела:

За единицу удельного веса принимается: в системе СИ — 1 н/м³, в системе СГС —1 дин/см³, в системе МКСС— 1 кГ/м³. Эти единицы связаны между собой соотношениями

1 н/м³ = 0,1 дин/см³ = 0,102 кГ/м³.

Часто пользуются внесистемной единицей 1 Г/см³.

Так как масса вещества, выраженная в г, равна его весу, выраженному в Г, то удельный вес вещества, выраженный в этих единицах, численно равен плотности этого вещества, выраженной в системе СГС. Подобное же численное равенство имеется и между плотностью в системе СИ и удельным весом в системе МКСС.

Вязкость При движении реальной жидкости в ней возникают силы внутреннего трения между молекулами и слоями жидкости, оказывающие сопротивление движению. Свойство жидкости оказывать сопротивление движению называется вязкостью. Слой жидкости можно представить как слой, состоящий из бесконечно большого числа элементарных слоёв, расстояние между которыми бесконечно мало и составляет   (рис. 1.1). Если учесть, что вязкость – это результат касательного напряжения (трения) между соприкасающимися слоями жидкости, то скорость их движения будет различна. Верхний слой будет двигаться со скоростью несколько большей, чем нижний, на бесконечно малую величину  . 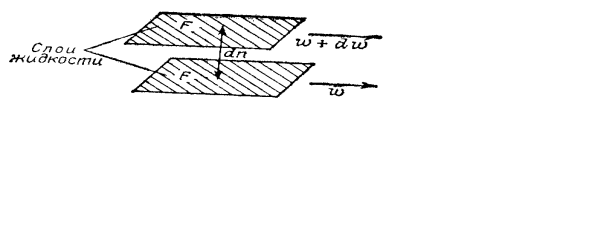Рис.1.1. К пояснению закона Ньютона. На границе с соседним слоем возникает сила трения  , направленная в сторону, противоположную движению слоёв жидкости. Эта сила трения пропорциональна площади соприкосновения слоёв F и градиенту скорости  , характеризующему изменение скорости, приходящееся на единицу расстояния между слоями по нормали Коэффициент пропорциональности   называется динамической вязкостью. Отношение   обозначают через   и называют напряжением внутреннего трения (напряжением сдвига): Знак минус указывает на то, что касательное напряжение (напряжение сдвига) тормозит слой жидкости, движущейся с относительно большей скоростью. Из уравнения (1.8) вытекает размерность вязкости в системе СИ  . Уравнение (1.8) выражает закон внутреннего трения Ньютона, согласно которому напряжение внутреннего трения, возникающее между слоями жидкости при её движении, прямо пропорционально градиенту скорости. Жидкости, подчиняющиеся этому закону, называются ньютоновскими. Они имеют низкую молекулярную массу (вода, воздух, спирты, газы и др.). Жидкости, которые не подчиняются закону, называются неньютоновскими. Они имеют большую молекулярную массу (пасты, гели, растворы полимеров).  Динамический коэффициент вязкости для газов при температурах отличных от   рассчитывают по формуле: где   - динамический коэффициент вязкости при  ; Т - температура, К; С - постоянная Сатерленда, зависящая от свойств газа [1]. Для газовых смесей динамический коэффициент вязкости находят из выражения: где   - значения динамических коэффициентов вязкости смеси и ее отдельных компонентов;  - объемные (мольные) доли компонентов смеси;   - мольная масса смеси;   - мольные массы компонентов смеси. Динамический коэффициент вязкости жидких смесей: 

где   - мольные доли компонентов смеси. Для разбавленных суспензий динамический коэффициент вязкости определяют в зависимости от содержания твердой фазы  (по объему):

а) при    б) при    ;

(1.12) (1.13)

где  - коэффициент динамической вязкости жидкости;   - объемная доля твердой фазы в суспензии. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ, стремление в-ва (жидкости или твердой фазы) уменьшить избыток своей потенциальной энергии на границе раздела с др. фазой (поверхностную энергию). Определяется как работа, затрачиваемая на создание единицы площади пов-сти раздела фаз (размерность Дж/м²). Согласно др. определению, поверхностное натяжение-сила, отнесенная к единице длины контура, ограничивающего пов-сть раздела фаз (размерность Н/м); эта сила действует тангенциально к пов-сти и препятствует ее самопроизвольному увеличению.

Поверхностное натяжение-осн. термодинамич. характеристика поверхностного слоя жидкости на границе с газовой фазой или др. жидкостью. Поверхностное натяжение разл. жидкостей на границе с собств. паром изменяется в широких пределах: от единиц для сжиженных низкокипящих газов до неск. тыс. мН/м для расплавл. тугоплавких в-в. Поверхностное натяжение зависит от т-ры. Для мн. однокомпо-нентных неассоциир. жидкостей (вода, расплавы солей, жидкие металлы) вдали от критич. т-ры хорошо выполняется линейная зависимость:

где  и s₀-поверхностное натяжение при т-рах T и T₀ соотв.,  0,1 мН/(м·К)-температурный коэффициент поверхностного натяжения. Осн. способ регулирования поверхностного натяжения заключается в использовании поверхностно-активных веществ (ПАВ).

Поверхностное натяжение входит во мн. ур-ния физики, физ. и коллоидной химии, электрохимии. Оно определяет след. величины: 1) капиллярное давление   , где r₁ и r₂ -главные радиусы кривизны пов-сти, и давление насыщ.пара р_r над искривленной пов-стью жидкости:  , где r-радиус кривизны пов-сти, R -газовая постоянная, V_n-молярный объем жидкости, p₀- давление над плоской пов-стью (законы Лапласа и Кельвина, см. Капиллярные явления).

2) Краевой угол смачивания   в контакте жидкости с пов-стью твердого тела: cos  , где  -уд. своб.поверхностные энергии твердого тела на границе с газом и жидкостью,  -поверхностное натяжение жидкости (закон Юнга, см. Смачивание).

3) Адсорбцию ПАВ   где -хим. потенциал адсорбируемого в-ва (ур-ние Гиббса, см. Адсорбция). Для разб. р-ров  где с-молярная концентрация ПАВ.

4) Состояние адсорбц. слоя ПАВ на пов-сти жидкости: (_s + a/A²)·(A - b)= kT, где _s = (₀ — ) - двухмерное давление, ₀ и <т-соответственно поверхностное натяжение чистой жидкости и той же жидкости при наличии адсорбц. слоя, а -постоянная (аналог постоянной Ван-дер-Ваальса), A-площадь поверхностного слоя, приходящаяся на одну адсорбир. молекулу, b -площадь, занимаемая 1 молекулой жидкости, k -постоянная Больцмана (ур-ние Фрумкина-Фольмера, см. Поверхностная активность).

5)Электрокапиллярный эффект: — d/d = r_s, где r_s-плотность поверхностного заряда, -потенциал электрода (ур-ние Липмана, см. Электрокапиллярные явления).

6) Работу образования критич. зародыша новой фазы W_c. Напр., при гомог. конденсации пара при давлении   , где p₀- давление пара над плоской поверхностью жидкости (ур-ние Гиббса, см. Зарождение новой фазы).

7) Длину  капиллярных волн на пов-сти жидкости:   , где -плотность жидкости, т-период колебаний, g-ускорение своб. падения.

8) Упругость жидких пленок со слоем ПАВ: модуль упругости   , где s- площадь пленки (ур-ние Гиббса, см.Тонкие пленки).

Поверхностное натяжение измерено для мн. чистых в-в и смесей (р-ров, расплавов) в широком интервале т-р и составов. Поскольку поверхностное натяжение весьма чувствительно к наличию примесей, измерения разными методиками не всегда дают совпадающие значения. Осн. методы измерения следующие:

1) подъем смачивающих жидкостей в капиллярах. Высота подъема   , где   -разность плотностей жидкости и вытесняемого газа, r-радиус капилляра. Точность определения поверхностного натяжения растет с уменьшением отношения r/а (а-капиллярная постоянная жидкости).

2) Измерение макс. давления в газовом пузырьке (метод Ребиндера); расчет основан на ур-нии Лапласа. При выдавливании пузырька в жидкость через калиброванный капилляр радиусом г перед моментом отрыва давление

3) Метод взвешивания капель (сталагмометрия):   (ур-ние Тейта), где G-общий вес n капель, оторвавшихся под действием силы тяжести от среза капиллярной трубки радиусом r. Для повышения точности правую часть умножают на поправочный коэф., зависящий от г и объема капли.

4) Метод уравновешивания пластины (метод Вильгельми). При погружении пластины с периметром сечения L в смачивающуюжидкость вес пластины   , где G₀- вес сухой пластины.

5) Метод отрыва кольца (метод Дю Нуи). Для отрыва проволочного кольца радиусом R от пов-сти жидкости требуется сила 

6) Метод сидящей капли. Профиль капли на несмачиваемой подложке определяется из условия постоянства суммы гидростатич. и капиллярного давлений. Дифференциальное ур-ние профиля капли решается численным интегрированием (метод Башфорта-Адамса). По измерениям геом. параметров профиля капли с помощью соответствующих таблиц находят поверхностное натяжение.

8) Метод вращающейся капли. Капля жидкости плотностью r₁ помещается в трубку с более тяжелой (плотность r₂) жидкостью. При вращении трубки с угловой скоростью  капля вытягивается вдоль оси, принимая приближенно форму цилиндра радиуса r. Расчетное ур-ние:   . Метод применяют для измерения малых поверхностных натяжений на границе двух жидкостей.

Поверхностное натяжение является определяющим фактором мн. технол. процессов: флотации, пропитки пористых материалов, нанесе-ния покрытий, моющего действия, порошковой металлургии, пайки и др. Велика роль поверхностного натяжения в процессах, происходящих в невесомости.

Понятие поверхностного натяжения впервые ввел Я. Сегнер (1752). В 1-й пол. 19 в. на основе представления о поверхностном натяжении была развита мат. теория капиллярных явлений (П. Лаплас, С. Пуассон, К. Гаусс, А.Ю. Давидов). Во 2-й пол. 19 в. Дж. Гиббс развил термодинамич. теорию поверхностных явлений, в к-рой решающую роль играет поверхностное натяжение. В 20 в. разрабатываются методы регулирования поверхностного натяжения с помощью ПАВ и электрокапиллярных эффектов (И. Ленгмюр, П. А. Ребиндер, A. H. Фрумкнн). Среди совр. актуальных проблем-развитие мол. теории поверхностного натяжения разл. жидкостей (включая расплавл. металлы), влияние кривизны пов-сти на поверхностное натяжение.