§11.4 Внутренняя энергия идеального газа.

Внутренняя энергия идеального газа состоит из учета потенциальной энергии и кинетической энергии движения атомов или молекул, поэтому величина внутренней энергии определяются выражением:

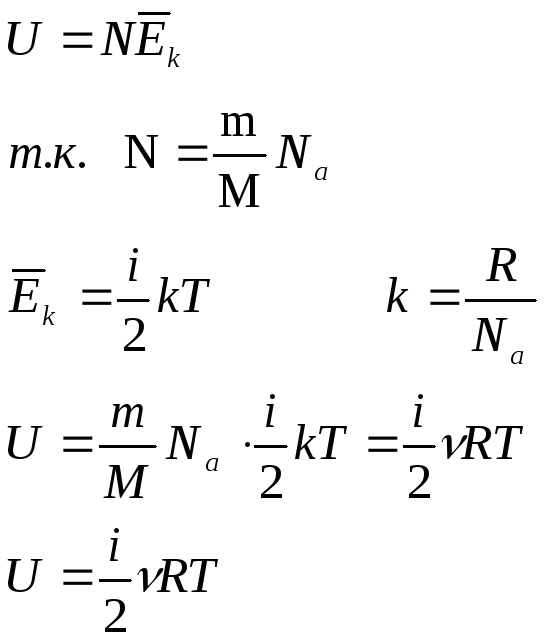
Внутренняя энергия – это функция состояние газа. Она прямо пропорциональна абсолютной температуре и характеризует энергию всех молекул газа.

Глава 12. Статистические распределения

§12.1 Распределения Максвелла молекул по скоростям.

Введенная ранее средняя квадратичная скорость характеризует среднюю интенсивность движения, ясно, что при хаотическом движении молекулы движутся с различными скоростями. Очевидно, что число молекул с очень маленькими скоростями, как и число молекул со скоростями сравнительно невелико. Основное количество молекул имеет скорости близкие к _КВРаспределение по скоростям установил Максвелл. Для этого он ввел функцию распределенияf_(). Физический смысл этой функции заключается в том, что она позволяет вычислить число молекулdNдвижущихся со скоростями в интервале (,+d)dN=f_()d

В конечном интервале (1,2):

Графическая зависимость функции распределения от скорости имеет вид:

Аналитический вид:

(N–общее число молекул) (m₀– масса одной молекулы)

-наиболее вероятная скорость

- средняя арифметическая скорость

- средняя квадратичная скорость.

При увеличении температуры интенсивность движения возрастает

§12.3 Барометрическая формула.

Распределение молекул в поле силы тяжести является неравномерным. В жидкостях давление на различных глубинах различно в следствии гидростатического давления.

Для газов это соотношение может быть записано только для малых толщин:

т.о.

т.о.

- барометрическая формула. Вывод получен при условии, что температура на всех высотах одинакова.

§12.4 Распределение Больцмана.

Распределение Больцмана – распределение частиц в потенциальном поле. Барометрическая формула является частным случаем распределения частиц в потенциальном поле. Преобразуем его используя уравнение Менделеева-Клапейрона в виде: p=nkT

-распределение Больцмана.

Анализ:

1)T∞, следовательноW_П/kT0,n=n₀

2)T0, след.W_П/kT∞,n0, Все молекулы падают на землю.

Глава 13. Физическая кинетика

13.1 Длина свободного пробега.

Длина свободного пробега – расстояние между двумя последовательными соударениями молекул в газе.<λ> Достаточно большой круг явлений может быть описан с помощью простейшей механической модели, согласно которой молекулы представлены в виде шариков, которые испытывают упругие соударения между собой и стенками сосуда. Минимальное расстояние, на которое могут сблизиться молекулы называется эффективным диаметром и принимается за диаметр шариков.

Круг площадьюd²- называется эффективным сечением. Найдем среднее число соударений которые испытывает молекулы при хаотическом движении <Z>; Пусть все молекулы покоятся и движется только одна. За 1 сек. молекула пройдет расстояние равное <>

При этом она столкнется со всеми молекулами которые находятся в пределах эффективного сечения т.е. находится в цилиндре высотой <> и площадью сечения равнойd²еслиn– концентрация молекул, то <Z>=nV=nd²<>

Учет движения всех частиц приведет к:

Средний путь за 1 сек. т.е. длина свободного пробега: