Глава 4. Закон всемирного тяготения

§4.1 Закон всемирного тяготения.

Сила, с которой две материальные точки притягивают друг друга, пропорциональна массам этих точек и обратно пропорциональна квадрату радиуса между ними:

Для тел с разной формой:

, где=6.67*10^-11Нм²/кг²

– напряженность гравитационного поля.

гдеe_r - орт радиус-вектора из материальной точки в данную точку поля.

– потенциальная энергия точкиm`

- потенциал гравитационного поля.

A₁₂=U₁-U₂=m`(<sub>1</sub>-<sub>2</sub>); => m` F=m`G, U=m`

Космические скорости:

=>1-я космическая = 8км/с

A`=Uнач-Uкон,

Uкон=0;;;,

A=mgR- работа для преодоления сил гравитации

=>V₂=2-я космическая = 11км/с

Глава 5. Динамика вращательного движения

§5.1 Кинематические характеристики вращательного движения.

Если точка движется криволинейно, то в каждый момент времени ее движение может быть представлено как движение по окружности с радиусомR. Ее движение может быть описано с помощью радиус-вектора, который проведен из (0;0) в точку, где находится тело:

R=rsin, V=rsin,

§5.2 Момент силы. 2-й закон Ньютона для вращательного движения.

Опыт показывает, что одна и та же сила оказывает разное вращательное действие.

M=FRsinα

F_τ=Fsinα

M=F_τR

Д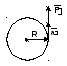ействие касательной силы на материальную точку может привести к движению с тангенсальным ускорением:

F_=ma_

a=R

F_= mR

F_R=mR²

M=J

M=F_ R

J=mR²- момент инерции

– угловое ускорение

§5.3 Момент импульса точки.

2-й закон Ньютона для вращательного движения (в другой форме).

- Момент импульса

- в импульсной форме

Действие момента силы равно скорости изменения момента импульса

(Если M –const)

(при М -const)

L=J=mR²=mR²/R=mR момент импульса и импульс точки связаны между собой

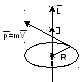
Момент импульса можно определить и относительно начала координат

L=mrsin

§5.4 Динамика вращательного движения твёрдого тела.

Абсолютно твёрдым телом называют совокупность материальных точек, жестко связанных между собой.

2-й з-н Ньютона вращательного движения для каждой точки

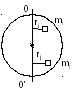
- результирующий момент всех сил.

- момент инерции твёрдого тела.

Момент инерции характеризует меру инертности тела при вращательном движении. Его величина зависит от массы тела, а также от распределения массы относительно оси вращения каждое тело может иметь бесчисленное количество моментов инерции определяемых относительно разных осей вращения.

Таким образом, получили основной закон динамики вращательного движения:

§5.5 Закон сохранения момента импульса.

Из основного закона динамики вращательного движения следует: если результирующий момент сил равен нулю, соответственно dL/dt=0, то означает суммарный момент импульса остаётся постоянным. Таким образом, если на систему не действуют ни ускорение, ни тормозящие моменты сил, то величина и направление момента импульса остаются постоянными.

J₁₁=J₂₂, еслиJ₁>J₂ ₂>₁

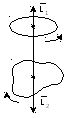
L₁=L₂

§5.6 Вычисление момента инерции.

Теорема Штейнера: Момент инерции тонкого стержня

dJ=dmx²

=m/L– линейная плотность

dm=dx

dJ= x²dx

Моменты инерции тел:

1) Материальная точка J=mR²

2) ОбручJ=mR²

3) Диск (цилиндр) J=1/2mR²

4) Шар J=2/5mR²

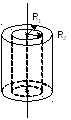
5) Тонкий стержень J=1/12mL²

6) Полый цилиндр J=1/2(R₁²+R₂²)

Если известен момент инерции относительно оси, проходящей через центр инерцииJ₀, то момент инерцииJотносительно другой оси, параллельной первой, можно вычислить по формулеJ=J₀+md²