4. Связь момента силы относительно оси с моментом силы относительно точки

Связь между моментами устанавливается как связь между вектором и его проекцией на соответствующую ось.

Проведем через точку О, где задан момент силы относительно точки декартовы оси координат x, y, z . Момент силы относительно точки можно представить в виде суммы трех векторов . Эти векторы являются моментами силы относительно осей x, y, z соответственно.

Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки на оси.

Формулы для моментов силы относительно осей координат

Если сила задана своими проекциями на оси координат и даны координаты точки приложения этой силы, относительно осей координат, то моменты силы относительно осей координат вычисляется следующим образом:

Лекция 4 Теоремы о сложении двух параллельных и двух антипараллельных сил

1. Две параллельные силы имеют параллельную им равнодействующую, модуль которой равен сумме модулей сил, а линия действия равнодействующей делит расстояние между точками приложения сил внутренним образом на части, обратно пропорциональные их модулям.

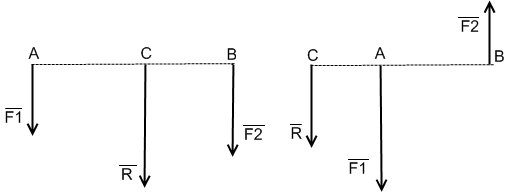
Дано: .

2. Две антипараллельные не равные по модулю силы силы имеют параллельную им равнодействующую, модуль которой равен разности модулей сил, а линия действия равнодействующей делит расстояние между точками приложения сил внешним образом на части, обратно пропорциональные их модулям.

Дано: ( ) .

Пара сил. Момент пары сил

Применяем теорему для случая F1=F2, получим R=0. Такая система сил называется парой сил (ПС). При действии на тело ПС создает вращательный эффект, который характеризуется векторным и алгебраическим моментом.

Парой сил называется система двух равных по модулю, антипараллельных сил, линии действия которых не совпадают.

1. Векторный момент ПС характеризует величину, направление и плоскость действия вращательного эффекта.

Векторным моментом пары сил называется вектор , модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

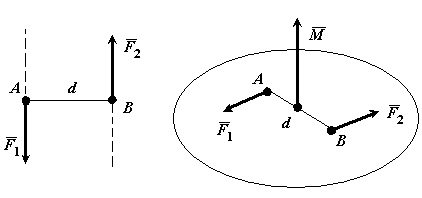
Модуль ПС : .

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы .

,

Момент ПС не зависит от положения точки О, следовательно это свободный вектор. Он может быть приложен в любой точке тела.

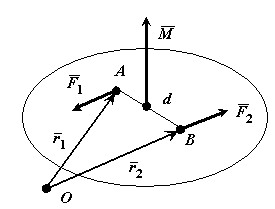
2. Алгебраический момент ПС характеризует величину и направление вращательного эффекта.

Это есть взятое со знаком плюс или минус в зависимости от направления вращения произведение модуля любой силы на плечо ПС.

.

Правило знаков:

Mo

Эквивалентность пар сил

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые вектор-моменты.

Следствие: Не изменяя действие ПС на тело можно:

1. Переносить ПС в любое место плоскости действия.

2. Переносить ПС в любую параллельную плоскость.

3. Одновременно изменять плечо и силы, сохраняя при этом момент пары.

Теорема о сложении пар сил. Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то перенося все вектор-моменты ПС как свободные векторы в одну точку, получим пучок векторов (аналогия -ССС).

Последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

(*)

Аналитический способ определения момента эквивалентной пары

Момент эквивалентной ПС в декартовых координатах определяется следующим образом:

.

Находим проекции вектора, спроецировав векторное равенство (*) на оси координат: .

Модуль равнодействующей ПС и направляющие косинусы:

R = , .

Необходимые и достаточные условия равновесия пар сил

1. Геометрическая форма

Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

2. Аналитическая форма

M = , если . Следовательно, аналитические условия равновесия имеют вид:

1) , 2) , 3) .

Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.