Классификация сил

1.Силы подразделяются на сосредоточенные и распределенные

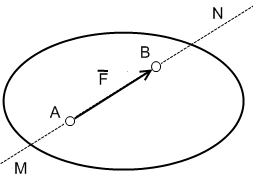
Сосредоточенные силы приложены в одной точке. Силу как величину векторную обозначают какой-либо буквой со знаком вектора (например, или ). Для выражения числового значения силы или ее модуля используется знак модуля от вектора или те же буквы, но без знака вектора (например, и или и ). Характеризуются тремя факторами:

1) Величиной (модулем) - в выбранном масштабе есть длина отрезка АВ. 2) Линией действия – линия MN. 3) Точкой приложения - точка А. В системе СИ сила измеряется в ньютонах = Н.

Распределенные силы действуют на все точки тела (объема, поверхности, линии). Характеризуются интенсивностью распределенной нагрузки q. При расчетах распределенная нагрузка заменяется эквивалентной сосредоточенной силой . Для этого необходимо найти модуль и линию действия силы. Модуль равен площади, ограниченной эпюрой распределенной нагрузки, линия действия проходит через центр тяжести эпюры q. Размерность интенсивности распределенной нагрузки [q] = H/м.

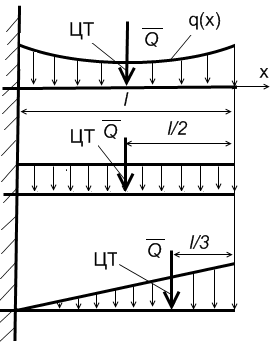
В общем случае: Q = . Частные случаи 1. Равномерно распределенная нагрузка (q=cost). Q = ql. Центр тяжести прямоугольника находится в точке пересечения диагоналей. 2.Нагрузка, распределенная по закону треугольника Q = 0,5ql . Центр тяжести треугольника находится в точке пересечения медиан.

Аксиомы статики

А ксиома о равновесии двух сил. Если свободное абсолютно твердое тело под действием двух сил находится в равновесии, то силы равны по величине и направлены вдоль одной прямой в противоположные стороны.

Аксиома о добавлении (отбрасывании) уравновешенной системы сил. Если на твердое тело действует система сил, то к ней можно добавить (отбросить) уравновешенную систему сил. Полученная после добавления (отбрасывания) новая система сил эквивалентна первоначальной.

Следствие: Сила – вектор скользящий.

А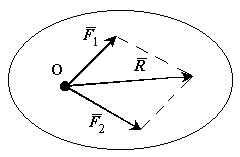 ксиома параллелограмма сил. Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и равную по величине и направлению диагонали параллелограмма, построенного на этих силах, как на сторонах.

Эта аксиома допускает и обратное утверждение:

Силу можно разложить бесчисленным множеством способов на две силы, приложенные в любой точке линии действия данной силы.

А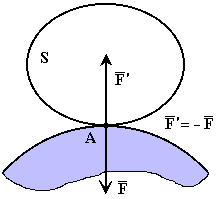 ксиома о равенстве действия и противодействия. При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.

Если к данному телу приложена сила воздействия от другого тела, то от данного тела к другому телу будет приложена сила , равная и прямо противоположная силе . Силы приложены в одной геометрической точке, но к разным телам.

Аксиома отвердевания. Равновесие механической системы не нарушается от наложения новых связей; в частности, равновесие механической системы не нарушится, если все части системы связать между собой неизменно, жестко.

Свободное и несвободное тело. Связи, реакции связей.

Принцип освобождаемости от связей

Свободным твердым телом называется тело, имеющее возможность совершать любое движение из данного положения. Тело не свободно, если его положение в пространстве ограничено другими телами – связями. При решении большинства задач механики приходится иметь дело с телами несвободными, т.е. лишенными возможности перемещаться в направлении действия приложенных к ним активных сил. Связь и тело (объект исследования) взаимодействуют по закону равенства действия и противодействия. Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении, называется реакцией связи. Направление реакции противоположно направлению, в котором тело стремится переместиться под действием активных сил. Эффект от действия связей такой же, как от действия определенных, дополнительных сил, которые могут быть приложены к свободному телу вместо связей. Поэтому в механике применяется следующий принцип.

Принцип освобождаемости от связей. Любое несвободное тело можно считать свободным, если мысленно отбросить наложенные связи, заменив их действие силами-реакциями связей.

П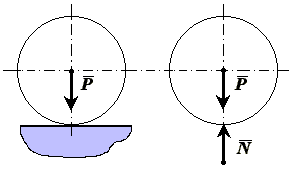 усть, например, на гладкой неподвижной горизонтальной плоскости покоится шар. Плоскость, ограничивающая движение шара, является для него связью. Если мысленно освободить шар от связи, то для удержания его в покое к нему в точке касания с плоскостью нужно приложить силу , равную по модулю весу шара и противоположную ему по направлению. Сила и есть реакция плоскости (реакция связи). Шар, освобожденный от связи, будет свободным телом, на которое действует задаваемая (активная) сила и реакция плоскости .

2. Силы подразделяются на внешние и внутренние

Внешние силы характеризуют действие сил, не входящих в данную механическую систему, внутренние силы – есть силы взаимодействия элементов механической системы.

3.Силы подразделяются на активные (заданные) и реакции связей

Активные силы представляют собой расчетную нагрузку на объект исследования (ОИ). Они могут вызвать движение свободного тела. Величина, направление и точка приложения этих сил известны. Реакции связей характеризуют действие связей на ОИ. Это пассивные силы, они не могут вызвать движение тел, их величина и направление находятся при решении задачи. Активные силы и силы реакции относятся к категории внешних сил.

Основные виды геометрических связей