4. Системное представление физического эксперимента.

С учетом вышеизложенного удобно представить обобщенную схему физического эксперимента в следующем виде (рис.9).

Пусть S – выделенная для исследования в данном эксперименте физическая система. Она находится к началу эксперимента (наблюдения) в некотором состоянии (см. 2), которое определяется некоторым множеством параметров состояния {П}; в их число входят собственные параметры и динамические переменные. Параметры состояния связаны между собой уравнением состояния.

Выделенная физическая система S взаимодействует с окружающей средой (другими системами), в том числе, с экспериментатором. Воздействия на систему могут быть контролируемыми, которые, может задавать и изменять по плану эксперимента сам экспериментатор. Такие воздействия в теории систем называются управляющими, или просто управлениями {U}. Некоторое число (одно или несколько) управляющих воздействий в данном эксперименте являются основными и определяются как входы исследуемой системы.

Воздействия на систему могут быть неконтролируемыми, такими, что их наличие и изменение априори не известно экспериментатору. Обычно неконтролируемые воздействия {ξ} считаются мешающими, искажающими результаты эксперимента, поэтому их пытаются устранить, или существенно уменьшить (например, экранированием от электромагнитных помех), либо стабилизировать (например, поддерживать температуру окружающей среды постоянной). В то же время, при исследовании системы на помехоустойчивость, те же специально создаваемые (генерируемые) электрические помехи будут представлять одно из управлений {U}.

В процессе существования физической системы могут изменяться и её собственные параметры {П}. Как правило, эти изменения несут случайный характер и называются флуктуациями.

Физическая система реагирует на управляющие воздействия {U} и {ξ} и флуктуации {ΔП} определенным образом, т.е. эволюционирует во времени, изменяя свое состояние. Об этом процессе можно судить, наблюдая и фиксируя изменение какого-либо параметра П_i (или нескольких параметров) состояния, связанных с воздействием U_i - входом системы (его принять обозначать Х). Параметр П_i в этом случае считается выходом системы Y. Таким образом

Y(t) = F[{П}, {U}, X, t]. (1)

Здесь t – текущее время.

Зависимость (1) и подлежит изучению в некотором конкретном эксперименте.

К онтролируемые (управляющие) Неконтролируемые («мешающие»)

воздействия {U} на воздействия { } на

физическую систему физическую систему (помехи)

{ΔП} {П}

Вход Х Выход Y

Флуктуации параметров

самой физической системы Исследуемая физическая

система S

Рисунок 9. Обобщенная схема физического эксперимента.

Итак, в процессе экспериментального исследования физической системы выделяют:

• { } – это неконтролируемые («мешающие») изменения в процессе эксперимента температуры, влажности, давления, освещенности, электромагнитного и радиационного фона - помехи.

• {U} Контролируемые (управляющие) воздействия – это передача физической системе (отбор у нее) вещества, энергии; передача ей информации посредством физического носителя (сигнала).

• {ΔП} – неконтролируемые изменения собственных параметров системы – флуктуации.

• Х – вход - управляющее воздействие, вызывающее исследуемую в данном опыте реакцию физической системы – выход Y - т.е. исследуемую зависимость (1).

• Y – выход – представляет собой реакцию физической системы на:

- вход и другие управляющие воздействия, помехи и флуктуации.

Примеры постановки целей эксперимента:

а) Для физической системы «идеальный газ» её состояние определяют такие физические величины, как абсолютная температура Т, давление р, объем V. Зависимость между параметрами системы задается уравнением её состояния. Для упомянутой системы «идеальный газ» уравнение состояния есть уравнение Менделеева-Клапейрона, (связывающее) перечисленные параметры Т, р, V:

, (1)

где m – масса газа, μ – его молярная масса, R – универсальная газовая постоянная.

Пусть, например, исследуется зависимость давления р идеального газа от температуры Т при постоянной массе (m = const), составе (μ = const) и объеме газа (V=const). (Такой процесс называется изохорным). Уравнение (1) для этого эксперимента имеет вид

, (2)

где ,

Тогда исследуемая зависимость имеет линейный характер р=КТ.

Типовой график исследуемой зависимости имеет вид (рисунок 10).

р

α

0 Т

Рисунок 10. Типовой график изохорного процесса.

Целью эксперимента может являться подтверждение справедливости теоретически выдвинутой гипотезы, выражений формулы (2) и рис. 10.

b) Уравнение состояния для простейшей механической системы – движущейся материальной точки (частицы) задается вторым законом Ньютона:

, (3)

где m – масса частицы; - равнодействующая сил, приложенных к частице, - приобретенное частицей под действием силы ускорение.

Здесь в эксперименте могут быть исследованы, например:

- зависимость ускорения от массы при постоянной силе .

- зависимость ускорения от силы при постоянной массе частицы.

Цель эксперимента может быть сформулирована как экспериментальное подтверждение 2-го закона Ньютона.

Математически простые уравнения состояния, подобные приведенным выше, могут быть получены только при значительном упрощении реальных систем, замене их идеализированными моделями.

В реальном эксперименте практически всегда приходится ограничивать задачи исследования физической системы определением небольшого количества её параметров и выяснением зависимостей между параметрами состояния системы, воздействиями на нее (управлениями, возмущениями, флуктуациями) и реакцией системы на эти воздействия.

Влиянием других внешних воздействий на систему как правило пренебрегают, считая их весьма малыми или неизменными.

В любом случае при исследовании физической системы экспериментатор вынужден не только ограничивать количество интересующих его параметров и функциональных связей, но и действовать в рамках некоторого ограниченного пространства и какого-то ограниченного промежутка времени (т.е., «здесь и сейчас»).

Пример системного подхода к организации физического эксперимента с простейшим объектом исследования – электрическим сопротивлением R, резистором.

Напомним кратко и очень схематично основные сведения из классической теории электропроводности металлов, известные из школьного курса физики.

В некотором объеме металла (проводе), организованном в виде кристаллической решетки, имеется достаточно большое число хаотически движущихся коллективизированных электронов. При наложении на образец металла электрического поля электроны начинают двигаться («дрейфовать») в направлении, противоположном полю, создавая электрический ток. Сила тока тем больше, чем больше разность электрических потенциалов U на концах металлического провода и чем меньше плотность «упаковки» ионов металла в кристаллической решетке. Зависимость силы тока I, разности потенциалов (электрического напряжения) U и сопротивления проводника R выражены в законе Ома для участка цепи:

.

Электрическое сопротивление R проводника длиной ℓ, площадью поперечного сечения S определяется как

где ρ – удельное электрическое сопротивление данного металла.

В металле происходят столкновения движущихся электронов с ионами узлами кристаллической решетки, электроны тормозятся и отдают свою кинетическую энергию в виде тепла. Этот физический эффект формализован в законе Джоуля-Ленца:

,

где I – сила тока в проводнике, R – его электрическое сопротивление, ∆t – время протекания тока, Q – количество теплоты, выделяющееся в проводнике за это время.

И закон Ома, и закон Джоуля-Ленца являются надежно установленными законами физики, однако не так уж давно они имели статус научных гипотез и нуждались в экспериментальной проверке.

Поскольку электрическое сопротивление R является пассивной физической величиной, для его и измерения необходимы активные вещества в виде электрического тока, протекающего через резистор, и соответствующего ему падения напряжения U.

В учебных целях воспроизведем некоторые эксперименты по исследованию проводимости в металлах.

Для опытов используем проволочные резисторы R выполненные в виде спиралей с различным числом витков проводов из различных металлов (форма спирали используется только для уменьшения габаритов резистора), источник э.д.с, измерительные приборы (амперметр и вольтметр) и ключ Кл для замыкания и размыкания цепи. Перечисленные элементы входят в набор «Электричество – 1», выпускаемый фирмой «L – микро».

Общая принципиальная схема экспериментов с резистором R приведена на рисунке 11.

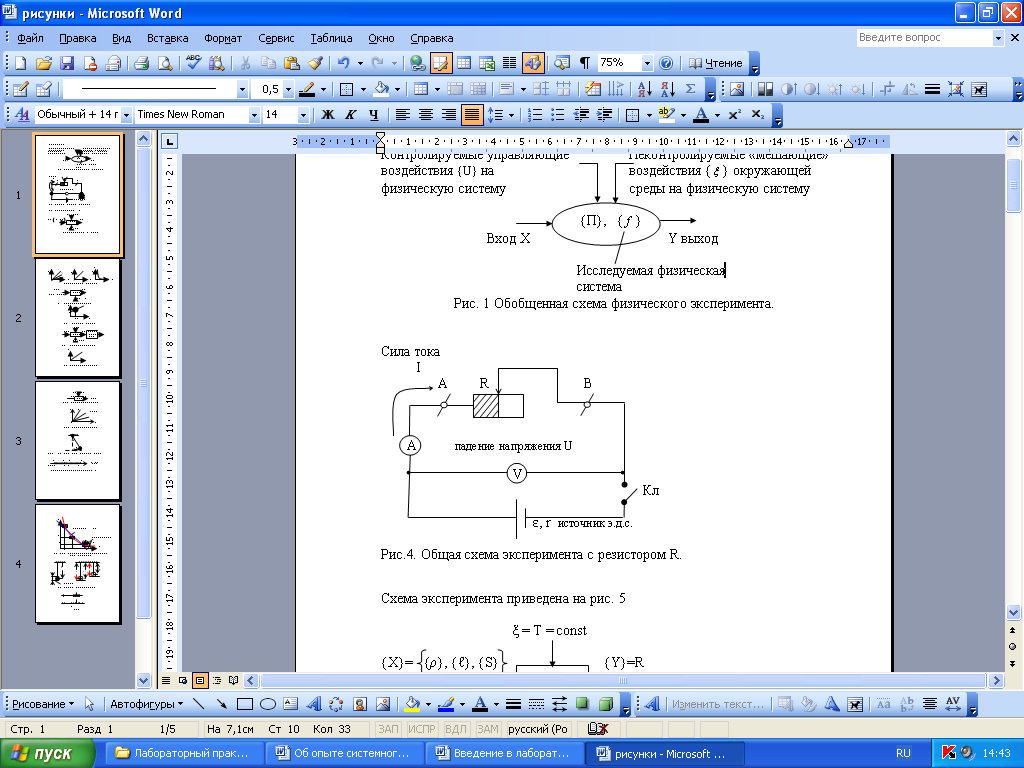
Рисунок 11. Общая схема экспериментов с резистором R.

Экспериментальное задание №1. Исследование зависимости сопротивления R резистора от его геометрических размеров проводника (длины ℓ и площади поперечного сечения S) и материала (удельного сопротивления ρ металла).

Проверяемая гипотеза состоит в том, что электрическое сопротивление R провода прямо пропорционально его длине ℓ, обратно пропорционально площади S поперечного сечения провода, а также зависит от вида металла (его удельного сопротивления ; предположим, что это прямопропорциональная, т.е. линейная зависимость).

Математически гипотезу отражает формула

~ .

Предполагаем, что температура Т резистора (мешающий фактор в данном опыте) поддерживается неизменной в течении опыта, и сила тока I через резистор задается постоянной.

,

Блочная схема эксперимента приведена на рисунке 12.

{ξ}: Т = const

{Х}= {ρ}, {ℓ}, {S} {Y}=R

резистор

{U}: I = const

Рисунок 12. Блочная схема эксперимента для задания 1.

Экспериментально снимаются следующие зависимости:

1.1. , при ℓ, S = const – разные материалы проволоки ( );

1.2. , при S, ρ = const – разная длина проволоки ( );

1.3. , при ρ, ℓ = const – разный диаметр, т.е. разная площадь поперечного сечения проволоки ( ).

На рис. 13. приведены типовые графики этих зависимостей:

ρ₁>ρ₂>ρ₃

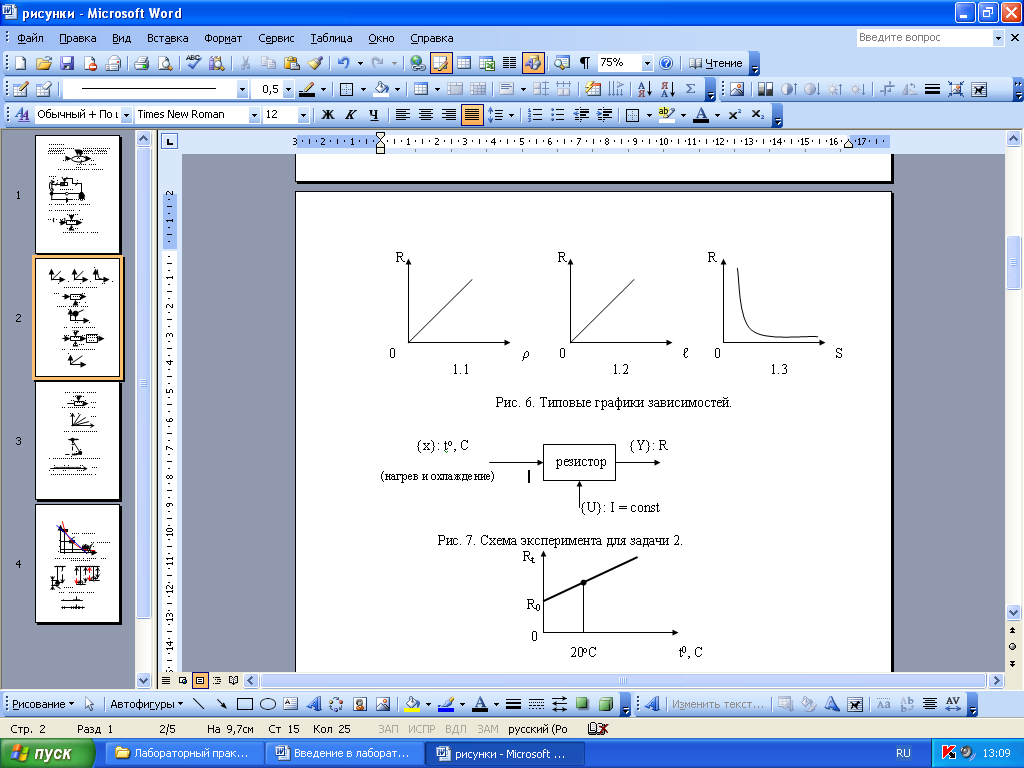
Рисунок 13. Типовые графики зависимостей.

Задание 2. Исследование зависимости сопротивления R резистора от его температуры

Схема эксперимента приведена на рисунке 14.

Нам известно, что зависимость R(t) из теоретических соображений имеет вид:

,

где R_t – сопротивление резистора при данной температуре t (по шкале Цельсия);

R₀ – сопротивление резистора при температуре t₀=20^оC;

α – температурный коэффициент сопротивления, .

Эта формула отражает гипотезу, которая в учебных целях должна быть «проведена», т.е. подтверждена или отвергнута на основании результатов эксперимента.

Геометрические параметры провода резистора (ℓ, S) и материал (ρ), из которого он сделан, сохраняются постоянными.

В эксперименте снимается зависимость R(t^о) (см. график рис. 15).

Может быть определено значение α, например, для терморезисторов.

{Х}: t^о, С резистор Y: R

(нагрев и охлаждение)

{U}: I = const

Входом является температура t^о резистора, выходом – его сопротивление R.

Рисунок 14 - Схема эксперимента для задания 2.

R_t

α

R₀

0

t₀=20 ^оС t, ⁰С

Рисунок 15. Типовой график зависимости R = f (t^o,C).

Задание 3. Исследование теплового действия электрического тока (эффект Джоуля-Ленца)

При протекании через резистор с сопротивлением R электрического тока силой I в резисторе за время ∆t выделяется количество теплоты Q:

.

Эта «гипотеза» исследуется как зависимость Q(R) при I = const, ∆t = const по схеме рис. 16.

{ П} : R

Y : Q Измеритель

{Х}: R резистор количества

теплоты

{U}: Δt = const

Рисунок 16. Схема эксперимента для задания 3.

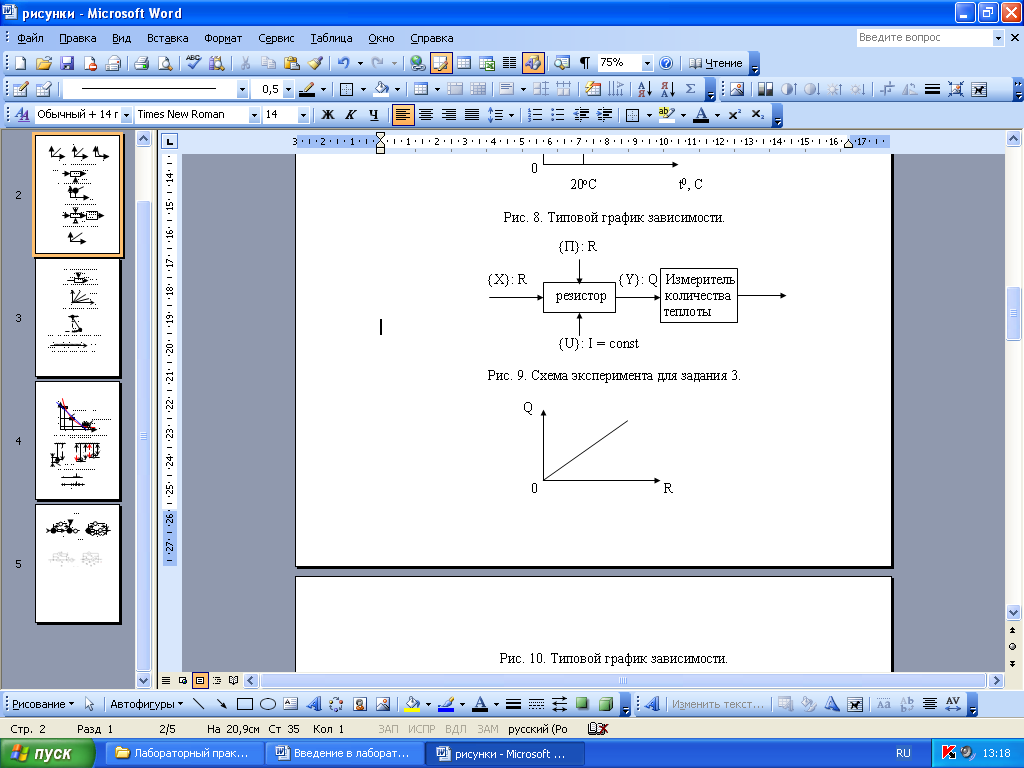
Рисунок 17. Типовой график зависимости Q = f (R).

Задание 4. Исследование зависимости падения напряжения ∆V на резисторе от его сопротивления (закон Ома для участка цепи):

Принципиальная схема эксперимента приведена на рис. 11.

Рис. 10. Типовой график зависимости.

{ ξ}: Т = const

{Х}: I {П}: R

резистор {Y}: ∆V

Рисунок 18. Схема эксперимента для задания 4.

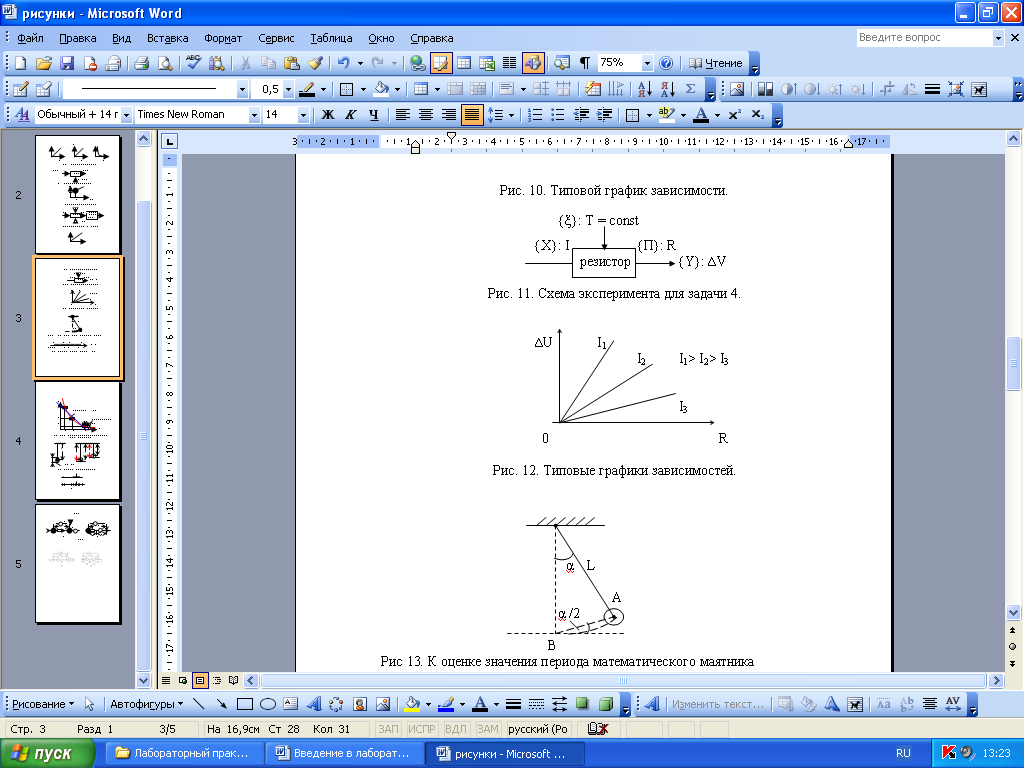
Рисунок 19. Типовые графики зависимостей.

Таким образом, цели и задачи экспериментального исследования даже в случае простой физической системы как объекта исследования могут быть различными, как и схема проведения эксперимента.

При наличии нескольких входов {Х}=х₁,х₂,…,х_n, эксперимент является многофакторным.

В многофакторном эксперименте исследователь варьирует несколькими параметрами, влияющими на исследуемую систему.