1.3.2. Виды состояния физической системы

Если какой-либо параметр состояния системы постоянен во времени, то состояние системы, определяемое именно этим параметром состояния называют равновесным. Равновесное состояние системы, все параметры состояния которой постоянны во времени, называют стационарным, или установившимся.

Равновесное состояние физической системы нарушается при воздействии на нее со стороны окружающей среды (соседних систем) или случайных изменений (флуктуаций) собственных параметров. В результате система может придти к новому равновесному состоянию, но уже с другими значениями параметров состояния. Процесс изменения состояния системы называется переходным.

Если система, будучи выведенной из равновесного состояния одноразовым воздействием, самостоятельно возвращается в исходное состояние, то это состояние устойчивого равновесия. Если малое, даже случайное воздействие (флуктуация) приводит систему к выходу из равновесного состояния, к которому система уже не может вернуться самостоятельно, то это состояние неустойчивого равновесия.

2. Эволюция (поведение) системы

Движение физической системы, т.е. последовательный переход физической системы из одного состояния в другое, называется эволюцией (говорят, что система обладает поведением).

Под поведением системы понимается:

- в широком смысле - любое изменение состояния системы (как реакция на внешние воздействия или изменение собственных параметров);

- в узком смысле – осуществленный самой системой комплекс целесообразных действий, включающий выбор оптимальных решений с целью реализации определённой «системной» функции и осуществление приводящих к цели действий, с максимальной вероятностью и наименьшими затратами приводящий к достижению цели.

У природных физических систем цель как таковая принципиально отсутствует. Направление поведения физической системы определяет фундаментальный закон природы: принцип Ле Шателье-Брауна. Его суть в том, что внешние вещественные, энергетические, информационные воздействия окружающей среды на физическую систему или внутренние флуктуации (возмущения), выводящие систему из состояния равновесия, вызывают ее определенные реакции, проявляющиеся в изменении состояния системы и/или выработке ей ответных воздействий на среду и на самое себя с целью устранения (уменьшения) внешних воздействий и внутренних возмущений. В этом проявляется консерватизм как фундаментальное свойство природы. Таким образом, свободная физическая система как бы сама «определяет» своё поведение. При взаимодействии с другими системами поведение данной системы зависит также и от их состояния в момент начала взаимодействия и в его процессе.

Эти реальные явления происходят во времени, следовательно, являются процессами.

Порядок и направление прохождения процессов изменения состояния системы устанавливается двумя диалектическими принципами: детерминизмом и причинностью.

Суть этих принципов состоит в следующем:

- ни одно реальное явление не возникает самопроизвольно. Всегда имеется причина – предшествующее ему по времени другое реальное явление, которое его вызывает; при этом ни одно явление, произошедшее в данный момент времени, не зависит от того, какие явления произойдут после него (причинность);

- реализация данного явления обусловлена совокупностью определённых оснований для реализации именно этого, а не какого-то другого явления (детерминизм).

Процесс-причина называется в теории систем входным, или просто входом для данной системы, а процесс-следствие – выходом.

Зависимость выхода от входа однозначно определяется состоянием системы в данный момент времени.

Вообще говоря, любая неоднородность распределения в пространстве и времени вещества, энергии, информации вызывает реакцию системы, движение, в котором могут изменяться параметры состояния системы и динамические переменные. Формально направленность движения определяет математическая конструкция, называемая градиентом (grad).

Простейший случай реакции физической системы – пассивное сопротивление, инерционность. Тело «сопротивляется» попыткам изменить (ускорить или замедлить) состояние его движения. Мерой инертности является инерционная масса. Аналогично, в катушке индуктивности, находящейся в изменяющемся магнитном поле, наводится ЭДС самоиндукции, создающая в катушке ток, образующий собственное магнитное поле, компенсирующее изменение внешнего поля (правило Ленца, «минус» в формуле закона электромагнитной индукции Фарадея). Более сложное поведение- поддержание устойчивого равновесного состояния без воздействия на пытающиеся его изменить факторы. Такое поведение можно определить как активное сопротивление самой системы, заключающиеся в определённом изменении её динамических переменных. В живых системах такое поведение называется гомеостазом. Для биологических и социальных сложных систем характерна реакция в виде устранения (изменения) факторов, стремящихся изменить ее состояние.

Поведение системы математически описывается уравнением (законом) движения. Это уравнение имеет смысл отображения, которое каждому входу и каждому состоянию физической системы ставит в соответствие определённый выход. Таким образом, систему характеризуют первичные понятия входа, состояния и выхода, а также отношение между входом и состоянием (переходное отображение) и отношение между состоянием и выходом (отношение выхода). Знание этих характеристик необходимо для описания поведения системы, предсказания ее поведения и указания способов обеспечения заданного (требуемого, желательного поведения) системы.

Уравнение движения представляет собой математическое выражение связи между состояниями системы в различные моменты времени. Другими словами, это уравнение описывает физический процесс изменения во времени параметров состояния физической системы.

Любой физический процесс характеризуется изменением каких-либо физических величин, связанных между собой. Необходимая и устойчивая связь (зависимость) между определенными физическими величинами фиксируется как физический закон.

Так, для классической механической системы уравнением движения является 2-й закон Ньютона, для классической электродинамической системы – роль уравнений движения играют уравнения Максвелла, для квантовой системы - уравнение Шрёдингера. Законы сохранения относят к уравнениям эволюции в том смысле что они постулируют неизменность в процессе эволюции системы некоторых её собственных параметров и динамических переменных - энергии, электрического заряда импульса, момента импульса, электрического заряда и др.

Важным для любого физического закона являются условия и границы его применимости. Существуют, например, правила запрета – физические законы, устанавливающие принципиальную невозможность определенных состояний физических систем или существование количественных ограничений на значения их параметров.

Рассмотрим описания поведения системы в некоторых фундаментальных физических теориях.

Классическая механика. В классической механике - механике системы материальных точек (частиц) - начальные условия задаются совокупностью координат и импульсов, (или скоростей) всех частиц. Эти величины могут принимать произвольные значения: положение и импульс любой частицы не зависят от положений и импульсов всех других частиц.

Уравнением движения является второй закон Ньютона. Начальные условия вместе с законом движения полностью определяют поведение объектов, рассматриваемых в классической механике. Уравнения движения частиц определяют ускорения частиц в зависимости от приложенных к ним сил. Силы являются однозначными функциями расстояний между частицами и их относительных скоростей.

Координаты и импульсы (или скорости) - основные физические величины в механике Ньютона, так как определяют состояние системы. Все остальные механические величины - энергия, момент импульса, действие и др., выражаются в виде функций координат и импульсов.

Рассмотрим в качестве примера механическую систему, состоящую из нескольких частиц. Система локализована в некоторой области пространства и существует во времени. Её поведение заключается в движении (изменении положения). Положение механической системы в пространстве в выбранной системе координат характеризуется радиус-векторами каждой частицы (или, например, в декартовой системе координат – тройками ортогональных координат).

Состояние механической системы в дополнение к координатам характеризуется также векторами скоростей каждой частицы (или тройками их проекций на ортогональные оси координат).

Физические величины – координаты и скорости – суть параметры состояния механической системы. Зная параметры состояния можно с помощью уравнения движения (2-го закона Ньютона) определить поведение, или эволюцию системы во времени.

Термодинамика. Эволюция реальных систем во времени фактически не рассматривается. Можно лишь установить однозначные связи между термодинамическими параметрами различных равновесных состояний.

Неравновесные процессы изучаются в термодинамике необратимых процессов. В этой теории состояние системы характеризуется локальными термодинамическими функциями координат и времени. К их числу относятся: плотность массы, плотность импульса, температура, давление, плотность внутренней энергии или энтропии. Законы сохранения массы, импульса и энергии в движущейся среде формируются как уравнения переноса. Эти уравнения совместно с уравнением состояния и калорическим уравнением, дающим зависимость энергии от давления и температуры, позволяют по начальным значениям локальных термодинамических функций проследить их эволюцию во времени.

Квантовая механика. Эволюцию состояния квантовой системы однозначно определяет временное уравнение Шредингера. Уравнение, описывающее неравновесные процессы в квантовой системе, носит название основного кинетического уравнения.

Интегрируя основное кинетическое уравнение по всем переменным {квантовым числам), можно получить квантовые кинетические уравнения того же типа, что и классическое уравнение Больцмана.

Для представления поведения физической системы наряду с уравнениями движения используется фазовое пространство. Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной физической системы представляется в нём одной единственной точкой, а эволюция этой системы – перемещением этой точки.

Координатами фазового пространства в случае механических систем являются пространственные координаты частиц системы и их импульсы.

Например, фазовое пространство для системы, состоящей из одной свободной частицы, имеет 6 измерений, в числе которых –три пространственные координаты, а ещё три – ортогональные компоненты вектора импульса частицы.

Размерность фазового пространства может быть различной. Двумерное фазовое пространство называется фазовой плоскостью.

Рассмотрим в качестве примера представление на фазовой плоскости некоторых колебательных систем (осцилляторов). На оси абсцисс фазовой плоскости откладываются значение переменной величины х, а на оси ординат – первая производная х по времени.

Представим на фазовой плоскости поведение линейного осциллятора без потерь, например, LC-контура (рис. 7, а) . Это консервативная колебательная система.

Переменная величина – заряд q на конденсаторе; колебания гармонические. Обозначим ; .

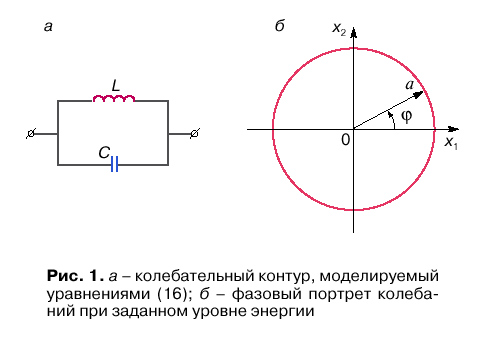
Рисунок 7. Представление на фазовой плоскости гармонических колебаний в LC-контуре.

Фазовый портрет консервативной колебательной системы (рис. 7, б) представляет собой окружность радиуса a с центром в начале координат. Параметр а имеет смысл полной энергии электромагнитного поля конденсатора и катушки индуктивности ( ).

Линейный осциллятор с потерями (с затуханием) – линейной диссипативной осциллятор; сила трения пропорциональна скорости изменения переменной величины. Пример такой системы – колебательный LC-контур, содержащий активное сопротивление R. Уравнение колебаний

   

заменой переменных сводится к безразмерной форме

 ,  ,   .

Параметр δ имеет смысл коэффициента трения.

При δ = 0 имеем линейный осциллятор, без потерь, рассмотренный выше. Учет трения качественно меняет фазовый портрет системы. Для 0 < δ < 1 решением уравнения колебаний является

, ,

где A и – произвольные постоянные, имеющие смысл амплитуды и фазы колебаний и определяемые начальными условиями. На фазовой плоскости для любых начальных условий имеют место скручивающиеся спирали, (рис. 8, а), по которым фазовые точки асимптотически приближаются к началу координат, характеризуя затухающий колебательный процесс. Нуль координат является особой точкой системы, которая в случае δ<1 есть устойчивый фокус.

Если коэффициент трения δ>1, процесс в системе апериодический:

, где

.

Ф азовые траектории выглядят как семейство характерных кривых, по которым, как и в предыдущем случае, изображающие точки стремятся к нулю координат (рис. 8, б). Особая точка в указанных условиях есть устойчивый узел.

а б

Рисунок 8. Фазовые портреты колебаний в осцилляторах с потерями: а) затухающие колебания;

б) затухание.

Таким образом, из фазовых портретов (рис. 8) следует, что при любых значениях физических параметров системы (если δ>0), диссипативный маятник характеризуется единственным устойчивым состоянием равновесия в нуле фазовых координат. Независимо от выбора начальных условий наблюдается затухающее колебательное или апериодическое движение. С течением времени (при t → ∞) любая изображающая точка стремится к началу координат в устойчивый фокус либо узел.