3. Приведение параметров механических частей электропривода к входному звену

Ставится задача получения формулы для приведенного момента инерции механической части электропривода, который содержит элементы, часть которых участвует во вращательном, а часть – в поступательном движениях. Сложность возникает тогда, когда необходимо записать уравнения либо для поступательного, либо для вращательного движения (т.е. нужно приводить момент инерций к массе или наоборот).

Рассмотрим переход от реальной схемы рис.2.2 к эквивалентной схеме рис.2.3. При этом приведенный и реальный ЭП должны иметь одинаковые момент сопротивления М_с, момент инерции J и угловую скорость  вращения ротора электродвигателя.

Приведение расчетных параметров электропривода рассмотрим на основе приводимого ниже примера:

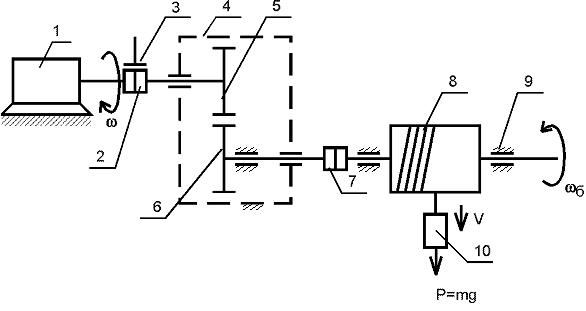
Рис. 2.2 Схема реального ЭП подъемного устройства

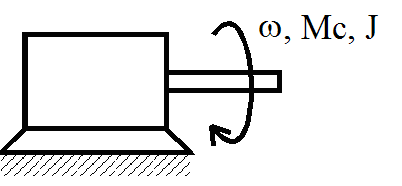
Рис. 2.3 Схема эквивалентного ЭП подъемного устройства

На рис.2.2 изображена реальная схема ЭП, на рис. 2.3 – эквивалентная схема. На рис. 2.2 приняты следующие обозначения:

1 – электродвигатель; 2 –муфта; 3 – тормозное устройство; 4 – корпус редуктора; 5,6 – зубчатые колеса; 7 – муфта; 8 – барабан; 9 – корпус устройства; 10 – груз;  – угловая скорость вращения вала двигателя; _б – угловая скорость вращения барабана (угловая скорость на выходном валу ЭП); V – линейная скорость перемещения груза; Р – вес груза.

Элементы 4,5,6 образуют редуктор, в целом же схема рис. 2.2 является схемой подъемного устройства.

На рис. 2.3 приняты обозначения:

J – приведенный момент инерции; М_С – приведенный момент нагрузки.

При подаче напряжения питания на обмотку управления электродвигателя 1 начинается вращение его ротора, в силу чего приводится в движение барабан 8, который осуществляет подъём груза.

Приняты допущения, что все элементы кинематической схемы рис. 2.2 являются абсолютно недеформируемыми, но трос может изгибаться идеально. В качестве звена приведения обычно берут вал двигателя 1.

4. Приведение моментов инерции

Запишем выражение для кинетической энергии реальной и эквивалентной схем (рис. 2.2 и 2.3) и приравняем их друг к другу:

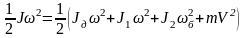, (2.9)

где J_д – момент инерции ротора электродвигателя 1; J₁ – момент инерции вращающихся частей на первичном валу; J₂ – момент инерции вращающихся частей на вторичном валу; m – масса груза.

Деля формулу (2.9) на 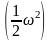, получаем:

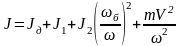. (2.10)

Для приведения параметров движения к входному звену введем передаточное отношение:

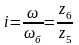, (2.11)

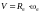, (2.12)

где R_б – радиус барабана.

Выражение для приведенного радиуса инерции будет иметь вид:

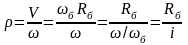. (2.13)

Подставим выражения (2.11)-(2.13) в соотношение (2.10)

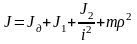. (2.14)

Формула (2.14) позволяет определить момент инерции с учетом масс подвижных частей сложной схемы (рис. 2.2) и перейти к приведенному моменту инерции эквивалентной схемы (рис. 2.3).

5. Приведение моментов сопротивления

Для приведения моментов сопротивления к входному звену воспользуемся формулой для мощности N для эквивалентной схемы (рис. 2.3) и для N_б на валу барабана исходной схемы (рис. 2.2):

, (2.15)

, (2.16)

где R_б – радиус барабана.

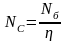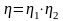, , (2.17)

где 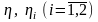– КПД общий, а также редуктора и барабана.

Приравнивая правые части выражений (2.15) и (2.16), с учетом (2.17) получаем:

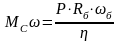; (2.18)

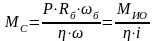, (2.19)

где 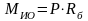– момент нагрузки на исполнительном органе.

В результате получаем следующее дифференциальное уравнение движения для ротора приведенного ЭП:

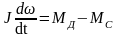, (2.20)

где приведенные: J –момент инерции, М_С – момент сопротивления; М_Д – момент двигателя (описывается для каждого типа двигателя согласно его электрической и физической схемам).