20. Что такое математическое ожидание, дисперсия случайной величины?

Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности: М(Х) = Х1Р1 + Х2Р2 + … + ХпРп . Если число возможных значений случайной величины бесконечно, то , если полученный ряд сходится абсолютно.

Если случайная величина  имеет математическое ожидание M ,то дисперсией случайной величины  называется величина D = M( - M )².

21. Что представляет правило трех сигм?

Практически достоверно, что при однократном испытании отклонение нормально распределенной случайной величины от ее математического ожидания не превышает утроенного среднего квадратического отклонения.

22. Дайте определение генеральной совокупности, выборке.

Вся исследуемая совокупность однородных объектов называется генеральной совокупностью.

Множество из n объектов, отобранных случайным образом из генеральной совокупности, называется выборочной совокупностью или выборкой.

23. Что такое распределение выборки, графическое представление распределений.

24. Что представляет собой эмпирическая ф-ция распределения?

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х

F*(x)=n_х/n, где n_х – число вариант, меньшее х, n – объем выборки

25. Укажите основные числовые хар-ки выборки: среднее арифметическое, мода, медиана…..

 Среднее арифметическое – такое значение признака, сумма отклонений от которого выборочных значений признака равна нулю (с учетом знака отклонения).

Медианой (Ме) называется такое значение признака X, когда ровно половина значений экспериментальных данных меньше ее, а вторая половина — больше.

. Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто.

 Размах вариации – разность между максимальной и минимальной вариантами выборки

Дисперсией называется средний квадрат отклонения значений признака от среднего арифметического. Дисперсия, вычисляемая но выборочным данным, называется выборочной дисперсией и обозначается  .

 Стандартным отклонением (или средним квадратическим отклонением) называется корень квадратный из дисперсии:         

- коэффициентом вариации. - коэффициент осцилляции

коэффициент эксцесса  .                           

26. Что такое точечное оценивание? Приведите св-ва точечных оценок, оценки математического ожидания, дисперсии.

Выборочная оценка параметра, представляющая собой число, называется точечной оценкой.

1. Выборка - последовательность результатов измерений значений случайной величины.

2. 2. Статистическая оценка - приближенное значение вероятностных характеристик законов распределения, полученных на основе статистических или выборочных данных. Точечная статистическая оценка - статистическая оценка, выражаемая одним числом.

3. Статистическая оценка называется несмещенной, если

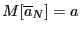
4. Точечная оценка называется состоятельной, если

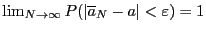
5. Точечная оценка называется сильно состоятельной, если

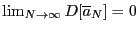
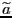6. Точечная оценка называется эффективной, если где все возможные точечные оценки.

7. Точечная оценка называется асимптотически эффективной, если

где все возможные точечные оценки. Пример: выборочное математическое ожидание.