3.3. Дифференциальные уравнения движения системы

Рассмотрим механическую систему, состоящую из n материальных точек M_i c массами m_i (i = 1, 2, …, n), на каждую из которых действует равнодействующая внешних F_i^(e) и внутренних F_i⁽ⁱ⁾ сил.

Для каждой точки системы можно записать основное уравнение динамики:

m_ia_i = F_i^(e) + F_i⁽ⁱ⁾ , (i = 1, 2, …, n). (3.4)

Проектируя каждое из уравнений (3.4) на оси координат, получим систему 3n дифференциальных уравнений второго порядка, описывающих движение системы:

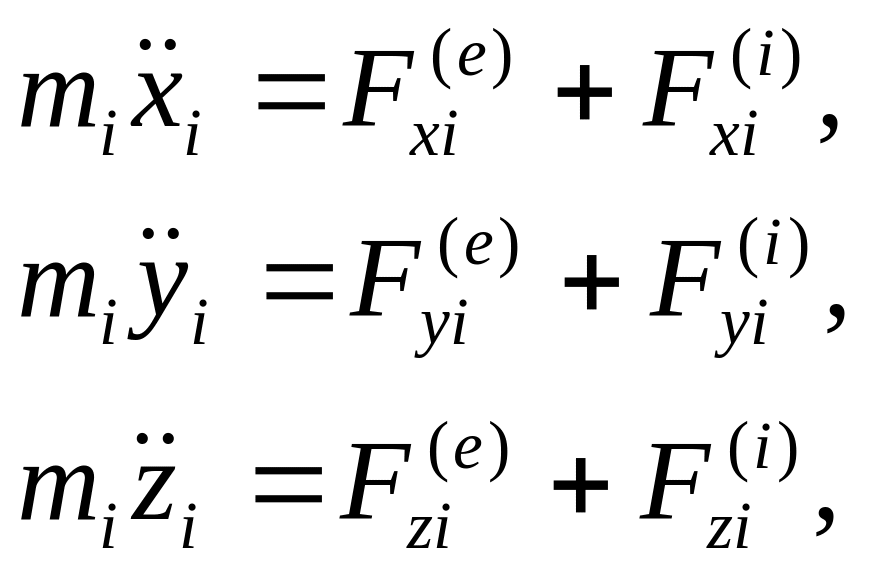
(3.5)

(i = 1, 2, …, n).

Эти уравнения и называются дифференциальными уравнениями движения системы. Вместе с соответствующими начальными условиями они образуют задачу Коши, решив которую, мы найдем закон движения механической системы.

О том, насколько сложной является поставленная задача можно судить хотя бы по тому, что к настоящему времени в общем виде она решена только для n = 2.

Как же изучать движение систем с большим числом степеней свободы и систем с распределенными параметрами, у которых число степеней свободы равно бесконечности?

Во-первых, для решения уравнений (3.5) остаются численные методы, и каждый раз, например, такую задачу решают при стыковке космического корабля с орбитальной станцией.

Во-вторых, очень часто нет необходимости в детальном исследовании движения каждой точки системы и достаточно знания некоторых его интегральных характеристик. Например, при изучении движения потока жидкости или газа.

Эффективным методом исследования движения механических систем является применение общих теорем динамики.

Для реализации этого подхода нужно уметь описывать:

– конфигурацию и распределение масс точек системы в пространстве, что носит условное название геометрии масс;

– движение центра масс системы;

– движение точек системы вокруг центра масс.

К изучению этих вопросов мы переходим и будем их рассматривать в четырех последующих главах.

Примечание:

В динамике механических систем, как и в динамике точки, можно говорить о постановке первой и второй задачи динамики. Однако если при решении второй задачи для точки трудности начинаются только с вычисления первого интеграла – закона изменения скорости, то в динамике систем сложности могут возникнуть уже на стадии определения ускорений тел, входящих в систему.

Глава 4. Геометрия масс системы

Как известно из курса сопромата, прочность балки зависит не только от материала, из которого она изготовлена и площади поперечного сечения, но и от формы этого сечения. Момент сопротивления – основная геометрическая характеристика прочности балки – зависит от момента инерции ее сечения.

Аналогично динамические характеристики механической системы могут определяться законом распределения масс этой системы в пространстве.

4.1. Центр масс системы

Рассмотрим механическую систему, состоящую из n материальных точек M_i (рис. 4.1) c массами m_i (i = 1, 2, …, n).

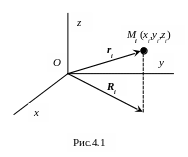
Определение. Центром масс системы называется точка C с радиус-вектором:

r_c = (m_i r_i)/(m_i) . (4.1)

Проектируя на оси Oxyz, получим координаты центра масс системы:

x_c = (m_i x_i)/M,

y_c = (m_i y_i)/M, (4.2)

z_c = (m_i z_i)/M,

где M = m_i – масса системы.

Если точки системы сплошь заполняют некоторый объем V, образуя твердое тело, из формулы (4.1) получим выражение радиус-вектора центра масс этого тела:

r_c = (1/M)_V rdm, (4.3)

где M = _V dm – масса тела.

Проектируя (4.3) на оси Oxyz , получим координаты центра масс этого тела:

x_c = (1/M)_V xdm,

y_c = (1/M)_V ydm, (4.4)

z_c = (1/M)_V zdm.

При этом, очевидно, центр масс тела совпадает с его центром тяжести.