3.2. Степени свободы системы
Как уже было отмечено, точки системы с наложенными на них связями, являются несвободными.
Определение. Степенью свободы голономной системы, называется минимальное число параметров – s, определяющих положение системы в пространстве.
Для точки на плоскости s = 2, и в качестве параметров можно выбрать ее декартовы координаты, а система N точек на плоскости будет иметь 2N степеней свободы.
Если две свободные точки на плоскости (s = 4) соединить стержнем, получим систему с тремя степенями свободы и естественно предположить, что всякое наложение дополнительной связи уменьшает степень свободы системы на единицу.
Поэтому число степеней свободы плоской статически определимой фермы можно найти по формуле:
s = 2У – С – СО , (3.3)
где У – число узлов (шарниров) фермы, С – число ее стержней, а СО – число опорных связей.
Чтобы однозначно определить положение плоской фигуры нужно задать уже три параметра: координаты полюса A - xA , yA и угол ее поворота вокруг этого полюса – j.
На практике бывает удобнее пользоваться другим определением, эквивалентным предыдущему:
Определение. Степень свободы системы s равна минимальному числу дополнительных связей, превращающих ее в неподвижную систему.
При определении числа степеней свободы системы необходимо проанализировать ее структуру, уточнить какие связи в явной или неявной форме уже наложены на систему и какие возможные перемещения системы они допускают. Эти условия надо соблюдать и при наложении дополнительных связей.
Пример 3.1. Определить число степеней свободы фермы (рис. 3.1).
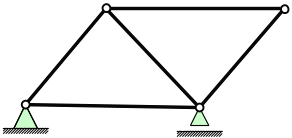
Рис. 3.1
Решение. Число узлов фермы – 4, число ее стержней – 5, число опорных связей – 3. По формуле (3.3) получим:
s = 2·4 – 5 – 3 = 0.
Ответ: число степеней свободы фермы s = 0.
Пример 3.2. Определить число степеней свободы системы, предполагая, что все грузы движутся прямолинейно (рис. 3.2).
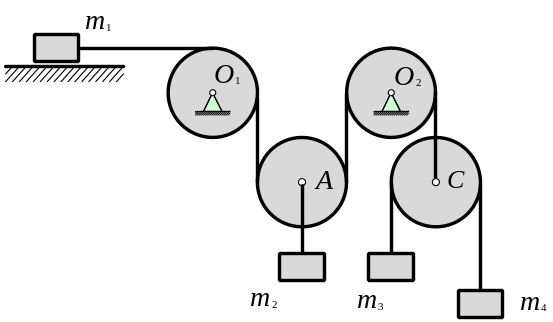
Рис. 3.2
Решение. Закрепим тело с массой m1 , то есть наложим на систему дополнительную – линейную связь, препятствующую смещению этого тела. Тогда диск А с прикрепленной к нему массой m2 сможет перемещаться только вследствие вращения диска с центром О2 .
Наложим на систему вторую дополнительную – моментную связь, препятствующую вращению этого диска. Тогда грузы с массами m1 и m2 будут оставаться неподвижными, а грузы с массами m3 и m4 смогут перемещаться вследствие вращения диска с центром С.
Наложим на систему третью дополнительную связь, препятствующую вращению этого диска. Теперь все четыре груза будут неподвижными. Таким образом, s = 3.
Ответ: число степеней свободы системы s = 3.
Пример 3.3. Определить число степеней свободы системы, состоящей из поступательно движущегося тела А, барабана В и дисков С и D с намотанными на них нитями, если центры последних движутся вертикально (рис. 3.3, а).
Рис. 3.3
Решение. Закрепим тело А, наложив на систему дополнительную линейную связь, препятствующую его смещению. При этом барабан В также будет оставаться неподвижным, а перемещаться смогут только диски С и D.
Наложим на систему вторую дополнительную – моментную связь, препятствующую вращению диска С.
Фактически это означает, что на него наложена связь в виде скользящей заделки, поскольку по условию задачи этот диск может перемещаться только вертикально. При этом центр диска С также будет оставаться неподвижным, а нить между телами В и С – натянутой, и перемещаться сможет только диск D.
Вводя, наконец, третью дополнительную связь, препятствующую вращению диска D , мы получим систему, число степеней свободы которой равно нулю. Таким образом, s = 3. При этом с учетом условий задачи и дополнительно наложенных связей система примет вид, показанный на рис. 3.3, б.
Отметим, что было бы неправильно вместо второй дополнительной моментной связи, препятствующей вращению диска С, ввести линейную связь, которая исключает линейное перемещение его центра, поскольку нить не препятствует вращению этого диска по ходу часовой стрелки.
Аналогичное замечание касается и диска D.
Ответ: число степеней свободы заданной системы равно трем: s = 3.