1.3. Дифференциальные уравнения движения материальной точки

Под законом движения в кинематике понимают алгоритм, позволяющий определить положение движущейся точки в пространстве в любой момент времени.

Различают три способа задания движения: векторный, координатный и естественный. Первый из них представляет собой, главным образом, теоретический интерес, а два последних имеют непосредственное практическое значение.

Дифференциальные уравнения в декартовых координатах. Проектируя основное уравнение динамики (1.1) на оси декартовой прямоугольной системы координат, получим:

(1.2)

Полученная система трех дифференциальных уравнений второго порядка, описывающих движение материальной точки, и называется дифференциальными уравнениями (ДУ) движения материальной точки в декартовых координатах.

Дифференциальные уравнения в естественных координатах. Проектируя основное уравнение динамики (1.1) на оси естественной системы координат, получим:

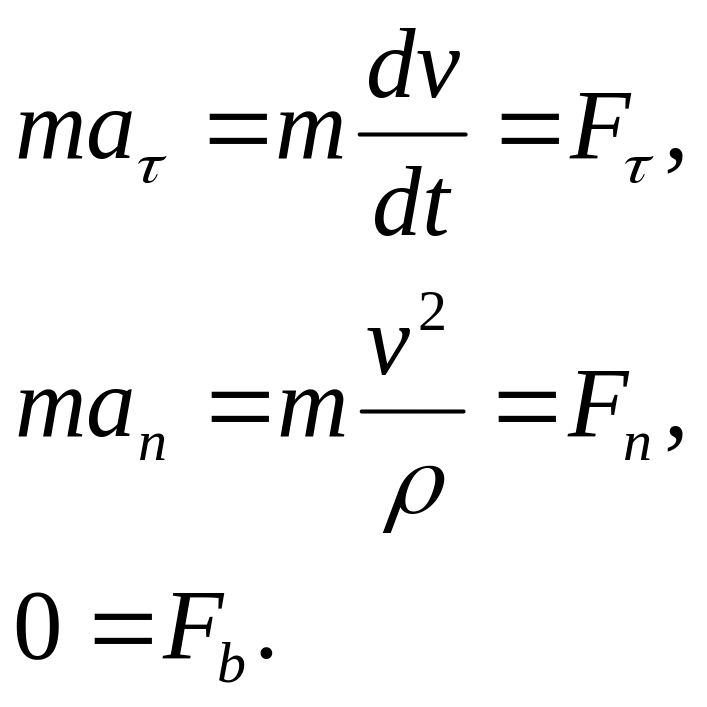
(1.3)

Полученная система дифференциальных уравнений называется дифференциальными уравнениями (ДУ) движения материальной точки в естественных координатах.

Напомним, что вектор ускорения лежит в соприкасающейся плоскости и проекция ускорения на бинормаль – a_b равна нулю.

Глава 2. Динамика материальной точки

2.1. Две задачи динамики

В динамике решают две основные задачи, которые мы и рассмотрим. Методика решения каждой из этих задач зависит от способа задания движения точки.

2.1.1. Первая задача динамики

Задача формулируется следующим образом: найти силу, действующую на точку с массой m, движущуюся по известному закону.

Решение задачи основано на умении находить вектор ускорения a при различных способах задания движения.

· Векторный способ задания движения предполагает, что известна зависимость r = r (t).

Чтобы решить поставленную задачу нужно определить ускорение a = dv/dt = d²r/dt² , а затем с помощью (1.1) – искомую силу F = ma = md²r/dt².

· Координатный способ задания движения предполагает, что известны зависимости:

x = f₁(t), y = f₂(t), z = f₃(t).

Дифференцируя их дважды, найдем проекции вектора ускорения на оси координат:

откуда с помощью (1.2) – проекции искомой силы: F_x , F_y и F_z , по которым легко найти ее модуль и направление:

F = |F| = ,

cos(F,i) = F_x /F, cos(F,j) = F_y /F, cos(F,k) = F_z /F.

Пример 2.1. Найти силу, под действием которой точка с массой m движется по закону:

x = acos(ωt), (а)

y = bsin (ωt).

Решение. Исключив из этих соотношений время t, получим уравнение траектории движущейся точки:

(x/a)² + (y/b)² = 1.

Дифференцируя (а), получим:

Подставляя в (1.2), найдем:

F = |F| = mω²r, cos(F, i) = – x/r , cos(F, j) = – y/r,

______

где r = √ x² + y² (рис. 2.1).

Рис.2.1

Ответ: точка движется в плоскости xOy под действием квазиупругой силы F = – mω²r. ·

· Естественный способ задания движения предполагает, что известна траектория и закон движения точки по траектории: s = f(t) .

Чтобы найти действующую на точку силу нужно вычислить проекцию вектора скорости на направление орта касательной:

v_τ = ds/dt = ,

проекции касательного и нормального ускорений:

a_τ = d²s/dt² = , a_n = v²/ρ ,

а затем из уравнений (1.3) определить проекции вектора силы на эти направления:

F_τ = ma_τ и F_n = ma_n .

После этого легко найти ее модуль и направление:

F = |F| = , cos (F, τ) = F_τ /F, cos (F, n) = F_n /F.

Пример 2.2. Найти силу натяжения нити T и скорость v конического маятника весом P, если нить длиной l образует с вертикалью угол α (рис. 2.2).

Решение. Проектируя основное уравнение динамики для нашей задачи:

ma = P + T

на оси естественной системы координат τ , n и b, получим:

mdv/dt = 0; (а)

mv²/ρ = Tsinα; (б)

0 = Tcosα – P, (в)

где P = mg.

Из (а) следует, что v = const, а из (в) получим:

T = P/cosα.

Подставляя последнее выражение в (б), получим:

mv²/(lsinα) = mg tgα,

откуда найдем скорость конического маятника:

_________

v = √gl sinα tgα .

_________

Ответ: T = P/cosα, v = √gl sinα tgα . ·