12.3 Обобщенные скорости

Скорость i – той точки системы как производная от ее радиус-вектора с учетом зависимости (12.1) будет равна:

v_i = (dr_i /dt) = [(∂r_i /∂q_j) + (∂r_i /∂t)], (12.4)

где – обобщенная скорость. При этом из (12.4) следует, что:

(∂v_i /∂ ) = (∂r_i /∂q_j). (12.5)

Покажем, что справедливо еще одно соотношение:

(∂v_i /∂q_j) = (d/dt) (∂r_i /∂q_j). (12.6)

В самом деле, из выражения (12.4) учитывая, что в нем индекс суммирования является свободным и может быть заменен индексом k, получим:

(∂v_i /∂q_j) = (∂/∂q_j) [(∂r_i /∂q_k) + (∂r_i /∂t)] = [(∂²r_i /∂q_k ∂q_j) + (∂²r_i /∂t∂q_j)].

Но, с другой стороны:

(d/dt) (∂r_i /∂q_j) = [(∂²r_i /∂q_j ∂q_k) + (∂²r_i /∂q_j ∂t)],

откуда и следует (12.6).

12.4 Уравнения Лагранжа II рода

Кинетическая энергия системы:

T = Σ_i (m_iv_i²/2) = (1/2) Σ_i (m_iv_iv_i) (12.7)

с учетом зависимости (12.4) является функцией обобщенных координат, обобщенных скоростей и времени t:

T = T(q₁, q₂,…, q_s, , t).

Частные производные от нее по обобщенным координатам и обобщенным скоростям с учетом (12.7) и (12.5) будут равны:

(∂T/∂q_j) = Σ_i m_iv_i (∂v_i /∂q_j); (12.8)

(∂T/∂ ) = Σ_i m_iv_i (∂v_i /∂ ) = Σ_i m_iv_i (∂r_i /∂q_j).

Найдем полную производную по времени от последнего выражения:

(d/dt)(∂T/∂ ) = Σ_i m_i (dv_i /dt)(∂r_i /∂q_j) + Σ_i m_iv_i (d/dt)(∂r_i /∂q_j). (12.9)

Преобразуем первую сумму в правой части (12.9) с учетом основного уравнения динамики и выражения (12.2):

Σ_i m_i (dv_i /dt)(∂r_i /∂q_j) = Σ_i m_i a_i (∂r_i /∂q_j) = Σ_i (F_i + N_i)(∂r_i /∂q_j) = = Q_j ,

где Q_j – обобщенная сила, соответствующая обобщенной координате q_j . При этом для идеальных связей

= Σ_i (N_i)(∂r_i /∂q_j) = [Σ_i (N_i)(∂r_i /∂q_j)δq_j]/δq_j = (Σ_i N_i δr_i)/δq_j = 0

в силу соотношения (10.1):

ΣN_i δr_i = 0. (10.1′)

Вторая сумма в правой части (12.9) с учетом (12.6) и (12.8) будет равна:

Σ_i m_iv_i (d/dt)(∂r_i /∂q_j) = Σ_i m_iv_i (∂v_i /∂q_j) = (∂T/∂q_j).

Подставляя в (12.9), получим искомые уравнения Лагранжа II рода:

(d/dt)(∂T/∂ ) – (∂T/∂q_j) = Q_j , (j = 1, 2, …, s). (12.10)

Это дифференциальные уравнения второго порядка относительно переменных q₁, q₂,…, q_s.

Интегрируя (12.10) с учетом начальных условий: q_j (0) = q_j⁰ , , получим уравнения движения системы в обобщенных координатах:

q_j = q_j (t), (j = 1, 2, …, s).

12.5 Структура уравнений Лагранжа

Покажем, что кинетическая энергия системы является квадратичной функцией обобщенных скоростей.

Подставляя формулу скорости k-ой точки (12.4):

v_k = (dr_k /dt) = [(∂r_k /∂q_j) + (∂r_k /∂t)], (12.4′)

в выражение кинетической системы:

T = (1/2) Σ_k (m_kv_k)²

получим:

T = (1/2) m_k [ (∂r_k /∂q_i) (∂r_k /∂q_j) +

+ 2 (∂r_k /∂q_i)(∂r_k /∂t) + (∂r_k /∂t)² = T₂ + T₁ + T₀,

где

T₂ = (1/2) A_ij

– квадратичная функция обобщенных скоростей с коэффициентами:

A_ij = A_ij (q₁, q₂,…, q_s, t) = m_k (∂r_k /∂q_i) (∂r_k /∂q_j);

T₁ = B_i

– линейная функция обобщенных скоростей с коэффициентами:

B_i = B_i (q₁, q₂,…, q_s, t) = m_k (∂r_k /∂q_i) (∂r_k /∂t);

T₀ = T₀ (q₁, q₂,…, q_s, t) = (1/2) m_k (∂r_k /∂t)²

– функция нулевой степени относительно обобщенных скоростей.

Для стационарных связей ∂r_k /∂t = 0, поэтому коэффициенты B_i и T₀ равны нулю, а кинетическая энергия системы будет однородной квадратичной функцией обобщенных скоростей или квадратичной формой:

T₂ = (1/2) A_ij ,

при этом коэффициенты A_ij = A_ji зависят только от обобщенных координат, но не от времени.

Именно с таким случаем встречаются студенты второго курса при выполнении своих самостоятельных проектировочных работ по теоретической механике.

Теперь нетрудно доказать, что уравнения Лагранжа являются дифференциальными уравнениями второго порядка.

В самом деле, кинетическую энергию системы в общем случае можно представить в виде:

T = (1/2) A_ij + B_i + T₀ ,

поэтому

∂T/∂ = A_ij + B_i

– будет линейной функцией обобщенных скоростей, а

(d/dt)(∂T/∂ ) =

– дифференциальным оператором второго порядка.

Пример 12.1. Определить ускорение груза A, принимая барабан B за однородный цилиндр и полагая m_A = m_B (рис. 12.2, а).

Решение. Рассматриваемая система имеет одну степень свободы и в качестве обобщенной координаты удобно выбрать угол поворота барабана B или величину линейного смещения груза A как это сделано в нашем примере (рис. 12.2, б).

Для q₁ = s уравнение (12.10) примет вид:

(d/dt)(∂T/∂ ) – (∂T/∂s) = Q_s , (а)

где

T = T^A + T^B = (1/2)m_Av_A² + (1/2)(m_BR²/2)(v_A/R)² = (3/4)mv_A² = (3/4)m ² .

Вычисляем частные производные от кинетической энергии по обобщенным координатам и обобщенным скоростям:

∂Т/∂s = 0;

(б)

∂Т/∂ = (3/2)m .

Для вычисления Q_s сообщим системе возможное перемещение δs = δs_A и подсчитаем работу внешних сил, приложенных к точкам системы на перемещениях точек их приложения:

δA_s = P_A δs_A = mgδs ,

откуда

Q_s = δA_s/δs = mg . (в)

Подставляя (б) и (в) в (а), получим:

(3/2)m = mg,

откуда искомое ускорение груза A будет равно: a_A = = (2/3)g.

Ответ: a_A = (2/3)g. ●

Пример 12.2. Системы, состоящая из однородного диска А радиуса r с намотанной на него нитью и тела В движется под действием собственного веса. Определить обобщенные ускорения и , полагая m_A = m_B = m и пренебрегая трением и весом блока С (рис. 12.3, а).

Решение. Воспользуемся уравнениями (12.10), которые для заданной системы с двумя степени свободы примут вид:

= Q_s ;

(a)

= Q_φ .

Кинетическая энергия системы равна сумме кинетической энергии диска А, участвующего в плоском движении, и кинетической энергии тела В, движущегося поступательно:

Т = Т_А + Т_В = m_Av_A²/2 + J_Aω_A²/2 + m_Bv_B²/2. (б)

Скорость центра диска А можно найти по теореме о скоростях точек плоской фигуры: она складывается из скорости полюса А_Р, в качестве которого удобно взять точку диска, касающуюся вертикального участка нити, и скорости этого центра в его вращении вокруг полюса А_Р:

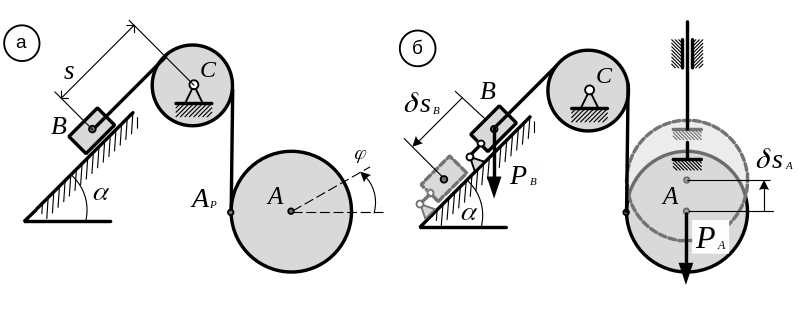Рис. 12.3

v_B = ; v_A = ( + ).

Подставляя в (б) и учитывая, что J_A = (m_Ar²)/2, а ω_A = , получим:

Т = m_A( + )²/2 + m_Ar² /4 + m_B /2.

Вычисляем частные производные от кинетической энергии по обобщенным координатам и обобщенным скоростям:

∂Т/∂s = ∂Т/∂φ = 0;

∂Т/∂ = m_A( + ) + m_B ; (в)

∂Т/∂ = m_A( + )r + m_Ar² /2.

Для определения обобщенных сил Q_s и Q_φ, соответствующих обобщенным координатам q₁ = s и q₂ = φ сообщим системе возможное перемещение δs > 0, δφ = 0.

Фактически это означает, что на систему наложены две дополнительные связи: моментная – на диск А, препятствующая его повороту, и линейная – на тело В, а затем последней связи сообщено возможное перемещение δs_В = δs > 0 (Рис. 12.3, б).

Элементарная работа активных сил, приложенных к точкам системы, на этом перемещении будет равна:

δA_s=g(m_B sinδs_B – m_Aδs_A) = mg(sin – 1)δs,

поскольку δs_B = δs_A = δs, а соответствующая обобщенная сила:

Q_s = δA_s/δs = mg(sin – 1). (г)

Аналогично сообщая системе возможное перемещение δs = 0, δφ > 0, и вычисляя элементарную работу

δA_φ = – mgδs_A,

с учетом соотношения δs_A = rδφ получим:

Q_φ = δA_φ/δφ = – mgr. (д)

Подставляя (в), (г) и (д) в (a), получим:

;

.

Решая полученную систему уравнений, найдем искомые выражения обобщенных ускорений:

(g/4)(3sin – 1);

= – (g/2r)(sin + 1).

Ответ: (g/4)(3sin – 1); = – (g/2r)(sin + 1). ●

Примечания:

1. Приведенные примеры наглядно демонстрируют достоинства полученных Лагранжем уравнений, которые не содержат реакций идеальных связей и позволяют найти ускорения точек системы с одной степенью свободы так же просто, как с помощью теоремы об изменении кинетической энергии системы.

2. Самое главное – эти уравнения позволяют рассматривать системы с любым конечным числом степеней свободы и находить законы их движения.

3. Отметим, что при выполнении контрольных и самостоятельных проектировочных работ на данную тему студенты, как правило, допускают ошибки, связанные не с динамикой, а с кинематическим анализом представленного механизма.