5. Применение пвп для определения опорных реакций рам

При определении опорных реакций рам удобнее пользоваться этим методом в форме принципа возможных скоростей (10.3).

Будем придерживаться следующего плана решения задачи:

1) в соответствии с принципом освобождаемости от связей отбрасываем связь, которая соответствует искомому усилию, и заменяем ее реакцией R_i ;

2) сообщаем точке приложения R_i в полученной системе с одной степенью свободы возможную скорость v_i ;

3) записываем условие равенства нулю мощностей всех активных сил, добавляя к ним неизвестную реакцию R_i :

S( F_i v_i ) = 0; (10.3´)

4) выражаем скорости всех точек системы через скорость какой-либо одной точки;

5) определяем искомую реакцию R_i ;

6) проверяем, если это возможно, правильность решения задачи.

Пример 7.1. Определить горизонтальную составляющую реакции опоры В трехшарнирной рамы (рис. 10.8, а).

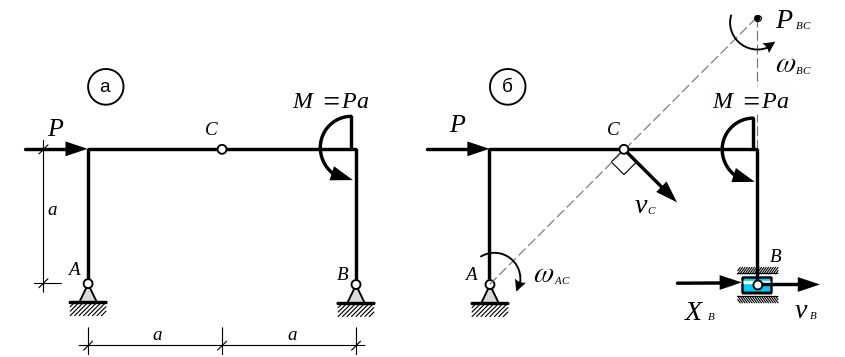
Рис. 10.8

Решение: Отбрасывая горизонтальную связь в шарнире В, получим ползун, к которому приложена неизвестная реакция Х_В (рис. 10.8, б).

Сообщим ему возможную скорость v_B. При этом все точки полученного механизма с одной степенью свободы также получат возможные скорости, а его звенья АС и ВС – угловые скорости ω_АС и ω_ВС соответственно.

Учитывая, что точка А является мгновенным центром скоростей звена АС, определим направление скорости точки С, что позволит построить мгновенный центр скоростей звена ВС – точку Р_ВС.

Поскольку v_С = ω_АСАС = ω_ВССР_ВС , и АС = СР_ВС = а ,то ω_АС = ω_ВС, а так как скорость точки приложения силы – v_Р  Р, то уравнение (5.6) для нашей задачи примет вид:

Pv_P + Mω_ВС + Х_В v_B = 0.

Учитывая, что v_P = ω_АС а = ω_ВС а , а v_B = ω_ВС2а, получим:

(Pa +Pa + Х_В 2a) ω_ВС = 0,

откуда Х_В = – Р.

Чтобы убедиться в правильности решения задачи нужно дополнительно определить Х_A или Y_В , а затем воспользоваться уравнениями ΣХ_i = 0 или ΣM_C^(прав) = 0 соответственно.

Ответ: Х_В = – Р. ●

Глава 11. Принцип даламбера – лагранжа

Этот принцип, как и следует из его названия, представляет собой сочетание двух уже известных нам принципов: принципа Даламбера и принципа возможных перемещений Лагранжа и формулируется следующим образом:

В каждый момент времени сумма работ всех активных сил и сил инерции на любых возможных перемещениях системы, подчиненной идеальным, стационарным и двухсторонним связям, равна нулю:

∑(F_i + Φ_i) δr_i = 0. (11.1)

Для доказательства запишем формулировку принципа Даламбера для системы материальных точек:

F_i + N_i + Φ_i = 0, (i = 1, 2,…, n), (11.2)

где F_i – равнодействующая активных сил, приложенных к i-той точке системы, N_i – равнодействующая реакций связей, приложенных к этой точке, а Φ_i – сила инерции.

Если система подчинена стационарным и двухсторонним связям, то в каждый момент времени будет справедлив принцип возможных перемещений, в соответствии с которым:

∑( F_i + N_i + Φ_i) δr_i = 0,

а поскольку связи системы идеальны, то с учетом (10.1) отсюда и будет следовать (11.1).

Пример 11.1. Определить ускорение груза A, принимая барабан B за однородный цилиндр и полагая m_A = m_B (рис. 11.1, а).

Решение. В соответствии с принципом Даламбера прикладываем к системе активные силы P_A и P_B , и реакцию подшипника N_B (рис.  11.1, б).

Силы инерции поступательно движущегося тела A заменяем равнодействующей

Φ_A = Φ_A = m_A a_A ,

а силы инерции барабана B моментом

M_B ^ин = J_B_B = (m_BR²/2) _B.

Сообщим телу A нашей системы с одной степенью свободы возможное перемещение δs_A , коллинеарное вектору ускорения a_A. При этом барабан B получит возможное угловое перемещение δφ_B .

Запишем уравнение ПВП (11.1), которое для нашей задачи примет вид:

(P_A – Φ_A) δs_A – M_B^ин δφ_B = 0

или

(m_A g – m_A a_A) δs_A – J_B_B δφ_B = 0. (а)

Выразим в последнем соотношении δφ_B и _B соответственно через δs_A и a_A. С этой целью воспользуемся зависимостью:

ω_B = v_A/R,

дифференцируя и интегрируя которую, получим:

_B = a_A/R, δφ_B = δs_A/R. (б)

Подставляя (б) в (а), придем к выражению:

(m_A g – m_A a_A) δs_A – (m_BR²/2) (a_A/R) (δs_A/R) = 0,

откуда, поделив на δs_A ≠ 0, найдем искомое ускорение груза A:

a_A = 2/3 g.

Ответ: a_A = 2/3 g. ●

Примечания:

1. Применение принципа Даламбера – Лагранжа в отличие от непосредственного использования принципа Даламбера позволяет исключить из рассмотрения реакции идеальных связей и тем самым упростить решение. В частности, при определении ускорения в задаче из примера 9.2 на странице 79 – избежать решения системы уравнений и найти ускорение груза A независимо от натяжения нитей T_BA и T_BC .

2. При определении ускорения с помощью принципа Даламбера – Лагранжа рекомендуется придерживаться следующего порядка решения задачи:

1. приложить к телам системы активные силы, реакции связей, не являющихся идеальными, и силы инерции;

2. сообщить одному из тел системы возможное перемещение, совпадающее по направлению с ускорением этого тела;

3. составить уравнение принципа Даламбера – Лагранжа;

4. выразить ускорения и возможные перемещения каждой i-ой точки системы через, соответственно, ускорение и возможное перемещение какой либо одной j-ой точки с учетом зависимостей:

a_i /a_j = v_i /v_j = s_i /s_j = s_i /s_j ;

5. определить искомое ускорение.

3. Уравнение принципа Даламбера – Лагранжа в учебной литературе носит также название общего уравнения динамики.