2. Принцип возможных перемещений и принцип возможных скоростей

Принцип возможных перемещений (ПВП) эквивалентен уравнениям равновесия элементарной статики. Он формулируется следующим образом.

Для равновесия системы, подчиненной идеальным, стационарным и двухсторонним связям, необходимо и достаточно равенства нулю суммы работ всех активных сил на любых возможных перемещениях системы:

ΣF_i δr_i = 0. (10.2)

Принцип можно применять также для систем с неидеальными и односторонними связями. При этом надо включить реакции таких связей в число активных сил и убедиться, что на возможных перемещениях системы они сохраняют свой знак.

Учитывая, что v_i = dr_i /dt , а для стационарных связей действительные перемещения принадлежат к числу возможных, уравнению (10.2) можно придать форму принципа возможных скоростей:

S( F_i v_i ) = 0. (10.3)

Он означает, что для равновесия системы, подчиненной идеальным, стационарным и двухсторонним связям, необходимо и достаточно равенства нулю суммы мощностей всех активных сил на любых возможных перемещениях системы.

С помощью этого принципа можно определять соотношение между силами и моментами, приложенными к подвижной механической системе – механизму, а также находить опорные реакции неподвижных систем.

Чтобы найти зависимость между силами и моментами, приложенными к подвижной механической системе, надо непосредственно применить соотношения (10.2) или (10.3), при этом в первом случае решение сводится к формальным математическим операциям, а во втором – опирается на положения кинематики твердого тела.

Для того чтобы определить опорные реакции неподвижной системы, предварительно надо воспользоваться принципом освобождаемости от связей.

Пример 10.1. В кулисном механизме при качании рычага ОС вокруг шарнира О ползун А, перемещаясь вдоль ОС, приводит в движение стержень АВ, движущийся в направляющих К. Найти зависимость между Q и Р, если ОС = R, ОК = l (рис. 10.2).

Рис. 10.2

Решение. Для нашей системы соотношение (10.2) примет вид:

P δr_A + Q δr_C = 0,

или, в координатной форме:

P_xδx_A + P_yδy_A + Q_xδx_C + Q_yδy_C = 0, (а)

где

P_x = 0, P_y= P, Q_x = Q sinφ, Q_y = – Q cosφ. (б)

Учитывая, что y_A= l·tgφ, x_C= R·cosφ, а y_C = R·sinφ, с помощью обычных правил дифференцирования найдем вариации координат для этих точек системы:

δy_A= (∂y_A/∂φ) δφ = (l/cos²φ) δφ; δx_C = – R·sinφ δφ; δy_C = R·cosφ δφ. (в)

Подставляя (б) и (в) в (а), придем к соотношению:

[(Pl)/(cos²φ) – QR(sin²φ + cos²φ)] δφ = 0,

откуда получим искомую зависимость:

Q = (Pl)/(R cos²φ). ●

Пример 10.2. Определить соотношение между силой F и моментом M, при котором механизм, изображенный на чертеже, находится в равновесии, если ОА = r (рис. 10.3, а).

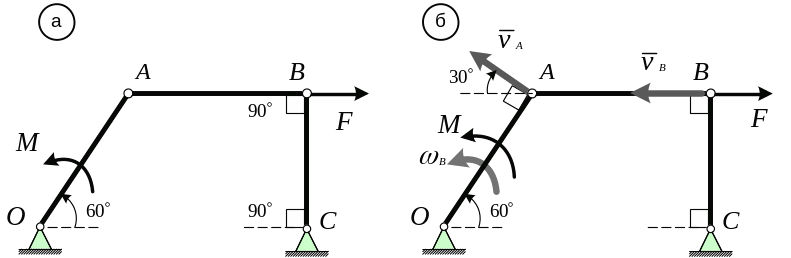
Рис. 10.3

Решение. Воспользуемся для решения задачи соотношением (10.3). С этой целью сообщим звену ОА возможную угловую скорость ω₀ . Поскольку данный механизм имеет одну степень свободы, точки А и В также получат возможные линейные скорости v_A и v_В (рис. 10.3, б).

При этом v_A  ОА и v_A = ω₀·r, а скорость точки В, принадлежащей звену АВ, – v_В  СВ, и ее можно найти с помощью мгновенного центра скоростей или по теореме о проекциях скоростей двух точек плоской фигуры, согласно которой пр_АВv_A = пр_АВv_В, откуда v_В = v_A cos 30 = ω₀ r( /2).

Для нашей задачи нагрузка представлена только парой с моментом M, приложенной к звену ОА и силой F, приложенной в точке В, поэтому соотношение (10.3) примет вид:

M ω₀ + (F · v_В) = 0

или

M ω₀ – F ω₀ r ( /2) = 0,

откуда M = Fr ( /2) .

Ответ: M = Fr ( /2) ●

Примечания:

1. Решение задачи, рассмотренной в примере (10.1) и взятой из сборника задач под редакцией И.В. Мещерского, обычными методами статики приводит к затруднениям, в чем неоднократно убеждались преподаватели кафедры теоретической механики, когда предлагали эту задачу первокурсникам на студенческой олимпиаде.

2. Требование малости перемещений в определении возможных перемещений и в формулировке ПВП для механики твердого тела не является принципиальным.