Глава 8. Потенциальное поле сил

8.1. Основные понятия

В этой главе мы дадим ответы на два вопроса, поставленных в предыдущей главе:

– почему элементарная работа силы обозначается через A, а не через dA?

– в каком случае работа силы не зависит от вида траектории точки ее приложения?

Рассмотрим область , принадлежащую трехмерному эвклидову пространству.

Определение 1. В области  задано скалярное поле, если каждой точке M(x, y, z) этой области поставлено в соответствие число U(x, y, z).

Примерами скалярного поля являются поле температур или поле освещенности.

Определение 2. В области  задано векторное поле, если каждой точке M(x, y, z) этой области поставлен в соответствие вектор F(x, y, z), зависящий от координат этой точки.

Если эта зависимость не меняется со временем, поле называется стационарным. Примером такого поля будет поле скоростей стационарного потока жидкости.

Важным примером векторных полей являются силовые поля. Например – гравитационное или электростатическое.

Определение 3. Стационарное силовое поле F(x, y, z) называется потенциальным, если работа сил этого поля не зависит от вида траектории и определяется начальным и конечным положением точек их приложения.

Силы такого поля называются потенциальными или консервативными.

8.2. Потенциальная энергия системы

Рассмотрим систему материальных точек M_i (x_i , y_i , z_i) в потенциальном силовом поле F(x, y, z), где на каждую точку действует сила F_i (x_i , y_i , z_i).

Примем некоторое положение нашей системы за начальное или иначе нулевое: M_i⁽⁰⁾ (x _i ⁽⁰⁾ , y_i⁽⁰⁾, z_i⁽⁰⁾).

Определение. Потенциальной энергией системы (x, y, z) = (x₁, y₁, z₁, x₂, y₂, z₂, …, x_n, y_n, z_n) называется сумма работ сил потенциального поля, действующих на точки системы при ее перемещении из данного положения в нулевое.

Теорема. Силовое поле F(x, y, z) будет потенциальным, если его можно представить в виде градиента скалярного поля:

F(x, y, z) = – grad  = – [(d/dx)i + [(d/dy)j + [(d/dz)k], (8.1)

где (x, y, z) – потенциальная энергия системы.

Доказательство. Элементарная работа сил поля, действующих на точки системы, с учетом (8.1) будет равна:

A = F_ir_i = – [(∂/∂x_i)dx_i + (∂/∂y_i)dy_i + (∂/∂z_i)dz_i] = – d.

Тогда на конечном перемещении

A₁₂ = A = – d = ₁ – ₂, (8.2)

а это согласно определению 3 означает, что поле F(x, y, z) потенциально. Теорема доказана.

Следствия:

1. Потенциальная энергия системы определяется с точностью до константы.

2. Силы потенциального поля направлены по нормали к эквипотенциальным поверхностям (x, y, z) = const в сторону уменьшения значения потенциальной энергии.

3. Работа сил потенциального поля на замкнутых траекториях равна нулю.

4. Для потенциального поля сил:

A = d A = – d.

Примечание:

Можно доказать, что условия рассмотренной выше теоремы будут не только достаточными, но и необходимыми.

8.3. Примеры потенциальных силовых полей

Вернемся к примерам вычисления работы сил, приведенным в § 7.3.3., и выясним, какие из рассмотренных там полей будут потенциальными.

В соответствии с теоремой и следствиями из предыдущего параграфа для этого достаточно убедиться, в том, что выполняются соотношения (8.1) или (8.2), либо в том, что dA = – dP.

1) Поле силы тяжести. Элементарная работа силы этого поля будет равна:

A = (– mg)dz = – d(mgz) = – d,

то есть поле потенциально. Его потенциальная энергия описывается с точностью до константы функцией:

 = mgz + const,

а эквипотенциальными поверхностями будут плоскости: z = const (рис. 8.1).

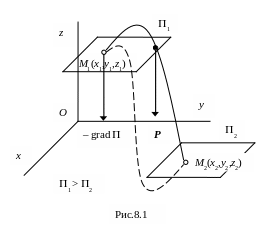
При этом

P = – grad  = – (∂/∂z)k,

A₁₂ = ₁ – ₂.