7.4. Работа сил, приложенных к твердому телу

7.4.1. Работа внутренних сил

Теорема. Работа внутренних сил на любых перемещениях твердого тела равна нулю.

Доказательство приведем для плоского движения тела. Пусть к фиксированным точкам A и B плоской фигуры, движущимся со скоростями v_A и v_B соответственно приложены внутренние силы F₁⁽ⁱ⁾ и F₂⁽ⁱ⁾, которые в силу третьего закона Ньютона равны по модулю и противоположно направлены (рис. 7.5):

F₁⁽ⁱ⁾ = – F₂⁽ⁱ⁾ . (а)

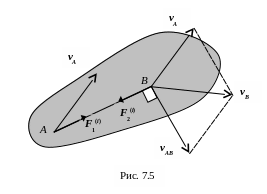
Выбрав в качестве полюса точку A, получим:

v_B = v_A + v_AB , (б)

где v_AB – скорость точки B в ее вращении относительно полюса A, направленная перпендикулярно отрезку AB.

Вычислим элементарную работу сил F₁⁽ⁱ⁾ и F₂⁽ⁱ⁾ :

A(F₁⁽ⁱ⁾, F₂⁽ⁱ⁾) = F₁⁽ⁱ⁾dr_A + F₂⁽ⁱ⁾dr_B = (F₁⁽ⁱ⁾v_A + F₂⁽ⁱ⁾v_B)dt (F₁⁽ⁱ⁾v_A – F₁⁽ⁱ⁾v_B)dt

= (F₁⁽ⁱ⁾v_A – F₁⁽ⁱ⁾v_A – F₁⁽ⁱ⁾v_AB)dt = 0,

поскольку F₁⁽ⁱ⁾v_AB = 0 в силу ортогональности векторов F₁⁽ⁱ⁾ и v_AB .

Теорема доказана.

7.4.2. Работа внешних сил

Рассмотрим, как определяется работа внешних сил, приложенных к твердому телу, при различных случаях его движения.

1) Поступательное движение тела. Элементарная работа сил, приложенных к поступательно движущемуся телу, равна элементарной работе главного вектора внешних сил:

A^(e) = R^(e)dr_c . (7.15)

В самом деле, при поступательном движении твердого тела все его точки имеют геометрически равные скорости, равные скорости центра масс, dr_i = dr_c и поэтому:

A^(e) = F_i^(e) dr_i = (F_i^(e)) dr_c = R^(e)dr_c .

Работа сил на конечном перемещении будет равна интегралу от этого выражения:

A₁₂^(e) = R^(e)dr_c .

2) Вращательное движение тела. Элементарная работа сил, приложенных к телу, вращающемуся вокруг оси Oz, равна произведению главного момента внешних сил относительно оси вращения на элементарный угол поворота тела:

A^(e) = M_o^(e)dφ. (7.16)

Действительно, при повороте тела вокруг оси Oz на угол dφ, точки M_i этого тела с приложенными в них силами F_i получат перемещения dr_i , равные по модулю: dr_i = R_i dφ, где R_i – расстояние от точки M_i до оси вращения, поэтому с учетом (7.9):

A^(e) =  F_i^(e) dr_i =  | F_i^(e) | cos (F_i^(e), dr_i) |dr_i | =  | F_i^(e) | cos (F_i^(e), dr_i) R_i dφ =

=  M_o(F_i^(e)) dφ = M_o^(e)dφ.

Работа сил на конечном перемещении будет равна интегралу от этого выражения:

A₁₂^(e) = M_o^(e)dφ.

3) Плоское движение тела. Элементарная работа сил, приложенных к телу, совершающему плоское движение, определяется выражением:

dA^(e) = R^(e)dr_c + M_c^(e)dφ, (7.17)

где R^(e) – главный вектор внешних сил, приложенных к телу, а M_c^(e) – главный момент внешних сил, приложенных к телу относительно центра C.

В самом деле, произвольную плоскую систему сил, приложенных к телу, можно привести к центру, то есть заменить главным вектором R^(e) и главным моментом M_c^(e). При этом в качестве центра приведения можно выбрать центр масс.

Плоское движение, как известно, можно представить совокупностью двух движений: поступательного движения вместе с полюсом и вращательного движения вокруг этого полюса. Работа главного момента на линейных перемещениях поступательного движения равна нулю и отлична от нуля только на угловых перемещениях, откуда и следует эта формула.