7.3.2. Работа силы на конечном перемещении

Пусть точка приложения силы F перемещается по кривой из первого положения – (1), которое определяется точкой M₁(x₁,y₁,z₁) во второе – (2) c точкой M₂(x₂,y₂,z₂).

Определение. Работа силы на конечном перемещении определяется как криволинейный интеграл второго рода от элементарной работы:

A₁₂(F) = A = (F·dr). (7.11)

При координатном и естественном способах задания движения формула (7.11) примет соответственно вид:

A₁₂(F) = 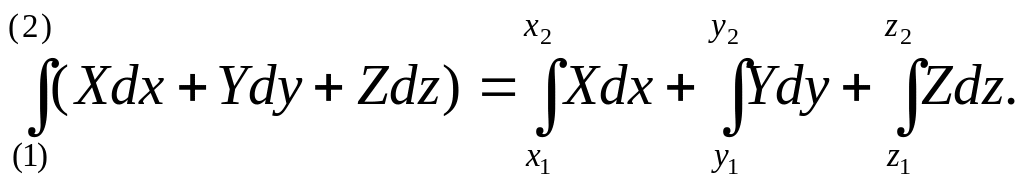(7.11)

A₁₂(F) = | F |cos (F, ) ds = F_·ds. (7.11)

Примечание:

При вычислении работы силы в соответствии со свойствами криволинейного интеграла второго рода:

(F·dr) = – (F·dr);

(F_i)·dr =  (F_i·dr);

(F·dr) = (F·dr) + (F·dr).

7.3.3. Примеры вычисления работы сил

1) Работа постоянной силы на прямолинейном перемещении. Пусть точка приложения силы F перемещается по прямой M₁M₂ на расстояние S и при этом сила остается постоянной по модулю и направлению (рис. 7.2):

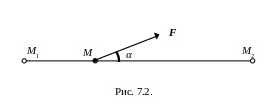
По формуле (7.11)

A₁₂(F) = | F |cos (F, ) ds = F_·ds = (7.12)

Таким образом, работа постоянной силы на прямолинейном перемещении равна произведению модуля силы на модуль перемещения и на косинус угла между направлением силы и перемещением. При этом:

A (F)  0, если 0 < α < π/2,

A (F) = 0, если α = π/2,

A (F) < 0, если π/2 < α < π.

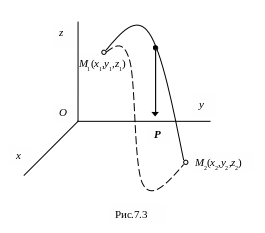
2) Работа силы тяжести. Пусть точка приложения силы тяжести перемещается по кривой из положения M₁ в положение M₂ (рис. 7.3).

В выбранной системе отсчета

P = Xi + Yj + Zk,

где X = Y = 0, а Z = – mg.

Подставляя в (7.11), получим:

A₁₂(P) =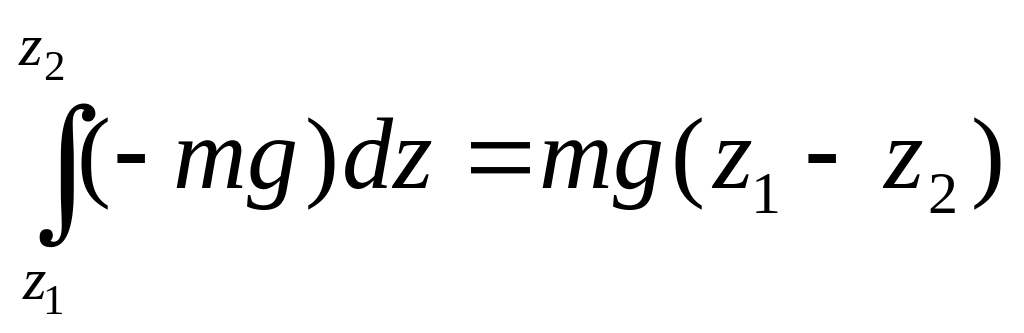 . (7.13)

Таким образом, работа силы тяжести равна произведению веса тела на разность высот начального и конечного положения груза.

При этом работа силы тяжести не зависит от вида траектории точки ее приложения.

То есть, работа силы на траектории, показанной сплошной линией, равна работе той же силы на траектории, показанной пунктиром.

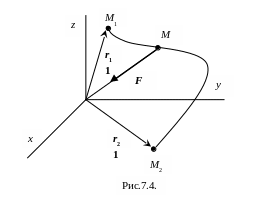
3) Работа упругой силы. Упругой называют силу, которая пропорциональна по модулю и обратна по направлению радиус-вектору, определяющему точку ее приложения (рис. 7.4):

F = – cr .

Такой силой является, например, упругая сила растянутой пружины, рассмотренная в примере 2.4. и в этом случае коэффициент c – это жесткость пружины.

В общем случае такая сила может иметь другую природу и называться квазиупругой или восстанавливающей.

Определим работу упругой силы при перемещении точки ее приложения M по кривой M₁M₂ .

A₁₂(P) = A = (P·dr). (7.11)

По формуле (7.11):

A₁₂(F) = (F·dr) = (–cr)dr = (–c) rdr = (–c/2) d(r²) =

= .

Итак, работа упругой силы равна половине произведения коэффициента жесткости на разность квадратов начального и конечного радиус-вектора. При этом работа упругой силы так же не зависит от вида траектории.

Вернемся к рассмотрению упругой силы растянутой пружины из примера 2.4., выбрав, как и прежде, начало отсчета на конце недеформированной пружины.

Работа упругой силы пружины при ее растяжении из недеформированного состояния будет равна:

A₁₂(F) = (– cx)dx = – (cx²)/2 = – (F·x)/2 . (7.14)

Последнее выражение означает, что работа упругой силы равна половине произведения максимального значения силы на величину соответствующего ей удлинения пружины.