7.2. Кинетическая энергия твердого тела

Определим кинетическую энергию твердого тела при различных видах его движения.

Поступательное движение. При поступательном движении все точки ТТ имеют геометрически равные скорости, равные скорости центра масс. Поэтому непосредственно по формуле (7.1) получим:

T = (1/2)åm_iv_i² = (1/2)Mv_c² . (7.5)

Вращательное движение. При вращении тела вокруг оси Oz точки M_i, удаленные от нее на расстояние R_i , имеют скорость v_i =  R_i , поэтому по формуле (7.1) с учетом (4.6):

T = (1/2)åm_iv_i² = (1/2)å(m_i R_i²) ² = (1/2)J_z², (7.6)

где J_z – момент инерции относительно оси вращения.

Плоское движение тела. Такое движение представляют суммой двух – поступательного движения вместе с произвольно выбранным полюсом и вращения вокруг этого полюса.

Если в качестве последнего выбрать центр масс, можно воспользоваться формулой (7.2) по которой с учетом (7.5) и (7.6) получим:

T = (1/2)Mv_c² + (1/2)J_c² , (7.7)

где J_c – момент инерции относительно центра масс.

Пример 7.1. Определить кинетическую энергию колеса с массой M, которое движется без проскальзывания со скоростью v_c , принимая его за однородный диск (рис. 7.1).

Решение. По условию задачи колесо участвует в плоском движении, поэтому, подставляя в формулу (7.7)  = (v_c / R) и с учетом (4.18): J_c = (MR²/2), получим:

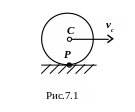
T = (1/2)Mv_c² + (1/2)(MR²/2)(v_c/R)² = (3/4)Mv_c². (7.8)

В дальнейшем можно пользоваться готовой формулой (7.8), не выводя каждый раз ее заново.

Приведем другой вывод формулы (7.8).

Как известно, используя понятие мгновенного центра скоростей (МЦС), можно в каждый момент времени свести плоское движение к вращательному.

В нашем примере МЦС колеса будет точка P, где оно контактирует с неподвижной поверхностью.

Момент инерции диска относительно этой точки найдем с помощью формулы (4.10):

J_p = J_c + M R² = MR²/2 + MR² = (3/2) MR².

Воспользовавшись формулой (7.6) для кинетической энергии вращающегося тела, получим тот же результат:

T = (1/2)J_p² = (3/4)Mv_c².

Ответ: T = (3/4)Mv_c². 

Примечания:

1. Следует обратить внимание, что решение задачи не зависит от радиуса колеса.

2. Кинетическая энергия колеса за счет поступательного движения вдвое больше кинетической энергии, вызванной его вращением.

3. Кинетическая энергия вычисляется для определенного момента времени, поэтому формула (7.8) справедлива для диска, движущегося без проскальзывания по криволинейной поверхности, а также для диска, вращающегося вокруг неподвижной оси, проходящей через центр P и перпендикулярной к плоскости чертежа.

7.3. Работа силы

7.3.1. Элементарная работа силы и ее мощность

Рассмотрим отрезок траектории точки M, в которой приложена сила F.

Определение 1. Элементарная работа силы равна скалярному произведению вектора силы F и вектора элементарного перемещения точки ее приложения dr :

A = (F·dr). (7.9)

Представив F и dr в виде:

F = Xi + Yj + Zk,

dr = dxi + dyj +dzk,

получим аналитическое выражение элементарной работы силы, соответствующее не векторному, а координатному способу задания движения точки приложения силы:

A = Xdx + Ydy + Zdz. (7.9)

Наконец, если известен естественный способ задания движения точки M и дан закон изменения ее дуговой координаты s = f(t) , то формулу (7.9) можно записать в виде:

A = | F |·| dr |·cos (F, dr) = F_·ds, (7.9)

где F_ – проекция силы F на направление орта касательной .

Формулу (7.9) можно представить в следующем виде:

A = (F·dr) = (F·dr)(dt/dt) = (F·dt)(dr/dt) = (F·v)·dt = N·dt,

где

N = (F·v) = (A/dt) (7.10)

– мощность силы.

Таким образом, можно дать следующее определение.

Определение 2. Мощность силы равна скалярному произведению вектора силы и вектора скорости точки ее приложения.

Примечание:

1. В определении 1 речь идет не о материальной, а о геометрической точке M , и не утверждается, что точка M движется под действием этой силы.

2. Из формулы (7.10) следует, что мощность силы равна работе, совершаемой этой силой в единицу времени.

3. Как видно из (7.9) и (7.10) работы силы измеряется в Джоулях, а мощность – в Ваттах:

[A] = [F] [s] = Н·м = Дж,

[N] = [F] [v] = Н·м·c^–1 = Дж/с = Вт.

4. Наглядным примером, поясняющим формулу N = (F·v) будет следующий: автомобиль «Лада» и трактор «Беларусь» имеют приблизительно одинаковую мощность, но совершенно разный внешний вид, потому что выполняют различные функции.

В первом случае – у автомобиля в этой формуле больше второй сомножитель – скорость, а во втором – первый – сила.

5. Причину, по которой элементарную работу силы обозначают не dA, а A мы объясним в следующей главе.