6.2. Теорема для точки

Теорема. Производная от кинетического момента точки относительно центра (оси) равна сумме моментов всех сил, действующих на точку относительно этого центра (оси):

(d/dt) (r  mv) = M_o(F_i), (6.3)

(dk_x/dt) = M_x(F_i), (dk_y/dt) = M_y(F_i), (dk_z/dt) = M_z(F_i). (6.4)

Доказательство. Основное уравнение динамики (1.1):

ma = F, (1.1)

умножим слева на радиус-вектор r и воспользуемся подстановкой a = dv/dt:

r  (d/dt)(mv) = r  F. (6.5)

Учитывая, что

(d/dt) (r  mv) = (dr/dt)  mv + r  (d/dt)(mv) = v  mv + r  (d/dt)(mv) =

= r  (d/dt)(mv) ,

поскольку (v  mv) = 0, а (r  F) = M_o(F), перепишем соотношение (6.5) в виде:

(d/dt) (r  mv) = M_o(F),

откуда и следует соотношение (6.3). Проектируя его на оси координат, получим (6.4).

6.3. Теорема для системы

Запишем соотношение (6.3) для i-ой точки системы:

(d/dt) (r_i  m_iv_i) = (r_i  F_i^(e)) + (r_i  F_i⁽ⁱ⁾).

Просуммировав по всем точкам системы, получим:

(d/dt)  (r_i  m_iv_i) =  (r_i  F_i^(e)) +  (r_i  F_i⁽ⁱ⁾),

откуда следует искомое соотношение:

dK_o/dt = M_o^(e), (6.6)

где M_o^(e) =  (r_i  F_i^(e)) – главный вектор внешних сил.

Проектируя на оси координат, получим:

dK_x/dt = M_x^(e), dK_y/dt = M_y^(e) , dK_z/dt = M_z^(e). (6.7)

Итак, справедлива теорема:

Теорема. Производная от кинетического момента системы относительно центра (оси) равна главному моменту внешних сил относительно этого центра (оси).

Следствие. Из формул (6.6) и (6.7) следует:

1. Если M_o^(e) = 0, то K_o = const.

2. Если M_x^(e) = 0, то K_x = const.

Таким образом, если главный момент внешних сил относительно некоторого центра (оси) равен нулю, то кинетический момент системы относительно этого центра (оси) остается постоянным.

6.4. Дифференциальное уравнение вращения твердого тела

Кинетический момент твердого тела. Пусть твердое тело вращается вокруг оси Oz c угловой скоростью  против хода часовой стрелки.

При этом вектор  направлен вверх, а его проекция на ось Oz положительна: _z = пр_z  0.

Точка M_i этого тела, удаленная на расстояние R_i от оси вращения будет иметь линейную скорость v_i = R_i , а проекция вектора скорости на направление касательной к траектории будет положительной: v_i = пр_v_i  0.

Вычислим кинетический момент вращающегося тела, воспользовавшись формулами (6.2) и (4.6):

K_z = mom_z(m_iv_i) = (m_i v_i R_i) = (m_i _z R_i ²) = (m_i R_i ²) _z = J_z _z .

Итак, кинетический момент тела, вращающегося вокруг оси Oz, равен произведению момента инерции относительно оси вращения на проекцию вектора угловой скорости на эту ось:

K_z = J_z _z . (6.8)

Дифференциальное уравнение вращения ТТ. Подставляя формулу (6.8) в

последнее из соотношений (6.7):

dK_z/dt = M_z^(e), (6.7)

получим искомое ДУ вращения ТТ вокруг этой оси:

J_z(d_z/dt) = J_z _z = M_z^(e). (6.9)

Примечания:

1. Мы рассмотрели две первые теоремы из общих теорем динамики. Приведем для сравнения основные зависимости из этих теорем:

2. Теорема об изменении количества движения системы		Теорема об изменении кинетического момента системы
   Qx = M(dxc/dt)	((1)	Kz = Jz(dj/dt)	(4)
   (dQx/dt) = Rx(e)	((2)	(dKz/dt) = Mz(e)	(5)
   Macx = Rx(e)	((3)	Jzez = Mz(e)	(6)

   Математически соотношения (1)-(3) и (4)-(6) для ТТ эквивалентны, то есть закон движения центра масс системы вдоль оси Ox под действием R_x^(e) аналогичен вращению ТТ вокруг оси Oz под действием M_z^(e).

3. Если тело, вращающееся вокруг оси Oz, не является абсолютно твердым и может изменять свою конфигурацию и момент инерции относительно этой оси, системы не будут эквивалентными.

В самом деле, при R_x^(e) = 0 из (2) и (3) следует, что , а из (5) и (6) при M_z^(e) = 0 следует только то, что K_z0 = K_zt , откуда:

J_z0_z0 = J_zt_zt . (6.10)

Последнее соотношение объясняет поведение танцоров и спортсменов при выполнении пируэта, прыжка в воду или сальто-мортале: группируясь, они уменьшают свой момент инерции, что вызывает увеличение угловой скорости вращения и позволяет сделать максимальное число оборотов. Разгруппировавшись на заключительном этапе и уменьшив, тем самым угловую скорость вращения, они создают благоприятные условия для приземления или вхождения в воду.

4. Теорема об изменении кинетического момента системы дает ответы на такие вопросы как: почему у вертолета Ми-8 помимо основного несущего винта, расположенного над кабиной, на хвосте находится еще один винт, вращающийся в вертикальной плоскости, и почему такого винта нет у вертолета Ка-32? Или, почему при падении на землю кошка, как правило, опускается на лапы, а не на спину?

5. Отметим, что в общем случае в §6.4 K_x и K_y отличны от нуля и непостоянны даже при равномерном вращении тела. Последствия этого мы рассмотрим в главе 9.

Общий случай вычисления кинетического момента тела относительно произвольной неподвижной оси приведен в следующем параграфе.

Пример 6.1. Определить ускорение груза A, принимая барабан B за однородный цилиндр и полагая m_A = m_B (рис. 6.2, а).

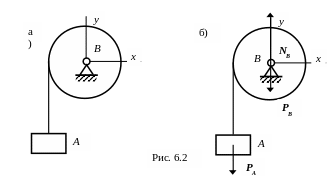
Решение. Система состоит из двух тел: поступательно движущегося груза A и вращающегося барабана B .

Кинетический момент системы относительно оси Oz , перпендикулярной плоскости чертежа и совпадающей с осью вращения барабана будет складываться из кинетических моментов этих двух тел:

K_z = K_z^A + K_z^B = m_Av_AR + J_z_z, (а)

где R – радиус барабана, v_A – скорость тела A, J_z – момент инерции барабана, _z – его угловая скорость.

Подставляя в (а) J_z = (m_BR²/2), _z = v_A/R и полагая m_A = m_B = m, получим:

K_z = m_Av_AR + (m_BR²/2)(v_A/R) = (3/2) mv_AR . (б)

Внешними силами, действующими на систему, будут P_A – вес тела A , P_B – вес тела B и N_B – реакция подшипника барабана B , при этом момент двух последних относительно оси Oz равен нулю (рис. 6.2, б), поэтому

M_z^(e) = P_AR = mgR . (в)

Подставляя (б) и (в) в теорему об изменении кинетического момента системы

(dK_z/dt) = M_z^(e), (6.7)

получим: a_A = (2/3) g.

Ответ: a_A = (2/3) g. 

Примечание:

В дальнейшем мы неоднократно будем возвращаться к рассмотренному примеру, решая для сравнения эту задачу другими методами.