5.4. Теорема о движении центра масс
Подставляя формулу (5.3) в (5.6), получим:
dQ/dt = d(Mvc)/dt = Mac = R(e),
где ac – ускорение центра масс системы.
Полученное соотношение:
Mac = M (dvc /dt) = R(e) (5.9)
по форме и с точки зрения математики не отличается от основного уравнения динамики для материальной точки (1.1):
ma = F, (1.1)
откуда следует, что и законы движения этих двух объектов будут одинаковы, поэтому справедлива следующая теорема.
Теорема. Центр масс механической системы движется как материальная точка с массой, равной массе всей системы, на которую действует главный вектор внешних сил.
Проектируя (5.9) на оси координат, получим:
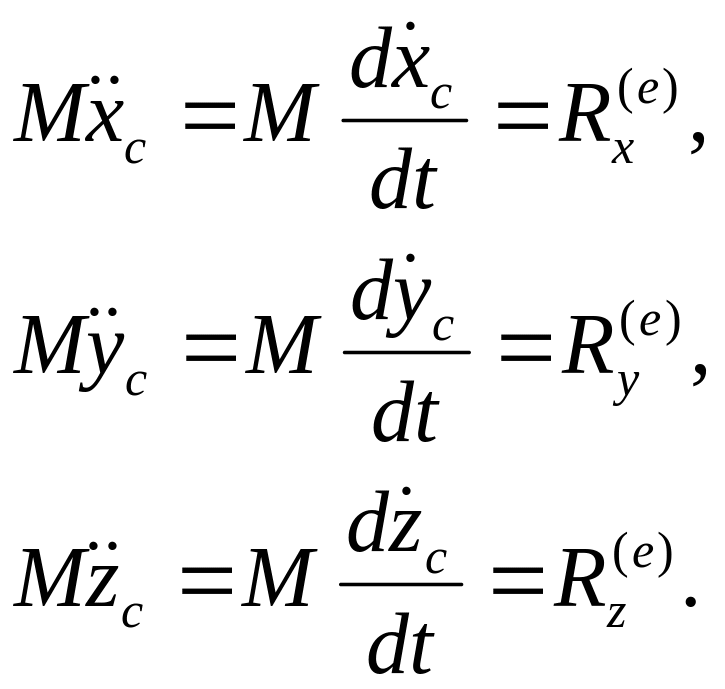
(5.10)
Следствие. Из формул (5.9) и (5.10) следует:
Внутренние силы не влияют на движение центра масс системы.
Если R(e) = 0, то dvc /dt = 0, откуда
vc = vc0 = const,
то есть центр масс движется равномерно и прямолинейно. В частности, если vc0 = 0, то drc /dt = 0, откуда
rc = rc0 = const,
то есть центр масс находится в состоянии покоя.
Таким образом, если главный вектор внешних сил системы равен нулю, то центр масс системы движется прямолинейно и равномерно или находится в состоянии покоя.
Если Rx(e) = 0, то vcx =
=
const, то есть вдоль
соответствующей оси центр масс системы
движется прямолинейно и равномерно. В
частности, если
=
0, то dxc
/dt = 0, откуда
xc = xc0 = const,
то есть координаты центра масс системы вдоль соответствующей оси остаются неизменными.
Итак, если проекция главного вектора внешних сил системы на какую-либо ось равна нулю, то вдоль этой оси центр масс системы движется прямолинейно и равномерно или находится в состоянии покоя.
Пусть, например, ракета с массой корпуса M и массой горючего m находится в состоянии относительного покоя за пределами солнечной системы.
После запуска двигателя корпус ракеты улетает в одну, а сгоревшее топливо – в противоположную сторону на миллионы километров от точки старта, но центр масс системы остается в первоначальном положении в состоянии покоя.
Пример 5.1. По горизонтальной платформе, движущейся со скоростью v0, перемещается тележка с относительной скоростью u0. Найти скорость платформы при торможении тележки, если их массы равны M и m соответственно.
Решение. На систему, состоящую из платформы весом P = Mg и тележки весом p = mg, помимо этих двух сил действует реакция дорожного полотна N, приложенная к основанию платформы (рис. 5.1).
Главный вектор внешних сил системы: R = P + p + N перпендикулярен оси Ox, поэтому Rx(e) = 0 и справедливо следствие из теоремы об изменении количества движения системы (5.7):
dQx/dt = Rx(e) (5.7)
в соответствии с которым
Qx0 = Qxt . (а)
В начальный момент времени абсолютная скорость тележки складывается из переносной, равной скорости платформы, и относительной – u0 , поэтому при t = 0 количество движения системы равно:
Qx0 = Mv0 + m(v0 + u0). (б)
В момент времени t , соответствующий окончанию торможения тележки, количество движения системы равно:
Qxt = (M + m)v, (в)
где v – искомая скорость платформы.
Приравнивая (б) и (в), получим:
v = [Mv0 + m(v0 + u0)]/(M + m) = v0 + mu0/(M + m).
Ответ: v = v0 + mu0/(M + m).
Примечания:
То обстоятельство, что внутренние силы не влияют на движение центра масс, не означает, что они не могут вызвать появление внешних сил. Примером служит работа двигателя внутреннего сгорания автомобиля, который вызывает появление внешних движущих сил, – ими являются силы трения с дорожным покрытием, приложенные к его ведущим колесам.
В физике импульсом точки называется произведение массы точки на ее скорость, то есть то, что в ТМ называется количеством движения, а интегральная форма этой теоремы, то есть формулы (5.5) и (5.8) носит название теоремы импульсов.
Теорема об изменении количества движении системы основана на применении первой подстановки a = dv/dt.
Теорема об изменении количества движении системы позволяет:
– найти первый интеграл, то есть зависимость v = v(t),
– описать движение центра масс системы.
Для описания движения системы вокруг центра масс необходимо рассмотрение видоизмененной формы этой теоремы.