5.4 Дискретизация сигнала, при условии его восстановления методом интерполяции

При этом методе полученные точки просто соединяются между собой отрезками прямых линий. Очевидно, что в этом случае плавные участки, близкие к прямым линиям, восстанавливаются с малыми погрешностями, а максимальная погрешность восстановления получается на участках с максимальной кривизной (рис. ).

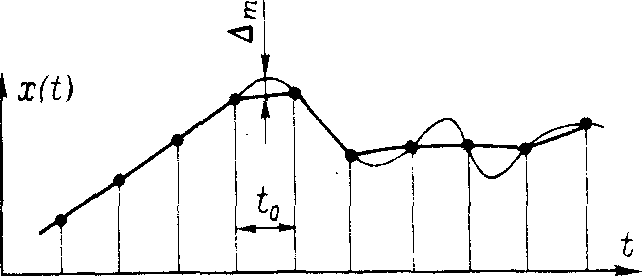
Известно, что любую кривую x(t) на некотором участке можно разложить по степеням t, т. е. описать многочленом. В простейшем случае, используя лишь первые члены разложения, участок кривой между отсчетами можно представить в виде параболы, тогда погрешность линейной интерполяции будет представлять собой разность между этой параболой и ее хордой, соединяющей смежные отсчеты. Как известно, парабола имеет наибольшее отклонение от хорды в середине интервала интерполяции t₀ с абсолютным значением (_m на рис.)

где - значение второй производной процесса х(t) т. е. оценка его кривизны. Отсюда максимальное значение погрешности восстановления наблюдается на участках кривой с наибольшей кривизной (в области максимумов и минимумов процесса предст. на рис.).

Если нас интересует не абсолютная погрешность _m, а ее приведенное значение , где x_k — предел измерений, то можно определить максимальный допустимый период дискретизации t_ц при котором погрешность восстановления не будет превышать _m:

Так как любую сложную кривую можно разложить на ряд гармонических составляющих, то определим необходимый период дискретизации для синусоидального процесса. При x(t)=x_ksint оценка текущей кривизны , а ее максимальное значение . Отсюда необходимый период дискретизации для синусоидального процесса

(3)

Соотношение (3) воспринимается более наглядно, если его помощью вычислить число точек п, приходящихся на каждый период Т синусоидального процесса:

(4)

Это соотношение дает:

m	0,1	1	10	20
n	70	22	7	5

Таким образом, для восстановления синусоидального процесса с максимальной погрешностью 1 % при равномерной дискретизации необходимо иметь 22 отсчета на период процесса, но для представления с погрешностью 0,1% нужно не менее 70 отсчетов на каждый период, а для _m=20% достаточно пяти отсчетов на период.

Исходя из соотношения (4), можно подсчитать минимальный период или максимальную частоту процесса, который может быть зарегистрирован с заданной максимальной погрешностью _m. Данные о максимальных погрешностях при использовании некоторых приёмов и средств приведены в табл. и свидетельствуют о том, что без использования специальных средств могут быть зарегистрированы лишь очень медленные процессы (с периодом 0,2—2 с).

Метод регистрации	t0 с	Период или частота процесса при m , % равной
		0,1	1	10
Запись в журнал с показывающего прибора	6	7 мин.	2,2 мин.	42 с
Цифропечать	0,5	35 с	11 с	3,5 с
Перфоратор	0,027	1,9 с	0,6 с	0,2 с
АЦП с компьтером (условно)	30 10-6	500 Гц	1,5 кГц	5 кГц

Выражая _m из выражения (3) или (4) получаем

(5)

т. е. динамическая погрешность восстановления _m возрастает е квадратом частоты восстанавливаемого процесса.

На практике чаще всего приходится измерять существенно несинусоидальные процессы, содержащие гармонические составляющие или высокочастотные составляющие шумов, помех или наводок. В этих случаях динамическая погрешность восстановления процесса по дискретным отсчетам резко возрастает, о чем исследователь должен всегда помнить.

Рассмотрим это свойство погрешности восстановления на конкретном примере. Так, в табл. указано, что при использовании АЦП с периодом дискретизации t_ц=30 мкс исследуемый процесс с частотой f₁=500 Гц восстанавливается с _m10,1%. Действительно, рассчитывая _m1 по формуле (5), получаем

что часто можно считать достаточно высокой точностью восстановления. Однако если в кривой этого процесса содержится дополнительно еще 10-я гармоника с частотой f₁₀=5000 Гц и амплитудой в 0,1 основной волны, она будет восстанавливаться с относительной погрешностью _m10 , в 100 раз большей, чем _m1, т. е. равной 10%. Правда, так как амплитуда этой гармоники в 10 раз меньше амплитуды основной волны, то приведенное значение этой погрешности составит лишь _m10=1% • Тем не менее результирующая погрешность восстановления всего процесса будет в 10 раз (!) больше, чем погрешность восстановления _m1=0,1% процесса, не содержащего этой высокочастотной составляющей.

Погрешность восстановления для основной волны и ее гармоник является систематической (она всегда отрицательна, см. рис. и приводит к уменьшению восстанавливаемой амплитуды кривой), однако если высокочастотная составляющая вызвана шумом или другими помехами и не синхронна с основной волной, то и погрешность восстановления оказывается случайной и наблюдается в виде случайного разброса отсчетов.

При ручной регистрации наблюдений подобный разброс данных будет сразу замечен экспериментатором и он примет соответствующее решение о ходе эксперимента. Рассмотренное явление особенно опасно при автоматическом вводе данных в компьютер и подчеркивает крайнюю важность метрологического анализа динамических погрешностей в этом случае.

Однако в связи с постоянным увеличением быстродействия компьютеров этот способ дискретизации и восстановления становится очень привлекательным.