10.2 Оптимизация параметров измерительной системы второго порядка из условия минимума длительности переходного процесса.

Одним из важных критериев динамического качества является длительность переходного процесса, определяемая как время, начиная с которого кривая переходного процесса не выходит за границы допустимой динамической погрешности.

Обозначим относительное значение допустимой погрешности через

где _доп – абсолютное значение допустимой погрешности.

При расчетах обычно допускают  = 0,05:-0,1. В области 0 <  < 1 существует оптимальное значение , при котором длительность переходного процесса при выбранном значении ₀ будет наименьшей.

Представим уравнение (25) в безразмерной форме:

(32)

График, построенный по уравнению (32) для трех близких значений , показывает, что минимум безразмерной длительности переходного процесса будет при таком значении =₁, при котором максимум функции (32) после первого перехода через установившееся значения совпадает с верхней границей допустимой динамической ошибки 1+ (кривая 1). Этой кривой соответствует длительность процесса ₁, при которой кривая 1 входит в зону допуска в точке А.

Допустим , что ₂ > ₁ . Тогда период колебаний увеличится и переходный процесс будет описываться кривой 2 , расположенной правее кривой 1 и входящей в зону 1  в точке В, для которой ₂>₁. Если же ₃<₁ (кривая 3), то период колебаний уменьшится, но увеличится величина перехода через установившееся значение, из-за чего максимальное отклонение кривой 3 выйдет за пределы верхней границы допуска +.

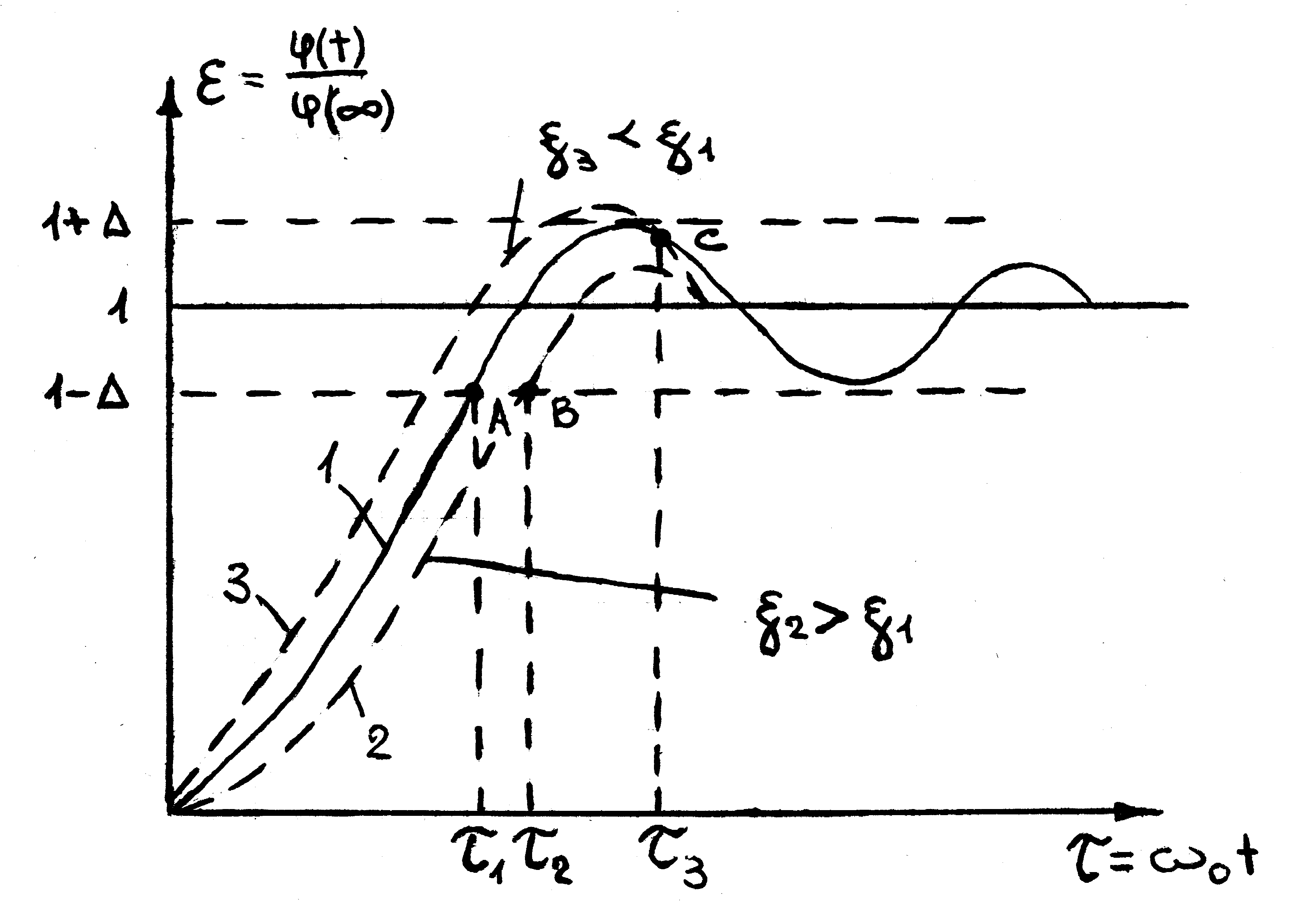
Рис К расчёту оптимальной степени успокоения по критерию минимума длительности переходного процесса

Длительность ₃ процесса будет определяться вторым пересечением кривой 3 с верхней границей зоны допусков в точке С (т.е в зону допуска кривая войдет в конце первого полупериода). Следовательно: ₃>₁.

Таким образом, задача отыскания оптимального значения  сводится к определению такого его значения, при котором первый максимум функции равен 1+. Выражение для оптимального значения  можно найти, приравнивая в формуле (28) =.:

откуда оптимальная степень успокоения:

(33)

Из последней формулы следует, что величина _опт зависит от величины допуска .

Подставляя (33) в (32) и приравнивая  =1- получим уравнение, однозначно определяющее минимальную безразмерную длительность переходного процесса:

,

это уравнение не имеет явного решения относительно _nn , но может быть решено численно. Его численные решения, т.е. зависимость  (_опт, _пп) приведена в таблице:

	0	 0,025	 0,05	 0,1	 0,25
опт	1,0	0,76	0,69	0,59	0,404
пп		2,83	2,6	2,32	1,95

Действительная длительность процесса равна найденному из таблицы значению безразмерной длительности _пп деленному на собственную частоту недемпфированных колебаний:

(34)

Из формулы (34) следует, что длительность переходного процесса теоретически можно неограниченно уменьшать путем увеличения ₀ , однако на практике возможности увеличения ₀ ограничены. Увеличение в случае с маятниковым акселерометром возможно за счет увеличения С и уменьшения J. Если выбран тип чувствительного элемента и определены его размеры, исходя из получения максимального вращающего момента М_max , превышающего в нужное число раз вредные моменты, то при заданном максимальном угле _max поворота подвижной системы, жесткость С определяется из условия равновесия системы в статическом режиме . Что касается момента инерции J, то он складывается из двух составляющих:

J=J_чэ + J_пр ,

где J_чэ – момент инерции подвижной части чувствительного элемента; J_пр –приведенный момент инерции масс подсоединенных к подвижной части, т.е. передаточного механизма, стрелки якоря и т. д.

При выбранном типе и размерах чувствительного элемента величины J_чэ и М_max оказываются взаимосвязанными. Уменьшение J_чэ приведет к уменьшению M_max.. Остается возможность уменьшения J_пр за счет уменьшения масс механизмов подсоединенных к подвижной части. Но здесь также существует предел. Таким образом, в каждой конструкции существует практический максимум собственной частоты

,

следовательно, наименьшая практически достижимая длительность переходного процесса

.

После того как выбраны С, J, ₀ и _опт нетрудно найти оптимальный коэффициент демпфирования: