3.3. Простейшие задачи аналитической геометрии

Как известно из школьной математики метод координат даёт возможность установить соответствие между некоторыми геометрическими объектами и уравнениями. В школе рассматривалась прямоугольная система координат на плоскости (Оху) и говорилось об уравнении прямой, об уравнении параболы и графике функции у = 1 / х и т.д. Сейчас, используя координатный метод и элементы векторной алгебры, мы будем изучать геометрические объекты с более общих позиций. Прежде рассмотрим простейшие задачи аналитической геометрии.

Расстояние между двумя точками

Требуется найти расстояние между двумя точками А(х₁,у₁,z₁) и В(х₂,у₂,z₂) в пространстве Охуz.

Решение. Искомое расстояние d равно длине вектора AB (x₂–x₁,y₂–y₁,z₂–z₁), т.е.

d = | AB | = . (3.18)

Деление отрезка в данном отношении

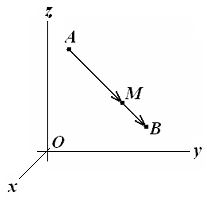Требуется разделить отрезок АВ, соединяющий точки А(х₁,у₁,z₁) и В(х₂,у₂,z₂) в заданном отношении λ>0, т.е. найти координаты точки М (х,у,z) отрезка АВ такой, что АМ/МВ = λ (см. рис. 3.10).

Решение. Введём в рассмотрение векторы АМ и МВ . Точка М делит отрезок АВ в отношении λ если АМ = = λ МВ. Но АМ = (х – х₁, у – у₁, z – z₁) и МВ = (х₂ – х , у₂ – у, z₂ - z) , поэтому

(х – х₁) = λ(х₂ – х), (y – y₁) = λ(y₂ – y) и (z – z₁) = λ(z₂ – z) Рис. 3.10.

или , . . (3.19)

Формулы (3.19) называются формулами деления отрезка в данном отношении. В частности, при λ = 1, т.е. если АМ = МВ, то они примут вид

, , .

В этом случае точка М (х, у, z) является серединой отрезка АВ.

Замечание. Если λ < 0, то точка М лежит вне отрезка АВ – говоря, что точка М делит отрезок АВ внешним образом.

3.4. Аналитическая геометрия в пространстве

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

F(x, y, z) = 0.

Это уравнение называется уравнением линии в пространстве.

Прежде всего, рассмотрим геометрическое место, точек определяемое уравнениями первой степени. Таковыми являются уравнения плоскости и прямой линии в пространстве.

3.4.1. Уравнение плоскости в пространстве

Уравнение плоскости, проходящей через данную точку

перпендикулярно данному вектору

Пусть в пространстве Охyz плоскость π задана точкой М₀(х₀,у₀,z₀) и вектором (А,В,С) , перпендикулярным этой плоскости (рис. 3.11). Найти уравнение плоскости π .

Возьмём на этой плоскости произвольную точку М(х,у,z) и образуем вектор

= (х – х₀, y – y₀, z – z₀).

При любом расположении точки М на плоскости π векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: ∙ = 0, т.е.

. (3.20)

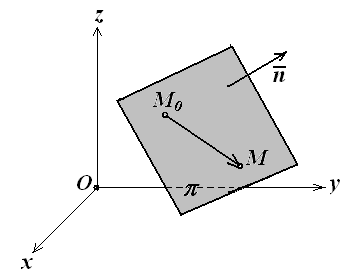
Рис. 3.11.

Уравнение (3.20) называется уравнением плоскости, проходящей через точку М₀(х₀,у₀,z₀) перпендикулярно вектору = (А,В,С).

Оно первой степени относительно текущих координат х, у и z. Вектор = (А,В,С) называется нормальным вектором плоскости.

Придавая коэффициентам А,В, и С уравнения (3.20) различные значения, можно получить уравнение любой плоскости, проходящей через точку М₀ . Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (3.20) – уравнением связки плоскостей.

Общее уравнение плоскости

Рассмотрим общее уравнение первой степени с тремя переменными х,у и z:

A x + B y + C z + D = 0. (3.21)

Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например В ≠ 0, перепишем уравнение (3.21) в виде

A (x - 0)+ B (y + D/B) + C (z - 0) = 0.

Сравнивая данное уравнение с уравнением (3.20), видим, что это уравнение является уравнением плоскости с нормальным вектором = (А,В,С), проходящей через точку М₁( 0, - (D/B), 0).

Итак, уравнение (3.21) определяет в системе координат Охyz некоторую плоскость. Уравнение (3.21) называется общим уравнением плоскости.

Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдём уравнение плоскости π , проходящей через три данные точки М₁(х₁,у₁,z₁), М₂(х₂,у₂,z₂), и М₃(х₃,у₃,z₃), не лежащие на одной прямой.

Возьмём на плоскости произвольную точку М(х,у,z) и образуем векторы = (х – х₁, y – y₁, z – z₁) , = (х₂ – х₁, y₂ – y₁, z₂ – z₁), = (х₃ – х₁, y₃ – y₁, z₃ – z₁). Эти векторы лежат на плоскости π , следовательно, они компланарны. Используем условие компланарности трёх векторов (их смешанное произведение равно нулю), получим ∙( ) = 0, т.е.

= 0 . (3.22)

Уравнение (3.22) есть уравнение плоскости, проходящей через три точки.

Уравнение плоскости в отрезках

Пусть плоскость отсекает на осях Ox, Oy и Oz соответственно отрезки a, b и с, т.е. проходит через три точки А(а, 0,0), В(0, b, 0) и C(0, 0, c) (см. рис. 3.12)

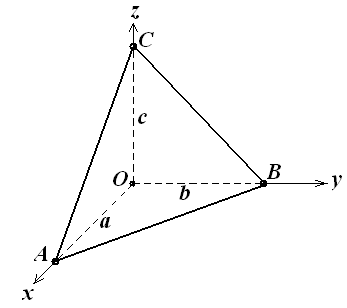
Рис. 3.12.

Подставляя координаты этих точек в уравнение (3.22), получим

= 0.

Вычислив этот определитель, имеем bcx – abc+abz+acy = 0, т.е. bcx + acy + +abz = abc или

. (3.23)

Уравнение (3.23) называется уравнением плоскости в отрезках на осях.