3. Основы аналитической геометрии
Аналитическая геометрия изучает простейшие геометрические объекты (прямые, плоскости, линии и поверхности второго порядка) средствами алгебры на основе метода координат.
3.1. Метод координат
Положение точки А в пространстве относительно некоторой точки О (полюса) можно определить с помощью вектора ОА, конец этого вектора указывает на расположение точки А в пространстве относительно точки О.
Рис. 3.1. Радиус - вектор точки А
Через точку О в пространстве проведём три взаимно перпендикулярные оси, и на каждой из них возьмём единичный вектор, направленный по этой оси (орт оси). Ось с началом отсчёта в точке О и единицей длины называется координатной осью, а упорядоченная система трёх взаимно перпендикулярных координатных осей с общим началом отсчёта О и общей единицей длины, называется прямоугольной декартовой системой координат в пространстве. В выбранной упорядоченной системе координатных осей первую ось будем называть осью абсцисс (или осью х), вторую – осью ординат (или осью у), третью – осью аппликат (или осью z).
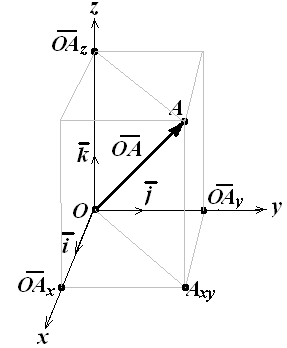
Рис. 3.2. Координатный метод задания положения точки А в пространстве.
Определение 3.1. Координатами точки в заданной прямоугольной декартовой системе координат называются проекции радиуса-вектора этой точки на координатные оси.
Координаты точки А в заданной прямоугольной декартовой системе координат (рис. 3.2) записываются в виде (x,y,z), где
x = OAx = Прх ОА , y = OAy = Прy ОА , z = OAz = Прz ОА, (3.1)
и называются соответственно абсциссой, ординатой и аппликатой точки А.
Длина вектора ОА
определяется
диагональю параллелограмма со сторонами
x,y,z,
т.е.
. (3.2)
3.2. Элементы векторной алгебры.
Геометрической моделью векторной величины является прямолинейный отрезок с выбранным на нём направлением.
Определение
3.2. Вектор
AB
–
направленный отрезок прямой, у которого
один конец (точка А) называется началом
вектора, а другой конец (точка В) – концом
вектора.
К векторам относится также и нулевой вектор, начало и конец которого совпадают.
Используя координатный метод всякий вектор в заданной упорядоченной декартовой системе координат представляется алгебраическим объектом в виде упорядоченной тройки чисел (x,y,z), где x,y,z – координаты радиус-вектора AB (точка А – начало координат), либо координаты конца В вектора AB.
Определение 3.3. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
,
где координаты точек А(0,0,0) – начало координат, В(x,y,z) (см. рис. 3.2)
Определение 3.4. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение 3.5. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Определение 3.6. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.