Список литературы

1. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. – М.: Высшая школа., 1986. – 262 с.

2. Шимони Карой. Теоретическая электротехника. М., “Мир”, 1964.774с.

3. Сухоруков В.В. Математическое моделирование электромагнитных полей в проводящих средах. М., "Энергия", 1975 – 150с.

4. Тамм И.Е. Основы теории электричества. -М.: Наука., 1989. - 504с.

5. Фальковский О. И. Техническая электродинамика: Учебник для вузов связи.- М.: Связь, 1978.- 432 с.

6. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике, т. 5-7.- М.: Мир, 1977.

7. Фальковский О. И. Методические указания к практическим занятиям по дисциплине «Электромагнитные поля и волны».- СПб.: СПбГУТ СТ «Факультет ДВО», 2000.- 65 с.

8. Петров Б. М. Электродинамика и распространение радиоволн: Учебник для вузов.- М.: Радио и связь, 2000.- 599 с.

9. Витевский В.Б., Павловская Э.А. Электромагнитные волны в технике связи. –М,; Радио и связь, 1995.

10. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров: Пер. с англ. - М.: Наука, 1984.- 832 с.

11.Никольский В.В., Никольская Т.Н. Электродинамика и распространение радиоволн: Учеб. пособие для вузов. - М.: Наука, 1989. – 544 с.

12. Годунов С.К., Рябенький В.С. Разностные схемы. М.: Наука, 1983. - 400с.

Приложение 1. Некоторые понятия векторной алгебры

Вектор – это направленный отрезок.

Длина (модуль) вектора в декартовой системе координат определяется так: , где (x₁, y₁, z₁) координаты точки начала вектора, а (x₂, y₂, z₂) - точки конца вектора.

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Векторы, лежащие в параллельных плоскостях, называют компланарными. Для равенства векторов недостаточно равенства модулей векторов, требуется еще и совпадение направлений векторов.

Вектор единичной длины называется ортом по соответствующему направлению. При линейных операциях с векторами (сложение, вычитание, умножение на число) соответствующие операции производятся с их координатами (при сложении векторов складываются их соответствующие координаты, при умножении вектора на число – умножаются нам это число).

Скалярным произведением двух векторов называют число, равное произведению модулей векторов на косинус угла между ними: (рис. 1). Скалярное произведение коммутативно. Для перпендикулярных векторов (=90) .

В декартовой системе скалярное произведение удобно вычислять через координаты векторов:

. (1)

Физический (механический) смысл скалярного произведения – работа силы по перемещению материальной точки на вектор .

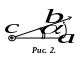
Векторным произведением двух векторов (рис. 2) называют вектор , равный по модулю произведению модулей векторов на синус угла между ними: , направленный перпендикулярно плоскости, в которой лежат и , по правилу правой тройки. Согласно этому правилу, если посмотреть со стороны конца вектора , поворот от первого вектора в векторном произведении ( ) ко второму ( ) должен происходить против часовой стрелки (рис. 2).

Векторное произведение антикоммутативно. Для коллинеарных векторов (=0) . В декартовой системе векторное произведение удобно вычислять через координаты векторов:

. (2)

Геометрически модуль векторного произведения равен площади параллелограмма, построенного на векторах и .

Физический (механический) смысл векторного произведения – момент силы в точке конца относительно точки начала вектора .

Смешанное (векторно-скалярное) произведение трех векторов – число, равное объему параллелепипеда, построенного на этих векторах:

. (3)

Двойное векторное произведение:

. (4)

Вывод дополнительных соотношений к (2.15):

или

или

14].

Приложение 2. Криволинейные системы координат

Кроме декартовой системы (ДСК) на практике также применяют криволинейные системы координат. В теории ЭМП часто используют цилиндрическую и сферическую системы координат (рис. 3), которые, как и ДСК, также являются ортогональными.

Цилиндрическая система координат (ЦСК) (r – радиус окружности в плоскости x0y,  – азимут, h – высота относительно плоскости x0y) удобна при анализе ЭМП в круглом волноводе, световоде и т. п.

Замена переменных с ДСК проводится так:

; ; ; ; . (5)

Связь между ортами ДСК и ЦСК:

; ;

; ;

. (6)

Сферическая система координат (ССК) ( – радиус сферы,  – азимут,  – угол места относительно оси z) удобна при анализе ЭМП изотропного источника и т. п. Замена переменных с ДСК проводится так:

; ;

; ;

; . (7)

Связь между ортами ДСК и ССК:

; ;

; ;

; . (8)

Связь между координатами ССК и ЦСК:

; ;

; . (9)

Связь между ортами ССК и ЦСК:

; ;

; . ( ) (10)

На плоскости (при h=0 ЦСК, =90 ССК) частным случаем обеих криволинейных систем является полярная система координат (, ).

Как видно из (3)-(8) и рис. 3 координаты ЦСК и СКК не равноправны в отличие от координат ДСК. Это приводит к тому, что при интегрировании и дифференцировании необходимо вводить корректирующие множители.

При замене переменных в определенном интеграле кроме перерасчета пределов интегрирования необходимо еще умножить подынтегральную функцию на якобиан (множитель искажений). Для тройного интеграла получаются следующие значения якобиана: r – для ЦСК и ²sin – для ССК.

. (ЦСК) (11)

. (ССК) (12)

Формулы для дифференцирования по координатам можно найти в [14].

Операции векторного анализа в ЦСК и ССК.

ЦСК:

. (13)

. (14)

. (15)

. (16)

ССК:

. (17)

. (18)

. (19)

= = . (20)