МИНОБРНАУКИ

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

"Ижевский государственный технический университет имени М.Т.Калашникова"

(ФГБОУ ВПО «ИжГТУ имени М.Т.Калашникова»)

Пособие для самостоятельной подготовки к занятиям бакалавров направления 200100.62 «Приборостроение» направления «Приборы и методы контроля качества и диагностики»

по курсу

"Теория физических полей"

Ижевск 2012

УДК 621.371; 517.949.8

Составитель: С.В. Леньков, д. т. н., профессор;

© Составитель: С.В. Леньков, д. т. н., профессор, 2012

ВВЕДЕНИЕ

Одним из наиболее важных физических полей является электромагнитное поле. С помощью методов основанных на применении электромагнитных полей осуществляется 80% неразрушающего контроля в машиностроении и 95% неразрушающего контроля в приборостроении. Диапазон частот используемых электромагнитных полей от постоянных и квазистационарных до переменных в диапазоне от радиоволнового до жесткого рентгеновского излучения, включая весь промежуточный диапазон СВЧ, видимого, инфракрасного и ультрафиолетового излучения.

Теория электромагнитного поля

1. Список, размерность (си) и соотношения физических величин используемых в электродинамике

– вектор магнитной индукции (Т);

– вектор электрической индукции (Кл/м²);

– напряженность электрического поля (В/м);

– напряженность магнитного поля (А/м);

– намагниченность вещества (А/м);

– поляризованность вещества (В/м);

–плотность потока мощности электромагнитного поля(Вт/м²);

– вектор плотности тока в проводящей среде (А/м²);

 – магнитный поток (Вб);

I – сила тока (А); U – напряжение (В);

– электрическая мощность (Вт); W – энергия (Дж);

С – емкость (Ф); L – индуктивность (Гн);

M_ik – взаимная индуктивность (Гн);

f – частота (Гц);  – циклическая частота (=2f) (рад/с).

– волновое число (1/м);  – длина волны (м);

 – постоянная затухания (1/м);  – постоянная фазы (1/м);

 – комплексный коэффициент распространения ( = +i );

– магнитная восприимчивость вещества;

– диэлектрическая восприимчивость вещества;

 – толщина скин-слоя (м) (глубина проникновения ЭМП в вещество);

– относительная диэлектрическая проницаемость

(для вакуума =1);

₀ – электрическая постоянная = 1/3610^-9 (8,85410^-11) (Ф/м);

– абсолютная диэлектрическая проницаемость ;

– относительная магнитная проницаемость (для вакуума =1);

₀ – магнитная постоянная = 410^-7 (1,25710^-6) (Гн/м);

– абсолютная магнитная проницаемость ;

– скорость света в вакууме = 310⁸ (2,9979…10⁸) (м/с);

 – удельная проводимость (См/м);

_l – линейная плотность заряда (Кл/м);

_S –плотность поверхностного заряда (Кл/м²);

 – объемная плотность заряда (Кл/м³);

– единичные вектора (орты) по соответствующие координатам декартовой системы координат (x,y,z);

- единичная нормаль к поверхности S;

- единичный касательный вектор к контуру L;

i – мнимая единица ( );

- радиус-вектор (направлен из начала координат в точку наблюдения).

2. Математическая теория поля

2.1. Определение понятия поля. Скалярные и векторные поля

Если в некоторой области V пространства R задано значение некоторой физической величины F, то говорят, что в области V задано поле этой величины.

Поля разделяются на скалярные, векторные и тензорные.

Скалярное поле – это непрерывно распределенная в каждой точке пространства некая скалярная функция с областью определения (рис. 2.1). Скалярное поле характеризуется поверхностью уровня (например, на рис. 2.1 – эквипотенциальными линиями), которую задает уравнение:.

Векторное поле – это заданное в каждой точке пространства непрерывная векторная величина с областью определения (рис. 2.2) Основной характеристикой этого поля является векторная линия, в каждой точке которой вектор поля направлен по касательной. Физическая запись силовых линий: .

Тензорное поле – это распределенная в пространстве непрерывная тензорная величина. Например, для анизотропного диэлектрика его относительная диэлектрическая проницаемость становится тензорной величиной:

.

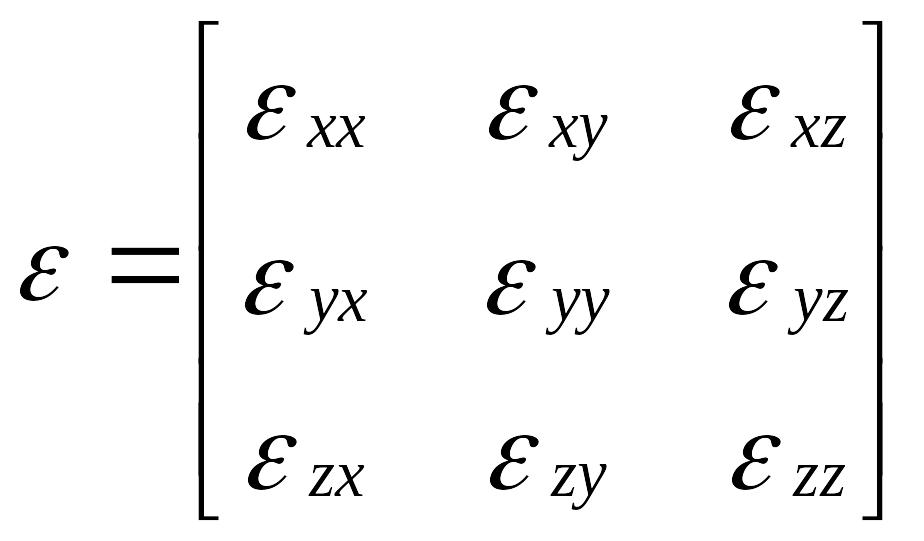2.2. Интегральные характеристики физических полей

Важные интегральные характеристики векторного поля – циркуляция и поток.

Циркуляцией (Ц) векторного поля по замкнутому контуру L называется число, равное значению криволинейного интеграла второго рода .

- циркуляция вектора . (2.1)

- поток вектора . (2.2)

Потоком (Ф) векторного поля через поверхность S (рис. 2.2) называется число, равное значению поверхностного интеграла второго рода . Знак потока зависит от выбора направления нормали к элементу поверхности dS. В случае замкнутых поверхностей принято вычислять поток, «вытекающий» наружу, поэтому выбирается внешняя нормаль.

Для анализа векторного поля в конкретной точке пространства необходимо перейти к дифференциальным характеристикам.