2. Реализация переключательных функций на мультиплексорах

Пусть требуется реализовать ПФ, зависящую от двух переменных и представленную таблицей истинности (см. табл.1).

Таблица 1.2

№ набора	x1	x0	y
0	0	0	1
1	0	1	0
2	1	0	0
3	1	1	1

Запишем обобщенную форму СДНФ для этой функции и одновременно уравнение для MS 4 1:

(1.8)

(1.9)

Очевидно полное совпадение выражений (1.8) и (1.9), из которых следует, что если логические переменные х₁ и х₀ подать на соответствующие адресные входы a₁ и a₀ MS 4 1, то на его информационные входы D₀, D₁, D₂ и D₃ нужно подать соответственно 1, 0, 0 и 1 (см. рис. 1.8).

В общем случае можно сформулировать следующее правило: если количество логических переменных n, от которых зависит реализуемая ФАЛ, совпадает с разрядностью адресной части мультиплексора, то эти переменные подаются на адресные входы мультиплексора (старшая переменная - на старший адресный вход), а на информационные входы мультиплексора MS 2ⁿ 1 – константы 0 и 1 в соответствии с таблицей истинности реализуемой ФАЛ.

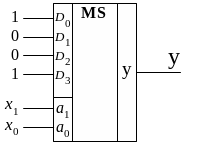
Рис. 1.8. Реализация ПФ y_MS на мультиплексоре

Попробуем реализовать теперь ПФ, зависящую от трех переменных (см. табл. 1.3), на том же MS 4 1.

Таблица 1.3

№ набора	x2	x1	x0	y
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	0
4	1	0	0	1
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

Запишем минимальную дизъюнктивную нормальную форму (МДНФ) для этой ПФ, воспользовавшись картой Вейча, представленной на рис. 1.9.

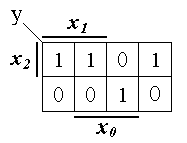
Рис. 1.9. Карта Вейча для ПФ y (табл. 1.3)

(1.10)

Преобразуем выражение (1.10) к виду, аналогичному выражению (1.8):

, (1.11)

где произведение введено для того, чтобы в выражении (1.11) были представлены все четыре конституенты единицы двух переменных х₂ и х₁.

Если сравнить выражения (1.11) и (1.9), то можно заметить их полное соответствие. Отсюда видно, что две логические переменные х₂ и х₁ нужно подать соответственно на адресные входы a₁ и a₀ MS 4 1, а информационные входы D₀, D₁, D₂ и D₃ для произвольной ФАЛ, зависящей от трех переменных, в общем случае являются функциями от третьей переменной х₀. Такими функциями являются: . Реализация данной ПФ представлена на рис. 1.10.

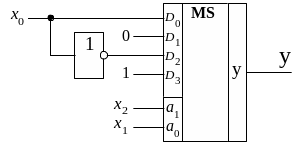
Рис. 1.10. Реализация ПФ 3 аргументов на MS 4 1

Тот же результат можно получить, если в табл. 1.3 выделить четыре группы по две строки в каждой и отделить переменную х₀ от х₂ и х₁ (см. табл. 1.4, где выделения сделаны жирными линиями).

№ набора	x2	x1	x0	y
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	0
4	1	0	0	1
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

Из табл. 1.4 видно, что переменные х₂ и х₁ образуют четыре набора, на каждом из которых функция y зависит только от одной переменной х₀, причем значения y = f(х₀) легко выявляются из этой таблицы.

Таблица 1.4

Для общего случая можно сформулировать следующее правило:

если количество логических переменных n, от которых зависит реализуемая ПФ, на единицу больше разрядности адресной части мультиплексора, то данную ПФ можно реализовать на мультиплексоре MS 2ⁿ 1 и одном инверторе.

Если распространить данный метод на реализацию ПФ, зависящей от четырех переменных, на том же MS 4 1, то, очевидно, что если две старшие переменные х₃ и х₂ подать соответственно на адресные входы a₁ и a₀, то информационные входы будут функциями двух младших переменных х₁ и х₀. Всего таких функций 16, из них шесть – вырожденные (0, 1, ), а 10 функций зависят от двух переменных, причем для реализации последних требуются восемь различных логических элементов (И, И-НЕ, ИЛИ, ИЛИ-НЕ, – элемент запрета, – элемент, реализующий функцию импликации, – элемент равнозначности и – элемент, реализующий сумму по модулю два).

Итак, данная реализация потребует кроме мультиплексора, в худшем случае, восемь различных логических элементов, поэтому ее, как правило, не рекомендуется использовать на практике.

В некоторых частных случаях ПФ, зависящую от четырех переменных, можно реализовать с использованием только одного мультиплексора MS 4 1 без каких либо логических элементов. Рассмотрим эти случаи. Пусть требуется реализовать ПФ, представленную картой Вейча (см. рис. 1.11).

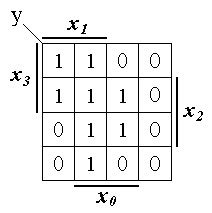
Рис. 1.11. Задание ПФ на карте Вейча

Если две старшие переменные х₃ и х₂ подать на адресные входы a₁ и a₀ MS 4 1, то информационные входы D₀, D₁, D₂ и D₃ можно представить четырьмя картами Вейча для двух переменных х₁ и х₀ (см. рис. 1.12). Эти карты являются в данном случае строками карты Вейча, представленной на рис. 1.11.

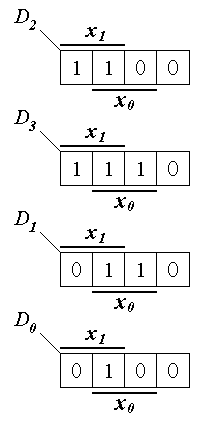
Рис. 1.12. Строки карты Вейча

Из рис. 1.12 следует: D₀ = х₁ х₀, D₁ = х₀, D₂ = х₁ + х₀ и D₃ = х₁.

Соответствующая схемная реализация представлена на рис. 1.13.

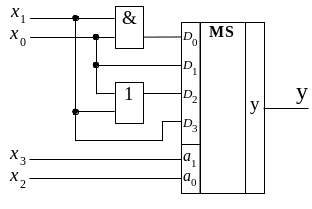
Рис. 1.13. Схемная реализация ПФ (рис. 1.11)

Подадим теперь на адресные входы a₁ и a₀ соответственно переменные х₁ и х₀, тогда информационные входы D₀, D₁, D₂ и D₃ можно представить четырьмя картами Вейча для двух переменных х₃ и х₂ (см. рис. 1.14), причем эти карты являются в данном случае столбцами карты Вейча, представленной на рис. 1.12.

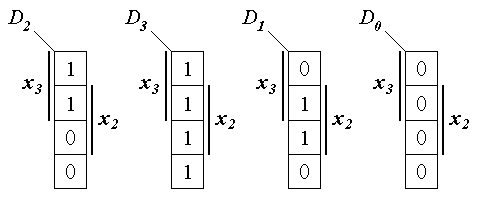
Рис. 1.14. Столбцы карты Вейча

Из рис. 1.15 следует, что D₀ = 0, D₁= х₂, D₂ = 1 и D₃ = х₃. Соответствующая реализация представлена на рис. 1.15.

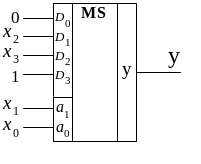
Рис. 1.15. Схемная реализация ПФ (рис. 1.11)

Сравнивая рис. 1.13 и рис. 1.15, делаем очевидный вывод о предпочтительности реализации, представленной на рис. 1.15, так как здесь не требуется никаких логических элементов.

Поиск рациональной структуры по данной методике в общем случае потребует анализа шести вариантов подачи двух различных переменных из четырех на адресные входы MS 4 1 (здесь шесть - это число различных сочетаний из четырех переменных по две). Проще рациональную структуру выявить, выполняя следующие процедуры.

Записать реализуемую ПФ в МДНФ. В нашем случае из рис. 1.11 следует:

(1.12)

Определить две переменные, наиболее часто встречающиеся в различных простых импликантах. В нашем случае это переменные х₁ и х₀, так как они встречаются по два раза, а переменные х₃ и х₂ только один раз. Именно переменные х₁ и х₀ необходимо подать на соответствующие адресные входы a₁ и a₀ MS 4 1.

Используя правило развертывания, законы дополнительности, одинарных элементов, поглощения и распределительный закон первого рода, преобразовать МДНФ к виду, когда в выражении для реализуемой ФАЛ присутствуют все четыре конституенты единицы двух переменных, выявленных на предыдущей процедуре. В нашем случае имеем:

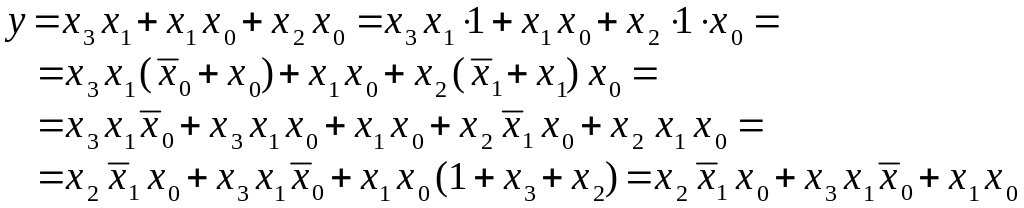(1.13)

Представим теперь выражение (1.13) в виде, аналогичном выражению (1.8):

(1.14)

Сравнивая выражения (1.9) и (1.14), выявляем, что D₀ = 0, D₁= х₂, D₂ = х₃ и D₃ =1 (см. рис. 1.15). Эту методику можно распространить и на реализацию систем двух или четырех ПФ с использованием двух- или четырехразрядных мультиплексоров, имеющих общую адресную часть. Рациональный выбор переменных, подаваемых на адресные входы мультиплексоров, определяются подсчетом общего числа каждой переменной, входящей в две или четыре функции, и в качестве адресных выбираются те переменные, которые встречаются наибольшее число раз во всех простых импликантах всех реализуемых ФАЛ.

Если использовать стробируемые MS 2ⁿ 1, имеющие три состояния выхода, то любую ФАЛ, зависящую от n + 2 переменных, легко реализовать на двух стробируемых мультиплексорах и двух инверторах. Один из инверторов используется в цепи стробирования одного из мультиплексоров, а другой на их информационных входах.

Рассмотрим пример. Пусть требуется реализовать ПФ y, представленную картой Вейча на рис. 1.16, на стробируемых мультиплексорах MS 4 1, имеющих три состояния выхода и активный уровень 0 на их стробирующих входах. Представим карту Вейча на рис. 1.16 в виде двух карт Вейча, зависящих от трех младших переменных (см. рис. 1.17).

Рис. 1.16. Задание ПФ y.

Подавая переменную х₃ непосредственно на стробирующий вход одного из мультиплексоров MS 4 1, мы реализуем функцию y₁, представленную картой Карно, показанной на рис. 1.17, и через дополнительный внешний инвертор на вход другого, мы реализуем функцию y₂, представленную картой Карно, показанной на рис. 1.17.

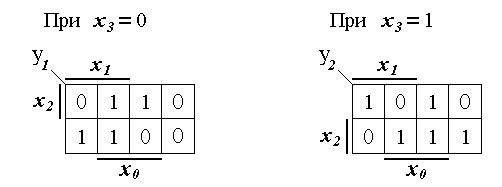
Рис. 1.17. Представление карты Вейча (рис. 1.16)

Очевидно, что y= y₁ + y₂, причем логическая операция ИЛИ реализуется здесь как монтажная операция соединением в единую цепь выходов этих двух мультиплексоров. Подавая переменные х₂ и х₁ на соответствующие адресные входы a₁ и a₀, а переменную х₀ непосредственно или через второй дополнительный внешний инвертор вместе с константами 0 и 1 на информационные входы мультиплексоров, получаем окончательную реализацию ПФ (см. рис.1.18).

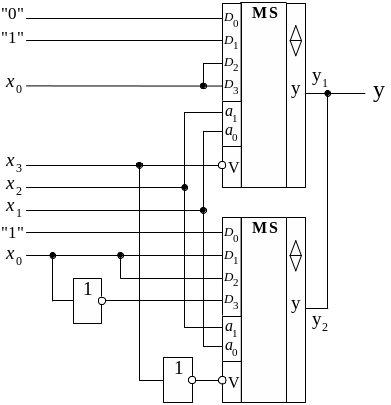
Рис. 1.18. Реализация ПФ y на двух мультиплексорах

Функции y₁ и y₂ можно реализовать по рациональным структурам, способы получения которых описаны выше.