В чому полягає суть алгоритма Фаррара-Глобера, що використовується для виявлення мультиколінеарності?
Шаг 1. Стандартизация переменных.
Элементы стандартизованных векторов рассчитываются по формулам:
,
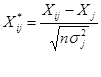i=1; n, j=1; m.
где n – число наблюдений;
m – число факторов;
σj2 – дисперсия j-го фактора.
Поскольку дисперсия рассчитывается по формуле:
,
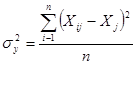то формуле для стандартизации переменных примут вид:
,
i=1; n, j=1; m.
Шаг 2. Нахождение корреляционной матрицы R (матрицы моментов стандартизованной системы нормальных уравнений).
Корелляционная матрица R определяется по формуле:
R=Х*Т·Х*,
где Х* – матрица стандартизованных переменных.
Для нахождения элементов корелляционной матрицы R последовательно используем встроенные функции Транспонирование матриц – ТРАНСП и Произведение матриц – МУМНОЖ.
Проверку вычислений следует выполнять, и используя последовательно встроенную функцию КОРРЕЛ, учитывая при этом свойства корреляционной матрицы: корреляционная матрица является симметричной, на главной диагонали расположены единицы.
Таблица 2 – Нахождение корреляционной матрицы
Транспонированная матрица стандартизированных переменных |
|
|
|
|||||||||
-0,01550062 |
-0,6665 |
-0,1085 |
-0,2325092 |
-0,171 |
0,14 |
0,32551 |
-0,0775 |
0,4495 |
0,3565 |
|||
-0,87603791 |
-0,1057 |
-0,09506 |
0,0427594 |
0,2195 |
0,269 |
0,14171 |
0,16291 |
0,2053 |
0,0357 |
|||
-0,06017464 |
0,89975 |
0,025789 |
-0,0028655 |
-0,06 |
-0,261 |
-0,2751 |
-0,0458 |
-0,189 |
-0,0315 |
|||
Корреляционная матрица |
|
|
|
|
|
|
||
|
1 |
0,222996 |
-0,8092664 |
Проверка |
1 |
0,223 |
-0,809 |
|
R |
0,223 |
1 |
-0,2146624 |
|
R |
0,223 |
1 |
-0,215 |
|
-0,8093 |
-0,21466 |
1 |
|
|
-0,8093 |
-0,2147 |
1 |
|
|
|
|
|
|
|
|
|
Коэффициент корреляции между факторами Х1 и Х2=0,223
Коэффициент корреляции между факторами Х1 и Х3=-0,8093
Коэффициент
корреляции между факторами Х2 и
Х3=-0,21466.
Вывод: на основании значения коэффициента корреляции rX2X3=-0,21466. можно сделать предварительный вывод о наличии возможной мультиколлинеарности между факторами Х2 и Х3.