1. Які задачі вирішує кореляційний аналіз?

Кореляційний аналіз вирішує два основні завдання:

Перше завдання полягає у визначенні форми зв'язку, тобто у встановленні математичної форми, в якій виражається даний зв'язок.

Це дуже важливо, тому що від правильного вибору форми зв'язку залежить кінцевий результат вивчення взаємозв'язку між ознаками.

Друге завдання полягає у вимірюванні тісноти, тобто міри зв'язку між ознаками з метою встановити ступінь впливу даного фактора на результат.

Вона вирішується математично шляхом визначення параметрів кореляційного рівняння.

Потім проводяться оцінка та аналіз отриманих результатів за допомогою спеціальних показників кореляційного методу (коефіцієнтів детермінації, лінійної і множинної кореляції і т.д.), а також перевірка суттєвості зв'язку між досліджуваними ознаками.

За допомогою кореляційного аналізу вирішують такі основні завдання: визначення типу кореляційного зв’язку між результативною ознакою і факторною; визначення «тісноти» зв’язку між ознаками, тобто наскільки жорстко результативна ознака реагує на зміну факторної; якщо результативна ознака залежить від кількох факторних, то визначення міри впливу кожної факторної ознаки.

2. Чим відрізняються коваріація та коефіцієнт кореляції?

Коефіцієнт кореляції відрізняється від коваріації тим, що він нормований за середніми квадратичними відхиленнями, тобто міра зв’язку виражається в одиницях середніх квадратичних відхилень значень ознак, є безрозмірною величиною і набуває значень від –1 до 1.

3. Чим відрізняються і яким чином розраховуються коефіцієнти парної та часткової кореляції?

Парні коефіцієнти кореляції

Парний коефіцієнт кореляції між k-м і L-м чинниками обчислюється за формулою: Він є показником тісноти лінійного статистичного зв'язку, але тільки у разі спільного нормального розподілу випадкових величин, вибірками яких є k-й і L-й чинники. За таких умов для перевірки гіпотези про рівність нулю парного коефіцієнта кореляції використовується t-статистика, розподілена згідно із законом Стьюдента з n-2 ступенями свободи. У програмі для парного коефіцієнта кореляції спочатку розраховується критичне значення t-статистики, а на його основі критичне значення коефіцієнта кореляції Якщо розрахункове значення більше критичного, то гіпотеза про рівність нулю даного коефіцієнта кореляції заперечується на відповідному рівні імовірності. Аналогічні висновки мають місце при перевірці значущості часткових коефіцієнтів кореляції.

Часткові коефіцієнти кореляції

Частковий коефіцієнт кореляції першого порядку між k-м і L-м чинниками характеризує тісноту їх лінійного зв'язку при фіксованому значенні j-го чинника. Він визначається як Він розподілений аналогічно парному коефіцієнту за таких самих передумов, і для перевірки його значеннєвості використовується t-статистика, в якій число ступенів свободи дорівнює n-3. У програмі частковий коефіцієнт кореляції розраховується в загальному вигляді, тобто за умови, що решта всіх змінних - фіксовані:

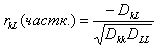Тут Dij — визначник матриці, утвореної з матриці парних коефіцієнтів кореляції викреслюванням i-го рядка і j-го стовпчика. Для кожного часткового коефіцієнта кореляції аналогічно парному розраховується t-значення для перевірки значущості коефіцієнта, а також довірчі інтервали. При цьому дисперсія z- перетвореної величини дорівнюватиме 1/(n-L-3) , де L- число фіксованих змінних (у програмі L=m-2).