Добавил:

Teana Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таврический Национальный Университет им. В.И. Вернадского

Предмет:

Экономика

Файл:

Финансовая статистика - Божко Т.Н

.pdf

Скачиваний:

Добавлен:

24.05.2014

Размер:

285.46 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Таб л и ца 2

П л ан п о гаш ени я до л га вт о рым мет о до м, мл н. руб .

	Г о д		О ста то к до лг а	Сумма	В ыпла та	Сро чна я
			на на ча ло г о да	по г а ш ения	про центо в	упла та
				до лг а
	А		1	2	3	4
	1		120	38,67	9,6	48,27
	2		81,33	41,76	6,5	48,27
	3		39,7	39,7	3,18	48,27
Сро чну ю			у п л ат у о п редел и м п о ф о рму л е:
		−	−n
y = D :		−	+ i) 1 1(
y = D :			i
			i

П о дс т ави м нео б хо ди мые данные в ф о рму л у :

		−	+	)−308 , 01 1(
y =	:		120080,	=	27 ,мл48н. ру б .
Су мма у п л ат ы п ро цент о в в ко нце п ерво го го да с о с т ави т .
D1q=120*0,08=9,6 мл н. ру б .
Размер п л ат ежа в с чет					п о гаш ени я до л га в п ерво м го ду равен:

а=у-D1*q=48,27-9,6-38,67 мл н. ру б .

Су мма у п л ат ы в ко нце вт о ро го го да с о с т ави т :

(120-38,67)*0,08=6,5 мл н. руб .

П ри	начи с л ени и	п ро цент о в
п ро и зво ди т ь	ко ррект и ро вку п ро цент
с п о с о б но с т и	ру б л я характ ери зу ет с я

денежно й еди ни цы.

нео б хо ди мо	у чи т ыват ь	и нф л яци ю ,
но й с т авки .	П адени е п о ку п ат ел ь но й
и ндекс о м п о ку п ат ел ь но й		с п о с о б но с т и

I	ед..	=	1	с пос об	покуп

		. д ен.
			I p
Ес л и наращ енная с у мма денег за n л ет с о с т авл яет						вел и чи ну S, a ди нами ка
цен характ ери зу ет с я		Ip,	т о	реал ь ная	наращ енная	с у мма п ри с о хранени и
п о ку п ат ел ь но й с п о с о б но с т и денегб у дет					равна:

~ = *SI S

ед.. . д ен.

с пос об

покупат

П у с т ь

о жи даемый с редни й т емп и нф л яци и равен r,

т о гда и ндекс цен за

го д

с о с т ави т

1+r,

и ндекс п о ку п ат ел ь но й с п о с о б но с т и

денежно й еди ни цы

З а n л ет

п ри

с о хранени и

п редл агаемо го т емп а и нф л яци и и ндекс а б у дет

1+ r

1+ i

равен

; о т с ю да

= P(

(

)

1+ r

П ри мер. Во чт о о б хо ди т с я с у мма, равная 10 т ыс . ден. ед. через10 л ет п ри

у с л о ви и , чт о

на нее

начи с л яю т с я 6 % го до вых? К ако ва б у дет ее реал ь ная

		12
п о ку п ат ел ь ная	с п о с о б но с т ь ,	ес л и п ри ро с т цен, п редп о л о жи т ел ь но б у дет

вс реднем равен 3% (п ервый вари ант ) и 8% (вт о ро й вари ант ) в го д?

Вэт о м с л у чае S=10000*(1+0,06)10=17908,43 ден. ед.

Наращ енные с у ммы с у чет о м и х о б ес ценени я с о с т авят :

061 . 0

59 .ден) . 13325ед.

(

10000=

0.03

061 . 0

08 ).ден.8295ед.

(

10000=

0.08

Таки м

о б разо м за дес ят и л ет ни й п ери о д наращ енная с у мма о б ес цени т с я

п ри мерно на 25,6% (I вари ант ) и на 53,7% (II вари ант ).

О чеви дно , чт о

ес л и

т емп и нф л яци и

равен с т авке п ро цент о в, п о

ко т о ро й

п ро и зво ди т с я наращ ени е,

т о

ро с т а реал ь но й с уммы

не п ро и зо йдет , наращ ени е

б у дет

п о л но с т ь ю

п о гл о щ ат ь с я и нф л яци ей, и

, ес л и

же r>i,

с л едо ват ел ь но S = P

т о

п ро и зо йдет

«эро зи я»

кап и т ал а,

и нф л яци я

п о гл о т и т

даже

час т ь

п ерво начал ь но й с у ммы денег.

З адача 1.

Ти п о вые задачи :

Сб ерегат ел ь ный с ерт и ф и кат но ми нал о м 9000 ру б . п о гаш ает с я через

го да п о с т авке 10%.

Треб у ет с я:

О п редел и т ь

наращ

енну ю

с т о и мо с т ь

с ерт и ф и кат а

п о

п ро с т о й

п ро цент но й и

у чет но й с т авкам.

Со с т ави т ь

п л ан

наращ ени я

п ерво начал ь но й

с т о и мо с т и

п о

п ро с т ым

п ро цент ам.

Рас с чи т ат ь

наращ

енну ю

с т о и мо с т ь

с ерт и ф и кат а

п о

с л о жно й

п ро цент но й и

у чет но й с т авкам.

Со с т ави т ь

п л ан

наращ ени я

п ерво начал ь но й

с т о и мо с т и

п о

с л о жным

п ро цент ам.

о с т ро и т ь

граф и ки

наращ ени я

с т о и мо с т и

п о п ро с т ым и

с л о жным

п ро цент ам на б азе п ро цент но й и у чет но й с т аво к.

ро анал и зи ро ват ь

до хо дно с т ь

вари ант о в

наращ ени я

с т о и мо с т и

п о зи ци й креди т о ра (держат ел я с ерт и ф и кат а) и заемщ и ка (б анка).

Реш ени е.

Наращ ени е п о п ро с т ым п ро цент ам:

а) п о п ро цент но й с т авке:

+ ni) ,SS (=1P

= 12600

ру б . ) 4 *1. 0

9000

б ) п о

у чет но й с т авке:

S =

9000

= 15000 ру б .

− nd

1− 0.1* 4

П о с л едо ват ел ь но с т ь

наращ ени я п о

п ро с т ым

п ро цент ам

о т ражена

рас чет но й т аб л и це 3.

					П л ан наращ ени я п о п ро с т ым п ро цент ам									Таб л и ца 3
					П л ан наращ ени я п о п ро с т ым п ро цент ам

П ерио д		П о про центно й ста вке									П о учетно й ста вке
на числения		Сумма						На ра щенна я			Диско нт		На ра щенна я
		про центо в						сумма					сумма
n			I=Si-P						Si		D=Sd-P			Sd
0				-					9000		-			9000
1				900					9900		1000			10000
2			1800						10800		2250			11250
3			2700						11700		3857			12857
4			3600						12600		6000			15000
Наращ ени е п о с л о жным								п ро цент ам:
а) п о п ро цент но й с т авке:
=	+ ni)n S,		S(1P						4 ==	9. +ру б .13176		) 4 *1. 0		1( 9000
б ) п о	у чет но й с т авке:
S =	P	, S =		9000			=		4. ру б .13717
S =	− d)n	, S =			− 1)		=		4. ру б .13717
	− d)n	(1			− 1)	4. 0 (1
П о с л едо ват ел ь но с т ь						наращ ени я п о				с л о жным п ро цент ам				о т ражена в
рас чет но й т аб л и це 4.
					П л ан наращ ени я п о с л о жным п ро цент ам									Таб л и ца 4
					П л ан наращ ени я п о с л о жным п ро цент ам

П ерио д		П о про центно й ста вке									П о учетно й ста вке
на числения		Сумма						На ра щенна я			Диско нт		На ра щенна я
		про центо в						сумма					сумма
N			I=Si-P						Si		D=Sd-P			Sd
0				-					9000		-			9000
1				900					9900		1000			10000
2			1890						10890		2111,1			11111,1
3			2979						11979		3345,7			12345,7
4			4176,9						13176,9		4717,4			13717,4

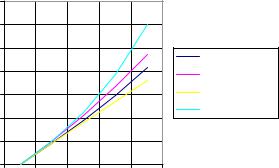
С п о зи ци й креди т о ра и заемщ и ка выго днее наращ ени е п ро цент о в п о п ро с т о й и с л о жно й у чет но й с т авкам (ри с . 1).

	16000
	15000
	14000				Si (с ложый)
.	13000				Si (с ложый)
.	13000				Sd (с ложный)
S руб	12000				Si (прос той)
	11000				Sd (прос той)
	11000
	10000
	9000
	1	2	3	4	5
			Г оды

Ри с . 1. Граф и кнаращ ени я с т о и мо с т и п о п ро с т ым и с л о жным п ро цент ам.

З адача 2.
П ро дает с я о б л и гаци я, п о гаш аемая п о с т о и мо с т и				5 т ыс . руб . через5 л ет с о
с т авко й 8%.
Треб у ет с я:
1.	о п редел и т ь	ди с ко нт ну ю	(п ро дажну ю ) цену	о б л и гаци и	п о	п ро с т о й
п ро цент но й и у чет но й с т авкам.
2.	Со с т ави т ь п л ан ди с ко нт и ро вани я п о п ро с т ым п ро цент ам п о го дам.
3.	О п редел и т ь	ди с ко нт ну ю	(п ро дажну ю ) цену	о б л и гаци и	п о	с л о жно й
п ро цент но й и у чет но й с т авкам.
4.	Со с т ави т ь п л ан ди с ко нт и ро вани я п о с л о жным п ро цент ам п о го дам.
5.	П о с т ро и т ь граф и кди с ко нт и ро вани я п о п ро с т ым и с л о жным п ро цент ам
на б азе п ро цент но й и		у чет но й с т аво к.
6.	П ро анал и зи ро ват ь до хо дно с т ь вари ант о в ди с ко нт и ро вани я с					п о зи ци и
креди т о в (держат ел я о б л и гаци и ) и			заемщ и ка (эми т ент а о б л и гаци и ).

Реш ени е. Ди с ко нт и ро вани е п о п ро с т ым п ро цент ам:

а) п о п ро цент но й с т авке: P =

б ) п о у чет но й с т авке:	d =

П о с л едо ват ел ь но с т ь ди с ко нт
рас чет но й т аб л и це 5.

S	, P =		5000	=	4.	3571
1+ n *i		1+ 5 * 0.08			ру б .
− nd P)	P S(1				==3000	− ) 08 *. 0 5 1(	5000
,	d					ру б .

и ро вани я п о п ро с т ым п ро цент ам о т ражена в

			15
					Таб л и ца 5
		П л ан ди с ко нт и ро вани я п о п ро с т ым п ро цент ам

Ч исло	лет	П о про центно й ста вке		П о учетно й ста вке
по г а ш ения		Диско нтна я	Диско нт	Диско нтна я	Диско нт
		цена		цена
	n	Pi	D=S-Pi	Pd	D=S-Pd
	5	3571,4	1428,6	3000	2000
	4	3787,9	1212,1	3400	1600
	3	4032,3	967,7	3800	1200
	2	4310,3	689,7	4200	800
	1	4629,6	370,4	4600	400
	0	5000	0	5000	0

Ди с ко нт и ро вани е п о с л о жным п ро цент ам:

а) п о п ро цент но й с т авке:					Pi =		S		, Pi =	5000		=	4.	3401
а) п о п ро цент но й с т авке:					Pi =		+ i)n		, Pi =	+	)5	=	4.	3401
							+ i)n		(1	+	)5	08 . 0 (1		ру б .
			d	=		− nd )Pn		,	PS(1			5 =		4.− 3295	) 08 . 0 1( 50
б ) п о у чет но й с т авке:			d					,	d					ру б .
б ) п о у чет но й с т авке:
П	о с л едо ват ел ь но с т ь ди с ко нт и ро вани я п о с л о жным п ро цент ам о т ражена в
рас чет но й т аб л и це 6.														Таб л и ца 6
														Таб л и ца 6
		П л ан ди с ко нт и ро вани я п о с л о жным п ро цент ам

Ч исло	лет	П о про центно й ста вке								П о учетно й ста вке
по г а ш ения		Диско нтна я			Диско нт					Диско нтна я				Диско нт
		цена								цена
n		Pi				D=S-Pd					Pd			D=S-Pd
5		3401,4				1598,6					3295,4			1704,6
4		3676,5				1323,5					3582			1418
3		3968,3				1031,7					3893,4			1106,6
2		4286,9				713,3					4232			768
1		4629,6				370,4					4600			400
0		5000				0					5000			0

					16
	С	п о зи ци и креди т о ра выго днее				ди с ко нт и ро вани е п о п ро с т о й			учет но й
и л и	с л о жно й у чет но й			с т авкам.	П ри менени е		п ро цент ных с т аво к (п ро с т о й			и
с л о жно й) о б ес п ечи вает				выго дные у с л о ви я дл я заемщ и ка (ри с .2).
			6000
			5000
		.	4000
		.						Pi
		,руб	3000					Pi
			3000					Pd

		Р	2000
		Р

			1000
			0
			0	1	2	3	4	5
					годы
			Ри с 2.Ди с ко нт и ро вани е п о п ро с т ым и с л о жным п ро цент ам.
			СТА ТИ СТИ К А БА НК О В И			БА НК О ВСК О Й ДЕЯ ТЕЛ Ь НО СТИ

О дни м и знап равл ени й в деят ел ь но с т и

б анко вс ки х у чреждени й явл яет с я

о казани е

у с л у г

п о

крат ко с ро чно му

до л го с ро чно му

креди т о вани ю

п редп ри ят и й, у чреждени й, о ргани заци й и нас ел ени я.

Ст ат и с т и ка

зани мает с я с б о ро м, о б раб о т ко й и

анал и зо м

и нф о рмаци и ,

нео б хо ди мо й в у п равл ени и ф и нанс о во -креди т ным механи змо м.

С эт о й цел ь ю

о на и зу чает

о б ъ ем и

с о с т ав креди т ных рес у рс о в и

вл о жени й,

и х ди нами ку ,

эф ф ект и вно с т ь и с п о л ь зо вани я с с у д, и х о б о рачи ваемо с т ь .

Дл я характ ери с т и ки о б о рачи ваемо с т и

рас с чи т ываю т п о казат ел и :

дл и т ел ь но с т ь п о л ь зо вани я креди т о м t –

t =

;

чи с л о

о б о ро т о в креди т а n –

n =

, где

– с редни е о с т ат ки креди т а;

On – о б о ро т

креди т а п о п о гаш ени ю ;

Д – чи с л о кал ендарных дней в п ери о де.

Ес л и и с хо дная и нф о рмаци я с о держи т

данные о

выдаче с с у д, т о и в эт о м

с л у чае мо гу т

б ыт ь рас с чи т аны т е же п о казат ел и . И зэт о го выт екает , чт о

О в

, где

О n

О в – о б о ро т креди т а п о выдаче.

О т с ю да n’=n*K’, где n’ – чи с л о

о б о ро т о в

креди т а,

и с чи с л енно е

на

о с но ве о б о ро т а с с у д п о

выдаче, К ’ – ко эф ф и ци ент

с о о т но ш ени я о б о ро т а с с у д

п о

выдаче

п о гаш ени ю .

Тако е

же

с о о т но ш ени е

между

п о казат ел ями

дл и т ел ь но с т и

п о л ь зо вани я креди т о м,

и с чи с л енными

на о с но ве данных о б о ро т а

креди т а п о выдаче и п о гаш ени ю .

И ндекс ный

мет о д

мо жет

б ыт ь

и с п о л ь зо ван

и зу чени и

с ко ро с т и

о б о рачи ваемо с т и

креди т а с о во куп но с т и

о ргани заци й. Э т о

мо гу т

б ыт ь

и ндекс ы

с редни х вел и чи н:

и ндекс

с редней

дл и т ел ь но с т и

п о л ь зо вани я

креди т о м

(п еременно го

с о с т ава)

, где

åm1

åm0

m –о дно дневный о б о ро т п о

п о гаш ени ю креди т а (m =

) .

Таккак t =

т о

=t*m и , с л едо ват ел ь но ,

åt1m1

åt0 m0

= t1 : t0 ;

åm1

åm0

и зменени е с редней дл и т ел ь но с т и

п о л ь зо вани я креди т о м п о д вл и яни ем ее

и зменени я

п о

о т дел ь ны м

еди ни цам

с о во ку п но с т и

(и ндекс

п о с т о янно го

с о с т ава):

åt1m1

åt0 m1

åm1

и зменени е

с редней

дл и т ел ь но с т и

п о л ь зо вани я

креди т о м

п о д

вл и яни ем

и зменени я

у дел ь но го вес а

о дно дневно го

о б о ро т а

п о

п о гаш ени ю о т дел ь ных

еди ни ц

с о во ку п но с т и

о б щ ей

его

вел и чи не вс ей

с о во ку п но с т и

(и ндекс

с т ру кт у рны х еди ни ц):

åt0 m1

åt0 m0

åm1

åm0

' *II

Ес л и

п ри нят ь , чт о

d =

т о

вс е т ри и ндекс а п ри му т

ви д:

åm0

и ндекс п еременно го с о с т ава

åt1d1

;

åt0 d0

и ндекс п о с т о янно го с о с т ава

åt1d1

;

åt0d0

и ндекс с т ру кт у рных с дви го в

åt0 d1

åt0 d0

		18
И ндекс ный	мет о д	дает во змо жно с т ь о п редел ят ь аб с о л ю т ные

п ри ро с т ы дл и т ел ь но с т и п о л ь зо вани я креди т о м за с чет : и нди ви ду ал ь ных значени й дл и т ел ь но с т и креди т а

	å	−	å	1 0	1 1
t		−		d t=;t	dt

с т ру кт у рны х с дви го в:

d å	− å d0t =t0		0d 1t
О б щ и й аб с о л ю т ный п ри ро с т :
å	− å d0t=0t		1dt1
t	Δ+tt	t=
	d
Дл я и зу чени я о б о рачи ваемо с т и				креди т а рас с чи т ываю т и ндекс ы с реднего
чи с л а о б о ро т о в.
С эт о й цел ь ю		с т ро ят	с л еду ю щ у ю	с и с т ему и ндекс о в:

и ндекс п еременно го с о с т ава	I		=	ån1k1	:	ån0 k	0
				åk1		åk0
		n
		n
и ндекс п о с т о янно го с о с т ава	I	'		ån1k1	:	ån0 d1
	I	n =		åk1	:	åk1
				åk1		åk1
и ндекс с т ру кт у рных с дви го в	Id		=	ån0 k1	:	ån0 k		0
	Id		=	åk1	:	åk0
				åk1		åk0

и л и I		=	ån1d1	;
			ån0 d0
	n
	n
и л и I	'		ån1d1	;
и л и I	n =		ån0 d1	;
			ån0 d1
и л и Id		=	ån0 d1	,
и л и Id		=	ån0 d0	,
			ån0 d0

где

n1 и n0

– чи с л о о б о ро т о в

креди т а

с о о т вет с т венно в

о т чет но м

б ази с но м п ери о дах;

K0 –

с редни е

о с т ат ки

креди т а

п о

о т дел ь ным

гру п п ам еди ни ц

с о во куп но с т и в о т чет но м и

б ази с но м п ери о дах.

И з взаи мо с вязи

крат ко с ро чно го

креди т а

с о б о ро т ными

с редс т вами

л о ги чес ки

выт екает

задача и зу чени я

дви жени я

вл о жени й

в крат ко с ро чный

креди т во

взаи мо с вязи

о б о рачи ваемо с т ь ю

вс ех

о б о ро т ных

с редс т в, ко т о рая

реш ает с я с п о мо щ ь ю

с л еду ю щ ей и ндекс но й мо дел и :

О =К *n’*d, где

– с о во ку п ная о б о рачи ваемо с т ь

о б о ро т ных с редс т в (о т но ш ени е о б ъ ема

вал о во го наци о нал ь но го п ро ду кт а кс редни м о с т ат кам о б о ро т ных с редс т в);

–

у ро вень

вал о во го наци о нал ь но го

п ро ду кт а

на

ру б л ь

выданных

крат ко с ро чных с с у д;

n’ – ко л и чес т во

о б о ро т о в крат ко с ро чных

с с у д, рас с чи т анно е на о с но ве

данных о выдаче креди т а;

d – до л я крат ко с ро чно го креди т а в о б щ ей с у мме о б о ро т ных с редс т в.

На о с но ве

эт о й

взаи мо с вязи

мо жно

о п редел и т ь

вл и яни е

каждо го

и з

ф акт о ро в

эт о й

мо дел и

на о б щ ее

и зменени е

о б о рачи ваемо с т и

о б о ро т ных

с редс т в.

Введем с л еду ю щ и е о б о значени я:

а– уро вень вал о во го наци о нал ь но го

п ро ду кт а в рас чет е на ру б л ь о б о ро т а

крат ко с ро чных с с у д п о выдаче, ру б .;

в – чи с л о о б о ро т о в крат ко с ро чных с с у д п о выдаче;

с – до л я крат ко с ро чных с с у д в о б щ ем о б ъ еме о б о ро т ных с редс т в;

у – чи с л о о б о ро т о в о б о ро т ных с редс т в.

То гда

п ри ро с т о б о рачи ваемо с т и

о б о ро т ных

с редс т в

о б у с л о вл ен

и зменени ем:

вал о во го

наци о нал ь но го

п ро ду кт а на ру б л ь

о б о ро т а крат ко с ро чных с с у д

п о выдаче –

I( −

с ко ро с т и

о б о рачи ваемо с т и

крат ко с ро чно го креди т а –

I( − )1 =y1

* Iв

до л и

крат ко с ро чно го креди т а в о б щ ем о б ъ еме о б о ро т ных с редс т в –

I ( − )1 = y1

* в *Ic

В задачу

с т ат и с т и ки

вхо ди т

и зу чени е

дру го го

нап равл ени я

деят ел ь но с т и

б анко вс ки х

у чреждени й – с б ерегат ел ь но го

дел а.

Дл я эт о го о на

и с п о л ь зу ет

с и с т ему

о б о б щ аю щ

и х

с т ат и с т и чес ки х п о казат ел ей,

к ко т о рым

о т но с ят с я

с редни й

размер

вкл ада,

с реднеду ш ево й

вкл ад,

с ро к

хранени я

вкл адо в, чи с л о

о б о ро т о в денежны х с редс т в во

вкл адах,

ко эф ф и ци ент ы п ри л и ва

и о с едани я вкл адо в и др.

Средни й размер вкл ада п о с о во ку п но с т и

рас с чи т ывает с я п о ф о рму л е:

l =

åB

и л и

l =

ålN

åN

где

В – с у мма вкл ада;

N – чи с л о вкл адо в.

Ди нами ка с реднего

размера

вкл ада мо жет

б ыт ь

и зу чена

п о мо щ ь ю

и ндекс но го мет о да:

и ндекс п еременно го с о с т ава

ål1d1

;

ål0 d0

и ндекс п о с т о янно го

с о с т ава

ål1d1

;

ål0 d1

и ндекс с т ру кт у рных с дви го в

ål0 d1

ål

0 d0

О б щ и й аб с о л ю т ный п ри ро с т с реднего размера вкл ада

− å d0l=0l

1dl1

в т о м чи с л е п о д вл и яни ем и зменени я:

у ро вней вкл адо в п о о т дел ь ны м гру п п ам

−

1 0

d l=l

у дел ь но го вес а чи с л а вкл адо в с разл и чным у ро внем вкл ада

− å d0l =l0

0d 1l

Δ+ll

В задаче 12 ко нт ро л ь но го

задани я т реб у ет с я рас с чи т ат ь ко эф ф и ци ент ы

п ри л и ва и

о с едани я вкл адо в. И х рас чет

п ро и зво ди т с я п о ф о рму л ам:

ко эф ф и ци ент

п ри л и ва вкл адо в –

К пр

период

;

хвклад овза

Пос т упивш и

лопериод а

ад овн ан ача

О с т ат ок

ко эф ф и ци ент

о с едани я вкл адо в –

К ос

период

хвклад овза

Пос т упивш и

плен ию

д овпопос т у

О борот вкла

Э т и

ко эф ф и ци ент ы характ ери зу ю т

с ко ро с т ь ро с т а о с т ат ко в вкл адо в.

Рас чет

п еречи с л енных в данно й т еме п о казат ел ей вып о л ни т е п о задачам.

СТА ТИ СТИ К А Ф И НА НСО В П РЕДП РИ Я ТИ Я

Дл я

реш ени я

п ракт и чес ки х задач

нео б хо ди мо

и зу чи т ь

с и с т ему

с т ат и с т и чес ки х

п о казат ел ей,

характ ери зу ю щ и х

ф и нанс о вые

резул ь т ат ы

деят ел ь но с т и

п редп ри ят и й

мет о ди ку

и х

рас чет а.

В ней

с л едует

выдел и т ь

п о казат ел и п ри б ыл и

рент аб ел ь но с т и ,

разл и чаю щ и ес я мет о ди ко й рас чет а дл я

предп ри ят и й разных о т рас л ей эко но ми ки .

При б ыл ь - важнейш и й п о казат ел ь , характ ери зу ю щ и й ко нечный резу л ь т ат

деят ел ь но с т и п редп ри ят и я и ф акт о ры его ф и нанс о во й у с т о йчи во с т и . В п ро мыш л енно с т и , с т ро и т ел ь с т ве, с ел ь с ко м хо зяйс т ве вычи с л яю т нес ко л ь ко п о казат ел ей п ри б ыл и . О с но во й дл я и х рас чет а с л ужи т балан с овая прибыль пред прият ия. О на рас с чи т ывает с я п о ф о рмул е:

Пб=Пр+Ппр+Пвн ер

где Пб - б ал анс о вая п ри б ыл ь ;

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете Экономика