3.3. Расчеты с использованием пк

Уравнение линейной регрессии можно получить на ПК, используя опции Сервис – Анализ данных – Регрессия (более подробно см. раздел 7).

Например, используя данные примера 5, в результате расчетов получим следующую таблицу:

Вывод итогов

Регрессионная статистика
Множественный -квадрат Нормированный -кв Стандартная ошибка Наблюдения	0,821816 0,675382 0,567176 0,108807 9

Дисперсионный анализ

					Значимость
Регрессия Остаток Итого	2 6 8	0,147789 0,071034 0,218822	0,073894 0,011839	6,241634	0,034207

	Коэффициенты	Стандартная ошибка	-статистика	-значение	Нижнее 95%	Верхнее 95%
пересечение	5,023567	1,862928	2,696598	0,035737	0,465144	9,581991
Переменная	-0,137011	0,06299	-2,175117	0,072548	-0,291141	0,01712
Переменная	-0,00141	0,00848	-0,166266	0,873409	-0,022161	0,019341

На основании данных таблицы можно сделать такие выводы:

• множественный коэффициент ;

• уравнение множественной регрессии ;

• -статистика 6,24.

Сравнивая полученное значение с , найденным по таблице Фишера , получим, что , т.е. уравнение регрессии значимо.

• -статистика для коэффициента равна –2,1751, для коэффициента равна –0,1663;

Сравнивая , найденное по таблице Стьюдента , с -статистиками для коэффициентов и , получаем, что -статистики коэффициентов меньше . Следовательно, коэффициенты и достаточно надежны.

• доверительные интервалы для параметров уравнения регрессии:

• для коэффициента ;

• для коэффициента .

4 Мультиколлинеарность

На практике при количественной оценке параметров эконометрической модели довольно часто сталкиваются с проблемой взаимосвязи между объясняющими переменными. Если взаимосвязь довольно тесная, то оценка параметров модели может иметь большую погрешность. Такая взаимосвязь между объясняющими переменными называется мультиколлинеарностью. Мультиколлинеарность переменных приводит к смещению оценок параметров модели. Поэтому необходима проверка факторов на мультиколлинеарность.

Наиболее простой формой проверки мультиколлинеарности является анализ корреляционной матрицы. Значение парных коэффициентов корреляции свидетельствует о том, связаны между собою переменные или нет.

Составляем симметричную матрицу коэффициентов парной корреляции

. (22)

Если среди парных коэффициентов корреляции независимых переменных существуют такие, значение которых приближается или равно множественному коэффициенту корреляции, то это говорит о возможности существования мультиколлинеарности.

Но если в модели больше двух факторов, вопрос о мультиколлинеарности не может ограничиваться информацией, которая дает эта матрица. Более общая проверка предусматривает вычисление определителя матрицы R, . Вычисляем определитель матрицы .

Если , то существует полная мультиколлинеарность.

Если , то мультиколлинеарности нет.

Чем ближе к нулю, тем увереннее можно утверждать о существовании между переменными мультикоолинеарности.

Если в эконометрической модели получено малое значение параметра при большом коэффициентов деретминации и при этом -критерий существенно отличается от нуля, то это коворит о наличии мультиколлинеарности.

Наиболее полное исследование мультиколлинеарности можно осуществить на основе алгоритма Феррара-Глаубера. Этот алгоритм включает три вида статистических критериев, на основе которых проверяется мультиколлинеарность всего массива переменных ( , хи-квадрат); каждой факторной переменной со всеми другими (F-статистика) и мультиколлинеарность каждой пары факторов (t-статистика). Все эти критерии при сравнении с их критическими значениями дают возможность сделать конкретные выводы относительно наличия или отсутствия мультиколлинеарности независимых переменных.

Алгоритм метода Феррара-Глаубера.

Для исследования общей мультиколлинеарности и мультиколлинеарностью между отдельными факторами используют корреляционную матрицу

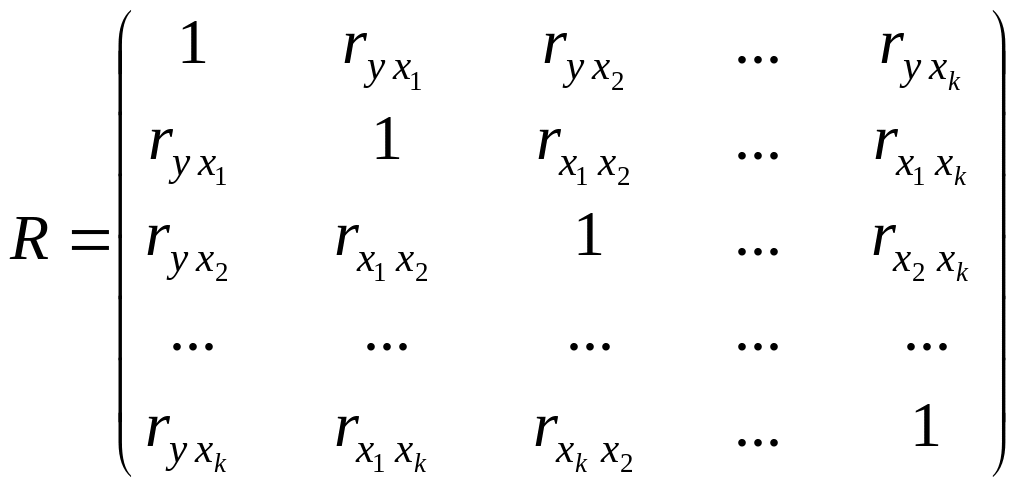, (23)

где парные коэффициенты корреляции вычисляются по формулам:

,

,

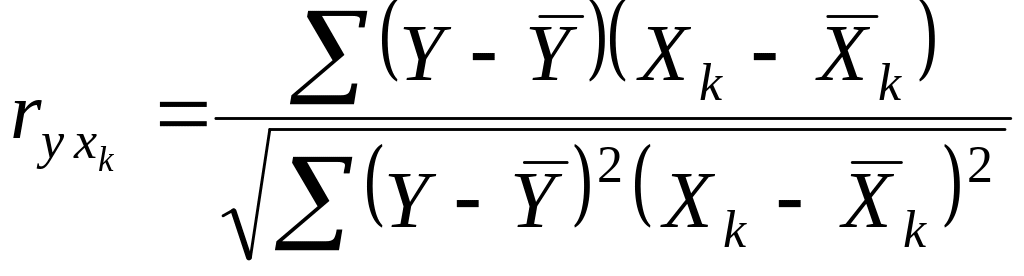где , .

Для исследования общей мультиколлинеарности используют величину критерия :

,

где – количество наблюдений, – число факторов, – определитель корреляционной матрицы .

По таблице Пирсона (приложение 3) находим .

Если , то между всеми объясняющими переменными нет общей мультиколлинеарности.

Если , то между объясняющими переменными существует общая мальтиколлинеарность.

В случае существования общей мультиколлинеарности следует определить какая из объясняющих переменных порождает мультиколлинеарность. Для этого вычисляют частные коэффициенты корреляции по формуле

, (24)

где – элементы обратной матрицы .

Критерием коллинеарности для каждой пары факторов служат величины -статистик:

.

По таблицам Стьюдента (приложение 5) находим .

Если , то между объясняющими переменными и коллинеарности нет.

Если , то между объясняющими переменными и существует значительная коллинеарность.

В случае выявления коллинеарности между парой объясняющих переменных и необходимо исключить из дальнейшего анализа переменную, которая имеет наименьшую корреляцию с показателем .

Пример 6.

Затраты на питание зависят от факторов: общие затраты, состав семьи и заработок. Надо исследовать наличие общей мультиколлинеарности по алгоритму Феррара-Глаубера.

Таблица 12

Данные для модели

Затраты на питание,	Общие затраты,	Состав семьи,	Заработок,
22	45	1,7	70
30	72	1,9	105
45	131	2	172
62	228	3,4	302
48	90	3	150
64	145	3,6	205
76	225	4,7	303
108	357	5,2	480
65	136	4,9	195
90	218	5	315

Решение.

1. Найдем корреляционную матрицу. Эта матрица симметричная. В нашем случае размера . Она имеет вид:

, (25)

где исчисляется по формуле

, (26)

где , , .

Вычислим вспомогательную таблицу:

Таблица 13

Расчет элементов корреляционной матрицы

45	1,7	70	2025	2,89	4900	76,5	3150	119
72	1,9	105	5184	3,61	11025	136,8	7560	199,5
131	2	172	17161	4	29584	262	22532	344
228	3,4	302	51984	11,56	91204	775,2	68856	1026,8
90	3	150	8100	9	22500	270	13500	450
145	3,6	205	21025	12,96	42025	522	29725	738
225	4,7	303	50625	22,09	91809	1057,5	68175	1424,1
357	5,2	480	127449	27,04	230400	1856,4	171360	2496
136	4,9	195	18496	24,01	38025	666,4	26520	955,5
218	5	315	47524	25	99225	1090	68670	1575
1647	35,4	2297	349573	142,16	660697	6712,8	480048	9327,9

В нашем случае число испытаний равно 10. Из таблицы 13 имеем:

Рассчитаем средние квадратичные отклонения:

Рассчитанные значения подставим в формулу (23):

Для данной задачи корреляционная матрица (25) имеет вид:

Элементы этой матрицы характеризуют тесноту связи между факторами.

В нашем случае Между каждой парой факторов существует определенная связь.

2. Найдем определитель корреляционной матрицы по формуле (27):

(27)

В нашем случае получим такие результаты:

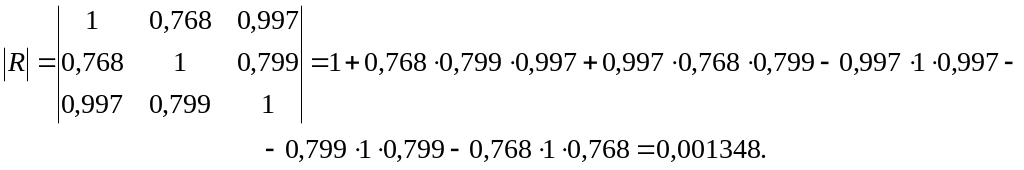
Значение определителя свидетельствует о наличии значительной мультиколлинеарности.

3. Найдем - статистику по формуле (28):

(28)

В нашем случае число испытаний число факторов , поэтому формула (28), имеет вид:

При степени свободы и уровне значимости находим по таблице (приложение 3) критическое значение .

Если , то мультиколлинеарность существует, в противном случае, то есть при мультиколлинеарность отсутствует.

В нашем случае поскольку ( ), то можем считать, что мультиколлинеарность присутствует. Поэтому один из факторов следует исключить, а именно , так как он в меньшей степени влияет на .