7. Компьютерная поддержка расчетов в пакете Excel
Использование опции Мастер функций
Опцию
Мастер
функций
можно вызвать путем нажатия на панели
инструментов кнопки
.
В результате появится окно Мастер
функций,
изображенное на рисунке 2:
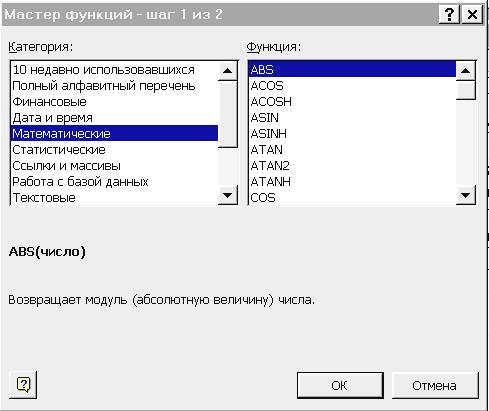
Рис.2
С
помощью клавиш прокрутки можно выбрать
какую-либо из приведенных функций.
Описание функции, если в этом есть
необходимость, можно получить при
нажатии кнопки
. С помощью этой опции можно вычислить
значение определителя, найти произведение
матриц, обратную матрицу.
7.1.1. Нахождение определителя
Пример
10.
Найти значение определителя
Алгоритм вычислений будет таким:
а) В электронную таблицу (лист 1) вносим все элементы определителя В результате получим таблицу, изображенную на рисунке 3:
Рис.3
б) Активизируем любую ячейку, например А5 – в ней будет располагаться значение определителя.
в) На панели инструментов нажимаем кнопку .
г) В появившемся окне Мастер функций выбираем Математические.
д) В окне Функция выбираем МОПРЕД.
е)
Нажимаем кнопку
.
В результате появится окно, изображенное на рисунке 4
Рис.4
ж) Активизируем Массив (установить стрелку мыши в окне и нажать левую клавишу).
з) Выбираем ячейку А1 и при нажатой левой клавише мыши передвигаемся к ячейке С3.
Номера ячеек, из которых будут взяты исходные данные, автоматически заносятся в окно Массив.
и) Нажимаем кнопку .
В результате в ячейке А5 появится результат вычислений среднего значения определителя – 0,230556.
7.1.2. Нахождение обратной матрицы
Пример
11.
Найти обратную к матрице
Алгоритм действий будет следующим:
а) Вводим матрицу на Лист 1.
В результате получим таблицу, изображенную на рисунке 5:
Р ис.5
б)
Активизируем массив размером 3
3,
например Е1:G3 – здесь будет располагаться
обратная матрица
в) На панели инструментов нажмем кнопку .
г) В появившемся окне Мастер функций выбрать Математические.
д) В окне Функция выбираем МОБР.
е) Нажимаем кнопку .
В результате появится окно, изображенное на рисунке 6.
Рис. 6
ж) Активизируем Массив (установить стрелку мыши в окне и нажать левую клавишу).
з) Выбираем ячейку А1 и при нажатой левой клавише мыши передвигаемся к ячейке С3.
Номера ячеек, из которых будут взяты исходные данные, автоматически заносятся в окно Массив.
и) Нажимаем комбинацию кнопок Ctrl+Shift+Enter .
В результате в массиве Е1:G3 появится результат: обратная матрица, изображенная на рисунке 7:
Р
ис.
7
7.1.3. Нахождение произведения матриц
Пример
12.
Найти произведение матрицы
на матрицу
Алгоритм решения реализуется следующим образом:
а) Вводим матрицы на Лист 1.
В результате получим таблицы в окне электронной таблицы Excel, изображенную на рисунке 8:
Рис.8
б) Активизируем массив размером 2 3, например H1:I3.
в) На панели инструментов нажимаем кнопку .
г) В появившемся окне Мастер функций выбираем Математические.
д) В окне Функция выбираем МУМНОЖ.
е) Нажимаем кнопку .
В результате появится окно, изображенное на рисунке 9
Рис. 9
ж) Активизируем Массив 1 (установить стрелку мыши в окне и нажать левую клавишу).
з) Выбираем ячейку А1 и при нажатой левой клавише мыши передвигаемся к ячейке С4.
и) Активизируем Массив 2 (установить стрелку мыши в окне и нажать левую клавишу).
к) Выбираем ячейку Е1 и при нажатой левой клавише мыши передвигаемся к ячейке F3.
Номера ячеек, из которых будут взяты исходные данные, автоматически заносятся в окна Массив 1 и Массив 2.
л) Нажимаем комбинацию кнопок Ctrl+Shift+Enter .
В результате в массиве H1:I3 появится матрица, представляющая собой произведение исходных матриц, изображенная на рисунке 10:
Р
ис.
10