Вспомогательные расчеты
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 |
3 |
1 |
4 |
7 |
5 |
6 |
10 |
8 |
9 |
Для каждого элемента второго ряда подсчитываем число рангов, которые его превосходят и расположены за ним. Подытоживая эти числа, получаем величину . В нашем случае она равняется
= 8+7+7+6+3+4+3+0+1 = 39.
Коэффициент ранговой корреляции Кендалла находим по формуле (31):
.
(31)
В
нашем случае формула (31) имеет вид
.
Рассчитанный коэффициент подтверждает вывод, сделанный раньше: между экспертами существует высокая согласованность мнений о влиянии факторов.
б) Значимость коэффициента Кендалла проверяем, используя критическую точку, которую находят по формуле (32):
,
(32)
где
– критическое значение, которое найдем
по таблице функции Лапласа из равенства:
.
В
нашем случае
,
тогда
,
поэтому
,
найденное по формуле (32) равняется
.
Поскольку
,
то ранговая связь между факторами
является существенной, коэффициент
Кендалла заслуживает доверия, а выводы
о влиянии факторов справедливы.
Б) Случай многих экспертов
Пример 8.
Представители 10 предприятий провели ранжирование 10 показателей, которые влияют на коммерческую работу. Наибольшее значение присваивалось наиболее значительному показателю. Необходимо провести эконометрический анализ результатов ранжирования.
Факторы
Эксперты |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
6 |
4 |
10 |
3 |
2 |
8 |
9 |
1 |
7 |
5 |
2 |
5 |
4 |
9 |
1 |
3 |
10 |
8 |
2 |
6 |
7 |
3 |
6 |
3 |
9 |
5 |
2 |
8 |
10 |
1 |
4 |
7 |
4 |
7 |
1 |
10 |
6 |
3 |
9 |
8 |
2 |
4 |
5 |
5 |
7 |
6 |
10 |
5 |
2 |
8 |
9 |
3 |
1 |
4 |
6 |
8 |
7 |
9 |
4 |
1 |
6 |
10 |
5 |
2 |
3 |
7 |
6 |
2 |
10 |
3 |
5 |
9 |
7 |
4 |
1 |
8 |
8 |
5 |
1 |
8 |
4 |
2 |
10 |
9 |
3 |
7 |
6 |
9 |
2 |
5 |
10 |
1 |
3 |
8 |
9 |
4 |
6 |
7 |
10 |
7 |
5 |
9 |
4 |
2 |
6 |
10 |
1 |
8 |
3 |
|
59 |
38 |
94 |
37 |
25 |
82 |
89 |
26 |
46 |
55 |
Решение.
Вычисление суммы рангов для всех показателей позволяет сделать следующий вывод: по мнению всех экспертов, самое значительное влияние на коммерческую деятельность осуществляют 3, 7 , 6 и 1 факторы, наименьшее влияние – 5, 8, 2 и 4 факторы.
Меру согласованности мнений экспертов проверим с помощью коэффициента конкордации, который находят по формуле 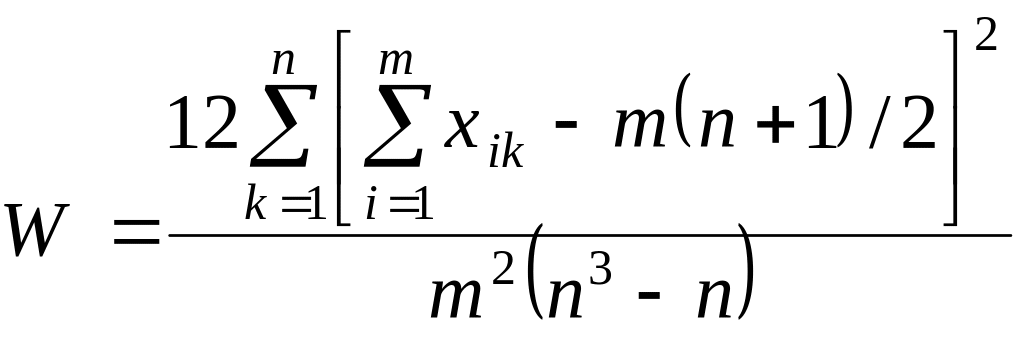(33):
,
(33)
где
– количество экспертов,
– количество факторов,
– сумма рангов по каждому фактору.
В
нашем примере
.
Надо подчеркнуть, что согласованность мнений десяти экспертов достаточно высокая.
Оценка значимости коэффициента конкордации проводится следующим образом:
рассчитывают
;по таблице (приложение 3) находят критическое значение
;
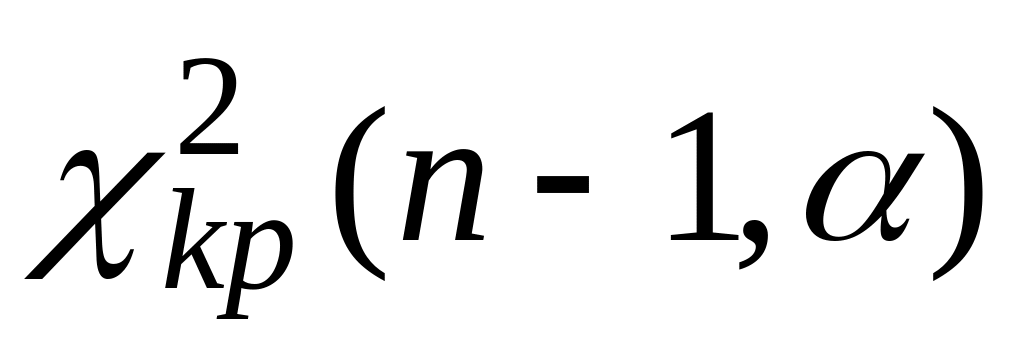сравнивают фактическое и критическое значения.
Для
рассмотренного примера имеем:
.
По
и
находим в таблице (приложение 3)
=16,92.
Мы
видим, что
значительно превышает критическую
величину, из чего следует, что коэффициенту
конкордации нужно доверять и что имеет
место достаточно высокая корреляционная
зависимость рассматриваемых факторов.
Замечание
1.
Необходимо помнить, что
,
,
.
Чем ближе эти коэффициенты к 1, тем
сильнее согласованность мнений экспертов.
Чем ближе они к нулю, тем она более
слабая.
Замечание 2. Если одни и те же факторы анализируют два эксперта, а потом большее количество экспертов, то целесообразно составить сравнительную таблицу. В частности, для рассмотренного примера имеем:
Таблица 17
Сравнительные значения
Число экспертов |
Существенные признаки |
Несущественные признаки |
2 |
3, 6, 7, 9 |
8, 4, 5, 2 |
10 |
3, 7, 6, 1 |
5, 8, 2, 4 |
Перечень несущественных факторов не изменился, их порядок стал другим. Относительно существенных факторов, то в них, кроме порядка, изменился и перечень. Ясно, что предпочтение надо отдать случаю с десятью экспертами.
Замечание 3. Из таблицы рангов можно отобрать наиболее компетентных экспертов – это те, чьи ранги более всего совпадают со средними значениями. В рассмотренном примере такими являются первый, третий и восьмой эксперты.