Питання й вправи

• У чому полягає суть видалення невидимих ліній і поверхонь?

• У якому просторі працює алгоритм Робертса?

• Для яких об'єктів приміриться алгоритм Робертса?

• Що являє собою вектор-стовпець узагальненої матриці опису багатогранника?

• Як інтерпретується вираження ( - узагальнена матриця) в алгоритмі Робертса?

• У якому просторі працює алгоритм Варнока?

• Які типи розташування багатокутника щодо вікна розглядаються в алгоритмі Варнока?

• Який із шести кроків алгоритму вирішує завдання про видалення невидимих поверхонь?

• У якому просторі працює алгоритм Вейлера-Азертона?

• У чому принципова відмінність алгоритму Вейлера-Азертона від алгоритму Варнока?

• Яке узагальнення алгоритму Вейлера-Азертона запропонував Кэтмул?

• Ким запропонований алгоритм Z-Буфера?

• У чому недоліки алгоритму Z-Буфера?

• На чому засновані методи пріоритетів?

• Для якого виду зображення розроблений метод художника?

• Для якого виду зображення розроблений метод плаваючого обрію?

• Що загального між алгоритмом порядкового сканування й методом Z-Буфера?

• У чому складається ідея методу трасування?

• Які бувають види трасування?

• Які прийоми використовуються для підвищення ефективності алгоритму трасування?

Лекція 9 проектування просторових сцен

Основні типи проекцій. Пряма й перспективна проекція. Спеціальні картографічні проекції. Екзотичні проекції земної сфери

Основні типи проекцій

У математичному змісті проекції - це перетворення крапок простору розмірності n у крапки простору розмірності меншої, чим n, або, як ще говорять, на підпростір вихідного простору. У комп'ютерній графіці розглядаються переважно проекції тривимірного простору образа на двовимірну картинну площину. Проекція тривимірного об'єкта, представленого у вигляді сукупності крапок, будується за допомогою прямих променів, що проектують, які називаються проекторами і які виходять із центра проекції, проходять через кожну крапку об'єкта й, перетинаючи картинну площину, утворять проекцію.

Певний у такий спосіб клас проекцій називають плоскими геометричними проекціями, оскільки проектування в цьому випадку виробляється на проекційну площину і як проектори використовуються прямі. Існують і інші проекції, у яких проектування здійснюється на криволінійні поверхні або ж проектування здійснюється не за допомогою прямих (такі проекції використовуються, наприклад, у картографії).

Слід зазначити, що, приводячи ілюстрації до даної глави, ми змушені використовувати ті ж самі проекції, методи побудови яких збираємося описати. Хочеться сподіватися, що матеріал через це не буде виглядати більше неясним, чим при відсутності малюнків.

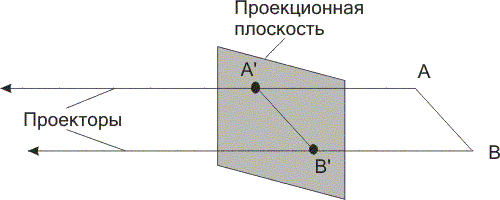
Рис. 9.1.  Проекція паралельним пучком променів

Рис. 9.2.  Центральна проекція

Плоскі геометричні проекції підрозділяються на два основних класи: центральні й паралельні. Розходження між ними визначається співвідношенням між центром проекції й проекційною площиною. Якщо відстань між ними звичайно, то проекція буде центральної, якщо ж воно нескінченно, то проекція буде паралельною. Паралельні проекції названі так тому, що центр проекції нескінченно вилученийі й всі проектори паралельні. При описі центральної проекції ми явно задаємо її центр проекції, у той час як, визначаючи паралельну проекцію, ми вказуємо напрямок проектування. На мал. 9.1 і 9.2 показані дві різні проекції того самого відрізка, а також проектори, що проходять через його кінцеві крапки. Оскільки проекція відрізка сама є відрізком, те досить спроецировать одні лише кінцеві крапки й з'єднати їх.

Центральна проекція породжує візуальний ефект, аналогічний тому, до якого приводять фотографічні системи або зорова система людини, і тому використовується у випадках, коли бажано досягти певного ступеня реалістичності. Цей ефект називається перспективним укорочуванням: у міру збільшення відстані від центра до об'єкта розмір одержуваної проекції зменшується. Це, з іншого боку, означає, що хоча центральна проекція об'єктів є реалістичної, вона виявляється непридатної для подання точної форми й розмірів об'єктів: із проекції не можна одержати інформацію про відносні відстані; кути зберігаються тільки на тих гранях об'єкта, які паралельні проекційної площини; проекції паралельних ліній у загальному випадку не паралельні. Так, при центральній проекції куба в більшості випадків ми одержуємо картину, що взагалі не має паралельних відрізків.

Паралельна проекція породжує менш реалістичне зображення, оскільки відсутнє перспективне укорочування, хоча при цьому можуть мати місце різні постійні укорочування уздовж кожної з осей. Проекція фіксує щирі розміри (з точністю до скалярного множника), і паралельні прямі залишаються паралельними. Як і у випадку центральної проекції, кути зберігаються тільки на тих гранях об'єкта, які паралельні проекційної площини.