Колірний графік мко

Тривимірна природа сприйняття кольору дозволяє відображати його в прямокутній системі координат. Будь-який колір можна зобразити у вигляді вектора, компонентами якого є відносні ваги червоної, зеленої й синьої квіток, обчислені по формулах

Оскільки ці координати в сумі завжди становлять одиницю, а кожна з координат лежить у діапазоні від 0 до 1, те всі представлені в такий спосіб крапки простору будуть лежати в одній площині, причому тільки в трикутнику, що відтинається від її позитивним октантом системи координат (рис. 3.5а). Ясно, що при такому поданні вся безліч крапок цього трикутника можна описати за допомогою двох координат, тому що третя виражається через них за допомогою співвідношення

Таким чином, ми переходимо до двовимірного подання області, тобто до проекції області на площину (рис. 3.5б).

Рис. 3.5.  Тривимірний колірний простір

З використанням такого перетворення в 1931 р. були вироблені міжнародні стандарти визначення й виміру квітів. Основою стандарту став так званий двовимірний колірний графік МКО. Оскільки, як показали фізичні експерименти, додаванням трьох основних квітів можна одержати не всі можливі колірні відтінки, то в якості базисних були обрані інші параметри, отримані на основі дослідження стандартних реакцій ока на світло. Ці параметри - - є чисто теоретичними, оскільки побудовані з використанням негативних значень основних складові кольори. Трикутник основних квітів був побудований так, щоб охоплювати весь спектр видимого світла. Крім того, рівна кількість всіх трьох гіпотетичних квітів у сумі дає білий колір. Координати кольоровості будуються так само, як і в наведеній вище формулі:

При проекції цього трикутника на площину виходить колірний графік МКО. Але координати кольоровості визначають тільки відносні кількості основних квітів, не задаючи яскравості результуючого кольору. Яскравість можна задати координатою , а визначити виходячи з величин , по формулах

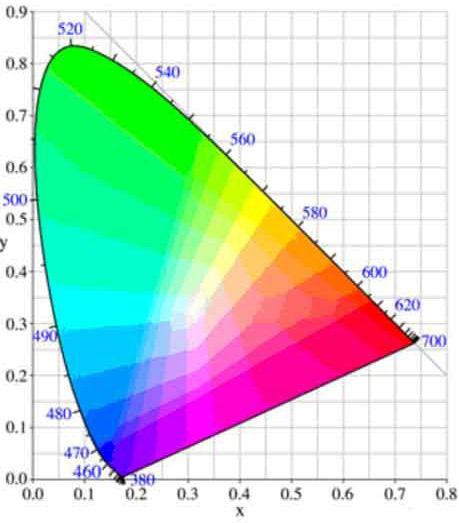
Рис. 3.6.  Колірний графік МКО. На контурі зазначені довжини хвиль у нанометрах

Колірний графік МКО наведений на рис. 3.6. Область, обмежена кривій, охоплює весь видимий спектр, а сама крива називається лінією спектральних кольорів. Числа, проставлені на малюнку, означають довжину хвилі у відповідній крапці. Крапка , що відповідає полуденному висвітленню при суцільній хмарності, прийнята в якості опорного білого кольору.

Колірний графік зручний для цілого ряду завдань. Наприклад, з його допомогою можна одержати додатковий колір: для цього треба провести промінь від даного кольору через опорну крапку до перетинання з іншою стороною кривій (кольори є додатковими друг до друга, якщо при додаванні їх у відповідній пропорції виходить білий колір). Для визначення домінуючої довжини хвилі якого-небудь кольору також проводиться промінь із опорної крапки до перетинання з даним кольором і триває до перетинання з найближчою крапкою лінії кольорів.

Для змішання двох квітів використовуються закони Грассмана. Нехай два кольори задані на графіку МКО координатами й . Тоді змішання їх дає колір . Якщо ввести позначення , то одержимо координати кольоровості суміші

Координати МКО є точним стандартом визначення кольору. Але в різних областях, що мають справу з кольором, є свій підхід до його моделювання. Зокрема, може використовуватися інший набір основних квітів. Комп'ютерна графіка опирається на систему , тому становить інтерес перехід між цими двома наборами квітів (іншими словами, перетворення координат кольоровості).