ВВЕДЕНИЕ
Контрольная работа по дисциплине «Арифметические и логические основы вычислительной техники» является одной из форм самостоятельной работы студентов, обучающихся по основной образовательной программе высшего профессионального образования по направлению подготовки 080801.65 Прикладная информатика(по областям).
Целью проведения контрольной работы является закрепление у студентов теоретических знаний по дисциплине и формирование практических навыков необходимых при изучении и разработке микропроцессорных систем управления.
Контрольная работа включает в себя четыре задания, охватывающие большинство тем дисциплины. В каждом из предложенных заданий содержится 30 вариантов исходных данных, номера которых задаются преподавателем.
Каждое задание содержит методические указания и примеры решения, что позволяет студенту самостоятельно и качественно выполнить задания контрольной работы.
Для более глубокой проработки учебного материала рекомендуется дополнительно изучить предложенную в данной методической разработке литературу или другую, уровень и задачи которой отвечают требованиям рабочей программы дисциплины.
При работе с литературой следует обратить внимание на то, что структура изложения материала в ряде учебников и учебных пособий существенно отличается друг от друга. В связи с этим при первоначальном изучении учебного материала рекомендуется последовательное прочтение всей книги. После этого следует детально проработать материал, соответствующий выполняемому заданию.
При выполнении контрольной работы необходимо соблюдать следующие требования по её оформлению:
1. на первой странице оформленной контрольной работы должны быть указаны фамилия, имя, шифр учебной группы, наименование дисциплины, номер заданного варианта;
2. выполнению каждого контрольного задания должны предшествовать постановка задачи и исходные данные, соответствующие заданному варианту. Все задания необходимо выполнять аккуратно;
3. контрольная работа обязательно должна быть зарегистрирована в деканате.
ЗАДАНИЕ 1
1. Перевести двоичное число А в шестнадцатеричную систему счисления, а из шестнадцатеричной системы – в десятичную.
2. Перевести шестнадцатеричное число С в двоичную систему счисления, а из двоичной системы – в десятичную.
3. Перевести десятичное число Е в двоичную систему счисления с абсолютной погрешностью, не превышающей 0,1.
4. Перевести десятичное число Q в двоично-десятичный код 8421, а число F из двоично-десятичного кода 8421 – в десятичную систему счисления.
Рассматриваемые числа А(2), С(16), Е(10), Q(10), F(2-10) приведены по вариантам в табл.1.
Методические указания к выполнению задания
Перевод двоичного числа в системы счисления с основаниями, кратными целой степени двойки, производится путем разбиения его на группы с соответствующим количеством разрядов, которые отсчитываются влево и вправо от точки, отделяющей целую и дробную части числа. Далее каждая группа представляется цифрой, соответствующей той системе счисления, в которую переводится число. Неполные крайние группы дополняются нулями.
Например, двоичное число 11010101.11000110 при переводе в шестнадцатеричную систему счисления разбивается на группы по четыре разряда (тетрады), а затем каждая тетрада заменяется цифрой шестнадцатеричной системы:
При обратном переводе шестнадцатеричные цифры представляются четырехразрядными группами соответствующих двоичных чисел:
Перевод чисел из двоичной и шестнадцатеричной систем счисления в десятичную систему можно производить на основе представления числа в виде полинома от основания системы, из которой переводится число. Вычисление полинома удобно выполнять по схеме Горнера, в которой количество производимых операций умножения минимально.
Преобразование полинома для вычислений по указанной схеме рассмотрим на примере перевода шестнадцатеричного числа А8В5.38С в десятичную систему счисления:
А В
С
А8В5.38С16 =10∙16 3 + 8∙ 16 2 + 11∙ 16 1 + 5∙ 16 0 + 3∙ 16 -1 + 8∙ 16 -2 + 12∙ 16 -3 =
Целая часть Дробная часть
= ((10 ∙ 16 + 8)16 + 11)16 +5 + 16 -1 (3 + 16 -1 (8 + 16 -1 ∙ 12))
Целая часть Дробная часть
В результате вычислений по преобразованному выражению получим:
А8В5.38С16 = 43189.221679610
Перевод двоичных чисел в десятичную систему счисления делается так же, как и в предыдущем примере. Отличия состоят только в значениях разрядных цифр (0 или 1) и весовых коэффициентах разрядов двоичной системы счисления.
Перевод десятичных чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления обычно производится раздельно для целой и дробной частей числа, а затем оба результата объединяются в одно число новой системы счисления.
Общее правило для перевода целого числа из системы счисления с основанием q в систему с основанием d состоит в следующем: необходимо последовательно делить переводимое число и получаемые частные на основание d до тех пор, пока не получится частное меньше основания d. Операция деления ведется в той системе счисления, из которой производится перевод числа. Целое число в новой системе счисления запишется в виде последнего частного (старшая цифра) и всех остатков деления, начиная с последнего. Например, переведем целые десятичные числа 29 и 285 соответственно в двоичную и шестнадцатеричную системы счисления:
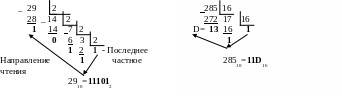
Чтобы перевести правильную дробь из системы счисления с основанием q в систему с основанием d, необходимо последовательно умножать дробь и дробные части получающихся произведений на основание d. Правильная дробь в новой системе счисления формируется в виде целых частей получающихся произведений, начиная с первого. При переводе дробей из одной системы счисления в другую можно получить дробь в виде бесконечного ряда.
Поэтому обычно задают необходимое количество разрядов m дробной части числа или абсолютную погрешность ∆ результата перевода. Считая, что абсолютная погрешность числа определяется значением единицы младшего разряда, можно записать соотношение:
∆ > d – m (1)
Так, если задана абсолютная погрешность результата перевода, то соответствующее количество разрядов числа определится из выражения:
m > log2 (1/ ∆ ) / log2 d (2)
Таблица 1
Исходные числа к выполнению задания 1
Номер варианта
|
А(2) |
С(16) |
Е(10) |
Q(10) |
F(2-10) |
1
|
1010110.011011 |
32.А4 |
17.16 |
25.492 |
0100.00000100 |
2 3 |
1000001.111010 |
88.D3 |
19.42 |
412.56 |
100101010001 |
3 |
1011000.001100 |
75.54 |
25.64 |
148.35 |
10000011.1001 |
4 |
01110.00110010 |
F1.59 |
18.14 |
18.485 |
0111.01101001 |
5 |
0101.100111011 |
64.7C |
17.22 |
78.597 |
00010101.0011 |
6 |
1110101001.101 |
B5.52 |
24.15 |
632.16 |
010110000010 |
7 |
11000111.01011 |
5A.F6 |
18.42 |
3.9781 |
0010.10010100 |
8 |
011011010.0111 |
AA.48 |
25.44 |
953.63 |
00111000.0111 |
9 |
10010011.11001 |
25.8C |
19.22 |
64.712 |
0110.01100010 |
10 |
101.0011100010 |
6B.98 |
25.15 |
853.85 |
010101000101 |
11 |
11000001010.01 |
73.B4 |
26.64 |
4.2519 |
0000.01000111 |
12 |
0110100.110001 |
E3.E4 |
27.16 |
2846.5 |
10010001.0110 |
13 |
01010.00001111 |
D9.38 |
32.22 |
936.24 |
0010.00001001 |
14 |
11101.00110001 |
96.8F |
28.42 |
15.403 |
011100010000 |
15 |
100100111.0010 |
47.39 |
30.16 |
91.865 |
01101001.0100 |
16 |
10011.01100111 |
76.7A |
31.15 |
632.17 |
01000101.0001 |
17 |
001101000.1101 |
51.C9 |
26.22 |
37.394 |
100100010110 |
18 |
1001.000111010 |
95.83 |
27.13 |
26.355 |
0100.00000011 |
19 |
0101.011100101 |
18.39 |
30.44 |
916.42 |
00010100.0011 |
20 |
11100.11111000 |
D1.35 |
28.64 |
767.51 |
0101.01011001 |
21 |
11010111.00111 |
44.F7 |
31.12 |
38.732 |
0011.10000010 |
22 |
0110.110000011 |
37.8D |
32.12 |
80.227 |
001000101000 |
23 |
100111110.1010 |
6E.22 |
16.22 |
7945.5 |
011110010101 |
24 |
1100010.011011 |
96.38 |
19.12 |
14.823 |
01000101.1001 |
25 |
101110101.1111 |
A3.64 |
17.13 |
147.65 |
01000010.0100 |
26 |
010111.0001011 |
15.16 |
25.42 |
33.797 |
0010.01100000 |
27 |
100.1001011100 |
23.8B |
33.82 |
47.632 |
0011.00000001 |
28 |
011001111.0111 |
D9.F1 |
19.16 |
307.96 |
10000.0100111 |
29 |
00110110.10001 |
55.83 |
21.34 |
22.403 |
1001.00101000 |
30 |
0110.011110111 |
31.AA |
37.43 |
344.88 |
0110.00110010 |
Например, десятичную дробь 0.3126 необходимо перевести в двоичную систему счисления с абсолютной погрешностью 0.05. Определим необходимое количество разрядов представления числа:
m > log2 (1/0.05)/log2 2= 4,3…
О
кругляя
полученный результат до ближайшего
большего целого числа, будем иметь m=5.
Следовательно, при переводе можно
ограничиться получением пятиразрядной
двоичной дроби:
Часто необходимо сохранить точность n-разрядного дробного числа при переводе его из системы счисления с основанием q в систему с основанием d.
В этом случае должно выполняться неравенство вида
q–n ≥ d –m
Отсюда необходимое количество разрядов m для сохранения точности числа в новой системе счисления определится из выражения
m ≥ n • log2 q/log2 d
Одной из модификаций двоичного и десятичного представления чисел является представление в двоично-десятичном коде 8421. Каждая десятичная цифра в таком коде представляется в виде двоичной тетрады. Указанные цифры в названии кода соответствуют значениям весовых коэффициентов разрядов двоичного числа в тетраде (23, 22, 21, 20). Максимальное двоичное число в тетраде рассматриваемого двоично-десятичного кода составляет 1001, что соответствует цифре 9 десятичной системы. Например, десятичное число 295.806 в двоично-десятичном коде 8421 представляются в виде:
295.806 10
= 0010 1001 0101 . 1000 0000 0110 2-10
2 9 5 8 0 6
При обратном переводе необходимо каждую двоичную тетраду двоично-десятичного числа заменить соответствующей десятичной цифрой.
ЗАДАНИЕ 2
Записать в 8-разрядной сетке цифрового устройства в форме с фиксированной точкой двоичные числа А и В.
Записать в 8-разрядной сетке в форме с плавающей точкой двоичное число С, выделив для мантиссы и порядка числа по четыре разряда (старшие разряды отводятся для мантиссы, младшие – для порядка числа).
Записать в 16-разрядной сетке, содержащей по восемь разрядов для мантиссы и порядка, двоичное число С в форме с плавающей точкой со смещенным порядком.
Записать в 8-разрядной сетке в прямом, обратном и дополнительном кодах двоичные числа А и В.
Выполнить в 8-разрядной сетке логический, циклический и арифметический сдвиги на R разрядов вправо и влево двоичных чисел А и В, приставив числа в прямом и дополнительных кодах.
Рассматриваемые числа А(2), В(2), С(2) и количество разрядов сдвига R приведены по вариантам в табл. 2.
Методические указания к выполнению задания
Основными представлениями чисел в разрядных сетках цифровых вычислительных устройств являются формы с фиксированной точкой (fixed-point representation) и c плавающей точкой (flotation-point representation).
В форме с фиксированной точкой могут представляться целые числа и правильные дроби. Распределение разрядов n-разрядной сетки для представления целых чисел имеет вид:
Таблица 2