Согласование экономических интересов в корпоративных структурах - Гераськин М.И

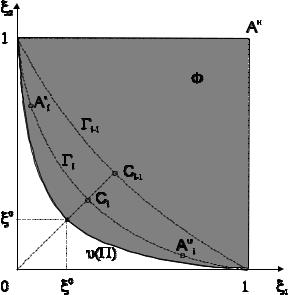
121

и коэффициенты a,b1 ,b2 вычисляются по формулам

b2 = (lnξ11 − lnξ12 )(lnξ33 − lnξ13 )− (lnξ11 − lnξ13 )(lnξ23 − lnξ13 ).

Рис. 3.1 – Формирование гипербол, аппроксимирующих множество Парето В общем случае К критериев уравнение гиперболической поверхности,

проходящей через К точек аппроксимации Аk (ξ1k ,ξ2k ,...,ξkK ),k K , имеет вид

Методика использования аппроксимирующих гипербол. С учетом свойства минимакса [187] нормализованные критерии при минимаксно- оптимальном управлении равны между собой, то есть точка, образованная сочетанием критериев при этом управлении, принадлежит биссектрисе

122

первого ортанта или, в двумерном случае, первого координатного угла.

Вследствие этого координаты центра аппроксимирующей гиперболической поверхности (точки Ci ,Ci −1 на рис. 3.1) являются приближением решения многокритериальной задачи.

Таким образом, для формирования управления, являющегося решением многокритериальной задачи, необходимо определить К векторов управления, обеспечивающих такие сочетания критериев, при которых значения (К-1) критериев фиксированы, а один критерий достигает минимума. Далее

определяются коэффициенты аппроксимирующей поверхности путем решения системы (3.13), после чего вычисляются координаты центра

аппроксимирующей поверхности по формуле

1

ξ1C = ξC2 = ... = ξCK = ξC = (a) b1+b2 +...+bK −1+1 .

Сочетание критериев в центре аппроксимирующей поверхности и соответствующий вектор управления представляют собой приближенное решение многокритериальной задачи.

Уточнение приближенного решения выполняется с помощью итерационной процедуры, при которой минимизируется критерий, максимальный для данного приближения, а значения других критериев фиксированы. Управление, полученное в результате скалярной минимизации, позволяет сформировать соответствующую аппроксимирующую поверхность, координаты центра которой являются опорным управлением на следующей итерации.

Алгоритм решения двухкритериальной задачи. В случае К=2

аппроксимирующая зависимость является гиперболой. С учетом нормализации вершина гиперболы принадлежит началу координат, так как асимптотами являются координатные оси. Линия ϑ( П ) π -оптимальных сочетаний критериев имеет вид, показанный на рис. 3.1.

Предлагается следующий алгоритм формирования минимаксно- оптимального управления:

123

н~

1)выбирается начальный закон управления u U , которому

соответствует сочетание критериев в точке Ан на рис. 3.1 (индексом "н" обозначено начальное значение);

2) определяется опорное управление, тождественное начальному ui = uн

при i = 0 (i - номер итерации) или полученному на предыдущей итерации

ui = uiC−1 при i > 0 ;

3) определяется критерий с наибольшим нормализованным значением

4)формируется управление uik' , удовлетворяющее условию

минимальности

и вычисляются координаты точки Ai' ( ξ'1i ,ξ'2i ), принадлежащей множеству

ϑ( П );

5) определяется критерий с наибольшим нормализованным значением

ξi = max ξi [ ui ] ;

k'' k k' k K

6) задается приращение Δξi и вычисляется значение критерия с номером k ¹ k'' , соответствующее этому приращению, по формуле, обратной формуле

(3.7):

~

область U дополняется ограничением

~ = { Î = ˆ ¹ }

U'' u U ,Rk [ u ] Rk ,k k'' ;

124

7)формируется управление uik'' , удовлетворяющее условию

минимальности

ивычисляются координаты точки Ai'' (ξ''1i ,ξ''2i );

8)вычисляются координаты центра гиперболы

1

ξC1i = ξC2i = ... = ξCKi = ξCi = (a)b+c+...+ z+1 ;

9) формируется управление uiC , соответствующее точке Ci (x1Ci ,xC2i ) или

Δξi+1 = 0,5Δξi и вычисления повторяются, начиная с шага 2.

Алгоритм решения многокритериальной задачи в общем случае. В

общем случае K критериев алгоритм имеет вид:

125

значение k-го критерия, полученное в результате предыдущей задачи. В каждой из K задач начальным приближением служит управление ui при k=1,

Δξi+1 = 0,5Δξi и вычисления повторяются, начиная с шага 2.

Условия сходимости алгоритма. Алгоритм позволяет определить минимаксно-оптимальное сочетание критериев ξ0 за конечное число итераций. Докажем необходимое условие сходимости алгоритма в виде следующей теоремы.

Теорема 3.1. Для заданной точности решения ε > 0 всегда найдется такой номер итерации i, что различие между минимаксно-оптимальным сочетанием критериев и решением, полученным с помощью алгоритма, не превысит этой точности, то есть

Доказательство. Для случая К=2 гиперболы, соответствующие смежным итерациям, определяются уравнениями (рис. 3.1)

Γi −1: ξ2 = fi −1(ξ1 ), Γi : ξ2 = fi (ξ1 ).

127

Так как по построению точки Аi'' верно неравенство

то при подстановке ξC2i−1 вместо f (ξ''1) неравенство (3.17) не изменит знака:

ξCi ≤ ξCi−1.

минимаксно-оптимальном управлении uО ограничивает последовательность

выполнится условие (3.16). Теорема доказана.

Особенности применения метода аппроксимации. Решение многокритериальной задачи на основе метода аппроксимации множества Парето сводится к последовательности скалярных оптимизационных задач и предусматривает: а) формирование К Парето-оптимальных управлений; б) построение в соответствии со значениями критериев при этих управлениях гиперболических поверхностей (кривые Гi ,Гi −1 на рис. 3.1),

аппроксимирующих поверхность Парето в пределах малой окрестности опорного управления; в) нахождение точки сочетания критериев,

принадлежащей аппроксимирующей поверхности и имеющей равные нормализованные значения критериев, и формирование соответствующего управления.

128

Предложенный метод позволяет определять минимаксно-оптимальное сочетание критериев ξ0 как в случае выпуклого к началу координат множества ϑ( П ), так и в невыпуклом случае, поскольку на предпоследнем шаге в невыпуклом случае ищется точка, ближайшая к C в смысле

k =1

случае алгоритм применяется в неизменном виде, но нормализованные критерии подвергаются преобразованию: ξk = βk ξk , k K .

Общие результаты предложенного метода заключаются в следующем:

–метод многокритериального выбора путем аппроксимации множества Парето по сравнению с непосредственным применением принципа максимина позволяет избежать дифференцирования функции максимума (минимума) для выбора компромиссно-оптимального управления; это преимущество особенно важно с учетом того, что функция максимума (минимума) непрерывно дифференцируема не на всей области определения;

–применение данного метода в виде формирования минимизирующей последовательности управлений сводит решение многокритериальной задачи управления к последовательности решения скалярных задач оптимизации, для которых разработаны надежные численные методы решения;

–использование предложенного метода наряду с получением конечного практически значимого результата – выбора минимаксно-оптимального управления – позволяет получить обширную информацию о структуре множества Парето; ценность этой информации заключается в том, что сопоставление минимаксно-оптимального управления с другими элементами

множества Парето является инструментом оценки качества этого управления с позиций всего комплекса критериев эффективности и служит для обоснования адекватности многокритериального выбора.

129

3.3. Метод многокритериальной оптимизации механизма корпоративного управления на основе теории графов

Рассмотрим метод, позволяющий осуществить многокритериальный

выбор путем сопоставления значений критериев эффективности различных Парето-оптимальных управлений и определения среди них управления, наиболее близкого к максиминно-оптимальному с позиций всего комплекса критериев. В основе предлагаемого метода лежат результаты теории графов.

Граф Парето-оптимальных управлений. Управление, оптимальное по критерию (3.10), может быть выбрано путем сопоставления Парето-

оптимальных управлений u*k , сформированных по критерию (3.8).

Введем в рассмотрение параметр

отражающий долю прироста (потерь) k-го критерия относительно его

максимального значения при переходе управляемой системы от управления

u*n к управлению u*m (рис. 3.2). В случае hknm > 0 управление u*m является более предпочтительным по критерию Rk по сравнению с управлением u*n , в

противном случае более предпочтительным является управление u*n .

Сформируем граф управлений [101], вершинам которого поставим в соответствие Парето-оптимальные управления u*k ,k K , а дугам – процессы

переходов от одного оптимального управления к другому в рамках процедуры сравнения управлений (рис. 3.3). Поскольку при этом сравнению подлежат все Парето-оптимальные управления, то граф управлений является связным (из любой вершины по его дугам можно перейти к другой) и полным (каждая пара вершин соединена с другой).

Определим веса дуг графа как алгебраическую сумму относительных приростов (потерь) критериев системы при переходе от управления u*n к

управлению u*m :