
Согласование интересов в матричных структурах управления - Губко М.В., Караваев А.П
..pdfУДК 519.714.3
М.В. Губко А.П. Караваев
(Институт проблем управления им. В.А.Трапезникова РАН, Москва)
Согласование интересов в матричных структурах управления
Рассмотрены задачи стимулирования, характерные для матрич- ных структур управления организационными системами: найдено
множество равновесий Нэша в двухуровневой активной системе (АС) с распределенным контролем. Для исследования коалиционных взаимодействий построена характеристическая функция и иссле-
дованы условия реализуемости коалиции всех элементов среднего звена управления. Поставлена и решена задача согласования инте- ресов различных уровней иерархии путем «внутреннего налогооб- ложения» среднего звена управления.
1.ВВЕДЕНИЕ
Внастоящее время в теории и практике менеджмента считается пер-
спективным организация управления компанией с помощью матричных структур управления (МСУ). Их суть [1] заключается в том, что на иерархи- ческую организационную структуру накладывается «горизонтальная» струк- тура проектов (см. рис. 1).

Высшее руководство
|
Проекты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Функциональная |
структура |
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Инженерное |
|
|
|
|
|
Руководство |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
управление |
|
|
|
|
|
|
НИОКР |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Менеджер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Менеджер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проекта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проекта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сотрудники |
|
|
|
|
|
|
Сотрудники |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1. Пример матричной организационной структуры
Одним из недостатков МСУ является то, что при недостаточном разде- лении полномочий между менеджерами проектов и руководителями функ- циональных подразделений возможен конфликт между ними. Представляет
интерес исследование этого конфликта с целью сравнения возможных потерь в эффективности при той или иной организации управления и определение условий максимальной эффективности управления.
В качестве аппарата исследования используется теоретико-игровое мо- делирование [2], применяемое в теории активных систем (ТАС) для изучения систем организационного управления [3].
2. ПОСТАНОВКА ЗАДАЧИ
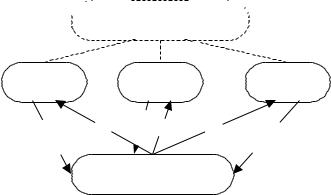
Рассмотрим активную систему (АС) [4] со структурой, изображенной на рис. 2. Центры представляют собой менеджеров проектов и руководителей функциональных подразделений, а активный элемент (АЭ) – сотрудника подразделения или подразделение в целом. Далее будет рассматриваться в основном взаимодействие центров и АЭ, роль высшего руководства будет проанализирована в последнем разделе статьи.
2











 Высшее
Высшее










 руководство
руководство
Центр 1
σ
1(
y )
...
y*
Центр i
) |
|
|
y |
* |
|
( |
||
y |
||
σ |
||
i |
|
Aктивный
элемент
...
y*
Центр n
|
) |
y |
|
( |
|
σ n |
|
Рис. 2. Модель АС с несколькими центрами
Интересы n центров описываются их функциями полезности
Фi (y) = Hi (y) −σi (y) , i Î N = {1,2,...,n},
где Hi(y) – кусочно-непрерывная функция дохода i-го центра от выбора АЭ действия y A = [0,+∞)m , σi(y) – неотрицательная функция стимулирования
АЭ i-м центром |
в зависимости от выбираемого АЭ действия. |
|
||
Интересы |
АЭ |
представлены |
функцией |
полезности |
f (y) = åσi (y) − c(y), где c(y) – положительная выпуклая возрастающая по
i N
всем компонентам вектора y функция затрат АЭ в зависимости от выбирае- мого действия y, причем существует непрерывная третья производная c'''(y) .
Все центры и АЭ имеют полную информацию о функциях Hi(y) и c(y), а также о множестве A.
Порядок функционирования системы следующий:
1.Центры одновременно сообщают АЭ функции стимулирования σi(y);
2. Если есть |
точка, в которой f (y) ³ 0 , то АЭ выбирает действие |
y* Argmax[åσi (y) − c(y)] и несет затраты c(y*), иначе он отказывает- |
|
y A |
i N |
ся от игры, и все ее участники получают нулевые выигрыши.
3.Центры получают доходы Hi(y*) и выплачивают АЭ суммы σi(y*).
3
Аксиома 1. Для функций стимулирования центров должно выполняться ба- лансовое ограничение: σ i ( y* ) ≤ Hi (y* ) , то есть центры должны иметь доста-
точно средств, чтобы оплатить АЭ обещанную сумму.
Аксиома 2. Условие «обоснованности угроз», или «условие запрета блефа»,
(1) σi ( y) ≤ Hi (y) y A, i N ,
говорящее о том, что все обещания любого центра не превышают его дохода. На протяжении всей статьи будем требовать выполнения аксиомы 1.
Если потребуется выполнение более сильной аксиомы 2 – будем оговаривать это особо.
Для завершения описания модели необходимо указать, какое действие
выберет АЭ, если множество Y (σ ) = Argmax[åσi (y) - c(y)], где
y A i N
σ = (σi ( y))i N – вектор функций стимулирования всех центров, состоит бо-
лее чем из одной точки, и АЭ должен выбрать одно действие из множества равнозначных для него действий. Для описания процесса выбора АЭ дейст- вия из множества «оптимальных» действий Y введем функцию Ψ(σ ) , из-
вестную всем центрам, которая каждому вектору функций стимулирования σ ставит в соответствие точку из соответствующего множества Y(σ).
Аксиома 3. Для функции Ψ(σ ) выполняется свойство независимости от по-
сторонних альтернатив: для любых векторов стратегий σ 1,σ 2
Ψ(σ 1 ) Y (σ 2 ) Y (σ 2 ) ÞΨ(σ 2 ) = Ψ(σ 1) ,
то есть если АЭ выбрал действие Ψ(σ 1 ) из более широкого множества
Y (σ 1) , то и из более узкого множества Y (σ 2 ) он выберет действие Ψ(σ 1 ) (если оно содержится в Y (σ 2 ) ).
4
3. ПОСТРОЕНИЕ МНОЖЕСТВА РАВНОВЕСИЙ НЭША ДЛЯ АС С НЕСКОЛЬКИМИ ЦЕНТРАМИ
Задача представляет собой анализ игры центров [4], стратегиями кото- рых является выбор функции стимулирования. Эта игра довольно сложна, так как множество стратегий представляет собой функциональное простран- ство. Хотелось бы упростить ее, введя ограничения на рассматриваемые функции стимулирования. Ниже в этом разделе доказывается теорема 2 о том, что достаточно рассматривать только функции стимулирования, отлич- ные от нуля не более чем в n точках, что редуцирует стратегию каждого цен- тра до конечномерного вектора. Затем приводится характеризация (с помо- щью системы неравенств) множества равновесий Нэша редуцированной за- дачи.
Далее значком «o » обозначается стратегия АЭ, в которой он отказыва-
ется от игры. |
Также для краткости будем обозначать (σi ( y))iÎN Þ y* тот |
||||
факт, что вектор стратегий (σi ( y))iÎN реализует точку y* , то есть, что |
|||||
|
|
ìY(σ ), max[åσi (y) - c(y)] ³ 0; |
|||
(2) y |
* |
ï |
|
y |
iÎN |
|
= í |
o |
, max[åσi (y) - c(y)] < 0. |
||
|
|
ï |
|||
|
|
î |
|
y |
iÎN |
Решением игры будем считать набор ε-равновесных по Нэшу ситуаций. Напомним, что ε-равновесием Нэша называется такой вектор стратегий σ = (σi (y))iÎN , что для любого игрока i и любой его стратегии σi (y)
(3) Фi (Ψ((σi ( y),σ −i (y)))) −Фi (Ψ(σ )) ≤ ε , где σ -i (y) = (σ j ( y)) jÎN , j ¹i [2].
Определение ε-равновесия Нэша при ε=0 переходит в определение равновесия Нэша.
Введем обозначение для всех функций стимулирования, отличных от нуля только в одной точке:
(4) P(π , y*) := ìπ , y = y*;
íî0, y ¹ y*.
5
Лемма 1. Пусть (σi ( y))iÎN – произвольный вектор стратегий центров. Тогда для центра i существует стратегия (функция стимулирования) вида (4), кото- рая при заданной обстановке σ -i (y) = (σ j ( y)) jÎN , j ¹i дает i-му центру тот же выигрыш, что и исходная стратегия σi (y) .
Для доказательства леммы 1 достаточно взять стратегию i-го центра
(5) σ~i (y) = P(σi (y* ), y* ),
где (σi ( y))iÎN Þ y* . По аксиоме 3 АЭ выберет то же действие, что и при ис- ходном векторе стратегий.
Следствие 1. Для любого центра i при фиксированной обстановке σ -i ( y)
любое достижимое с помощью произвольной стратегии значение его целевой функции Фi достижимо с помощью стратегии вида (5).
Теорема 1. Пусть (σi (y))iÎN − ε-равновесие Нэша игры центров, (σi (y))iÎN Þ y0 и выигрыш центра i в равновесии равен Фi. Тогда центр i мо-
жет в одиночку изменить свою стратегию на стратегию вида
(6) σ~i (y) = P(σi ( y0 ), y0 ) + åP(σi (y j ), y j ) ,
j ¹i
где yj находится из условия (σ j ( y) = 0,σ - j ( y)) Þ y j , и полученный набор стратегий (σ~i ( y),σ -i ( y)) будет ε-равновесием Нэша, реализующим ту же точку y0, причем выигрыш всех центров не изменится.
Доказательство теоремы 1 приведено в приложении.
Иначе говоря, для любого ε-равновесия Нэша можно найти ε- равновесие, реализующее ту же точку, что и исходное, дающее всем центрам те же выигрыши, но в котором функция стимулирования центра i отлична от нуля не более чем в n точках.
Теорема 2. Для произвольного набора чисел y0, Ф1, …, Фn, такого, что суще- ствует ε-равновесие Нэша, реализующее действие y0 и дающее центру i вы- игрыш Фi, i N , найдется ε-равновесие Нэша со стратегиями центров вида (6), реализующее действие y0, и дающее i-му игроку выигрыш Фi .
6
Доказательство теоремы 2 производится n-кратным применением тео- ремы 1.
Необходимость рассмотрения ε-равновесий Нэша обусловлена тем, что функцию Ψ(σ ) в некоторых случаях можно определить так, что множество равновесий Нэша (но не множество ε-равновесий) будет пусто. В то же вре- мя, справедливо следующее замечание:
Замечание 1. Можно положить ε=0 и считать ε-равновесия, в которых стра- тегии игроков имеют вид (5) обычными равновесиями Нэша, дополнительно указывая, что АЭ при прочих равных условиях должен выбирать действие y0. То есть переход к рассмотрению равновесий Нэша требует введения предпо- ложения о том, что при прочих равных условиях АЭ выбирает «нужное цен- трам» действие y0.
Если равновесные стратегии центров имеют вид (5), то равновесие Нэ- ша можно полностью описать набором n+1 действий y0, y1, …, yn и значения- ми функций стимулирования всех игроков в n точках (всего n2+n+1 чисел).
Таким образом, если интересоваться (что достаточно для дальнейшего изложения) только выбираемым АЭ действием y0 и выигрышами {Фi }i N всех центров в равновесии, то достаточно рассматривать только равновесия, в ко-
торых все игроки используют стратегии вида
(7)σi ( y) = P(σi0 , y0 ) + åP(σij , y j ) ,
j N
где σik ³ 0, σii = 0 "i Î N,k Î{0}U N .
Опишем множество равновесий Нэша, в которых стратегии всех цен- тров имеют вид (7).
Введем обозначения:
(8) Gi = max{Hi (y) − c(y)}, i N ,
y
выигрыш i-го центра, который он может получить в одиночку (будем счи- тать, что Gi>0, i N , то есть у каждого из центров достаточно средств, чтобы АЭ не отказался от игры);
7
(9)f = åσi0 - c(y0 ) ³ 0 ,
i N
выигрыш АЭ в равновесии.
Теорема 3. Все равновесия Нэша (в смысле Замечания 1), в которых страте- гии центров имеют вид (7), можно разбить на два типа: равновесия С-типа («сотрудничество»), в которых f = 0 (то есть центры не переплачивают АЭ за выбор нужного им действия y0), определяемые системой условий
(10) |
åσi0 |
= c(y0 ) , |
åσij |
≤ c( y j ) |
j N , |
|
|
||||||
|
i N |
|
|
|
|
i N |
|
|
|
|
|
|
|
(11) |
0 £ σ 0 |
£ H |
(y |
) - G ; |
|
|
|
|
|
|
|
||
|
i |
|
|
i |
0 |
i |
|
|
|
|
|
|
|
и равновесия К-типа («конкуренция»), определяемые системой условий |
|||||||||||||
(12) |
åσij |
− c(y j ) = f > 0 |
j {0}U N , |
|
|
||||||||
|
i N |
|
|
|
|
|
|
|
|
|
|
|
|
(13) |
max[H |
( y |
);G − f ] ≤ H |
( y |
) −σ 0 |
≤ H |
( y |
) , |
|||||
|
|
i |
i |
|
i |
|
i |
0 |
|
i |
i |
0 |
|
(14) |
0 £ Hi (y j ) -σij £ min[Hi (yj ); Hi (y0 ) -σi0 ] "i, j Î N (первое неравенство |
||||||||||||
в (14) должно выполняться, если требуется выполнение аксиомы 2). Доказательство теоремы 3 приведено в приложении.
Из доказательства теоремы 3 следует, что условия (10)-(14) являются необходимым и достаточным условием того, что набор стратегий вида (7) является равновесием Нэша.
Для исследования кооперации центров в рассматриваемой задаче по- требуется искать равновесия Нэша игры, в которой только два центра. Опре- делим множество равновесий Нэша игры при n=2:
Равновесия С-типа можно записать как
(15) c(y |
) − H |
2 |
(y |
) + G ≤ σ 0 |
≤ H |
( y |
) − G , σ 0 |
= c( y |
) −σ 0 . |
|||
0 |
|
0 |
2 |
1 |
1 |
0 |
|
1 |
2 |
0 |
1 |
|
Эта область не пуста при G1 + G2 |
≤ max[H1(y0 ) + H2 ( y0 ) − c( y0 )]. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
y0 A |
|
|
Множество равновесий К-типа задается условиями
(16)σ10 + σ 20 − c( y0 ) = σ 21 − c( y1 ) = σ12 − c(y2 ) = f > 0,
(17)max[H1(y1),G1 - f ] £ H1(y0 ) -σ10 £ H1(y0 ) , max[H2 (y2 ),G2 - f ] £ H2 (y0 ) -σ 20 £ H2 (y0 ) ,
8
(18) 0 ≤ H1 (y2 ) − c( y2 ) − f ≤ H1(y0 ) −σ10 , 0 ≤ H2 ( y1 ) − c(y1) − f ≤ H2 (y0 ) −σ 20 .
4.КООПЕРАТИВНОЕ ВЗАИМОДЕЙСТВИЕ ЦЕНТРОВ
ВАС С РАСПРЕДЕЛЕННЫМ КОНТРОЛЕМ
Для исследования возможностей кооперации центров в рассматривае- мой игре построим характеристическую функцию [2] v(S) (далее S обознача-
ет коалицию центров, непустое подмножество N), ставящую в соответствие каждой коалиции суммарный выигрыш, на который могут рассчитывать ее участники, играя совместно. Обычно [2, 6] характеристическая функция оп- ределяется как равновесный по Нэшу выигрыш коалиции S в игре с коалици- ей N\S, состоящей из всех остальных игроков. Тогда задача исследования иг- ры состоит в том, чтобы определить, какие коалиции будут образованы, и ка- ким образом доход коалиций будет распределен между их участниками.
Построение функции v(S) можно разбить на следующие этапы:
∙Определение целевой функции коалиций S и N\S и множеств их стратегий.
∙Построение множества равновесий Нэша получившейся игры двух лиц.
∙Выбор одного из равновесий в качестве основы для вычисления характе- ристической функции.
Вданной задаче целевая функция коалиции S запишется как
(19) |
ФS (y,(σi (y))i S ) = åHi (y) − åσi (y) = HS (y) −σ S (y), |
|
|
i S |
i S |
где HS (y) = åHi (y), σ S (y) = åσi (y). |
||
|
i S |
i S |
|
Соответственно, для коалиции N\S |
|
(20) |
ФN \S (y,(σ i ( y))i N \S ) = H N \S ( y) − σ N \S ( y) . |
|
Для такой игры двух лиц множество равновесий Нэша описывается ус- ловиями (15)-(18). Это множество достаточно обширно и состоит из равнове- сий двух типов – C и K. Наличие равновесий С-типа может интерпретиро- ваться как возможность совместной работы для центров. Отсутствие равно-
9
весий С-типа говорит о принципиальной невозможности кооперации цен- тров. Поэтому в дальнейшем изложении предполагается, что для произволь- ной коалиции S выполнено неравенство
(21) GS + GN \S ≤ GN
и зона С-равновесий не пуста.
Для построения характеристической функции необходимо взять одно из равновесий (или несколько, дающих коалиции S одинаковый выигрыш) за основу, то есть предположить, что центры, присоединяясь к коалиции S и оценивая перспективу совместных действий, рассчитывают именно на этот результат. Механизм выбора того или иного равновесия зависит от условий решаемой прикладной задачи. Рассмотрим некоторые возможные варианты:
1.Одним из общепринятых методов оценки выигрыша является принцип
максимального гарантированного результата [5], когда в качестве оценки берется наихудший из возможных исходов.
1.1Гарантированный результат в игре с разрешенным блефом. В игре, где блеф разрешен, всегда найдется равновесие К-типа, в котором выигрыш
|
коалиции S vГ1 |
(S) = max[min HS (y);0]. Это следующее равновесие: |
||
|
|
|
y A |
|
|
σ S0 |
= HS (y0 ) − max[min HS (y);0],σ N0 \S = HN \S |
(y0 ) − max[min HN \S (y);0], |
|
|
|
|
y A |
y A |
(22) |
σ SN \S = f (y0 ) + c(yN \S ),σ NS \S = f (y0 ) + c(yS ), |
|
||
yS |
= arg min HS |
(y), yN \S = arg min H N \S (y), |
|
|
|
|
y A |
y A |
|
|
y0 |
= arg max[HS (y0 ) + HN \S (y0 ) − c(y0 )], |
|
|
|
|
y A |
|
|
|
где f(y0) − выигрыш АЭ в точке y0. |
|
||
1.2 |
Гарантированный результат в игре с запрещенным блефом. Из (18) |
|||
|
следует, что f £ min[HS ( yN \S ) - c( yN \S ); H N \S ( yS ) - c( yS )]. |
|||
|
Тогда на основании формулы (17) можно записать условие на ФS: |
|||
|
ФS |
³ max[HS (yS );GS - HS (yN \S ) + c( yN \S );GS |
- HN \S ( yS ) + c( yS )] . |
|
|
Это выражение достигает минимума при |
|
||
(23) GS |
= HS (yS* ) + HN \S ( yS* ) − c(yS* ) = HN ( yS* ) − c( yS* ) , |
|||
|
yN \S = argmax[HS (y) − c(y)], |
|
||
|
|
y A |
|
|
10
